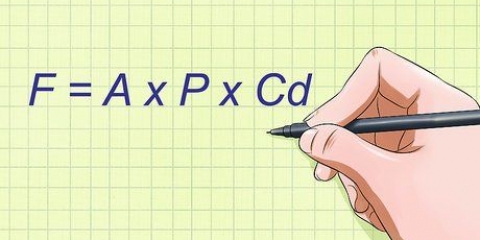Felmarginalen är en procentandel som anger hur nära resultaten av ditt urval kommer att vara det verkliga värdet av den totala populationen som diskuteras i din studie. En mindre felmarginal kommer att resultera i mer exakta svar, men att välja en mindre felmarginal kräver också ett större urval. När resultatet av en undersökning presenteras visas felmarginalen vanligtvis som en plus- eller minusprocent. Till exempel: `35 % av människorna håller med alternativ A, med en felmarginal på +/- 5 %` I det här exemplet indikerar felmarginalen i huvudsak att om hela befolkningen fick samma undersökningsfråga är du "säker" på att någonstans mellan 30 % (35 - 5) och 40 % (35 + 5) skulle hålla med om alternativ A. 
Med andra ord, om du väljer en konfidensnivå på 95 % kan du hävda att du är 95 % säker på att dina resultat ligger inom den valda felmarginalen. En högre konfidensnivå indikerar en högre grad av noggrannhet, men kräver också ett större urval. De vanligaste konfidensnivåerna är 90% säker, 95% säker och 99% säker. Att ställa in en konfidensnivå på 95 % för exemplet i felmarginalsteget innebär att du är 95 % säker på att 30 % till 40 % av den totala påverkade befolkningen håller med "alternativ A" i din undersökning. 
Extrema svar är mer benägna att vara korrekta än måttliga resultat. Om 99 % av svaren på din enkät svarar "Ja" och bara 1% "Nej", är urvalet troligen en mycket korrekt återspegling av hela populationen. Å andra sidan, om 45 % svarar "Ja" och 55% "Nej", finns det en större risk för fel. Eftersom detta värde är svårt att fastställa när man ger den faktiska undersökningen, satte de flesta forskare detta värde till 0,5 (50 %). Detta är procentandelen i värsta fall, så att hålla fast vid detta värde säkerställer att din beräknade urvalsstorlek är tillräckligt stor för att korrekt representera den totala populationen inom ditt konfidensintervall och konfidensnivå. 
Du kan beräkna z-poäng för hand, använda en online-kalkylator eller hitta din z-poäng i en z-poängtabell. Var och en av dessa metoder kan dock vara ganska komplexa. Eftersom konfidensnivåerna är ganska standardiserade, kommer de flesta forskare helt enkelt ihåg den nödvändiga z-poängen för de vanligaste konfidensnivåerna: 80 % tillförlitlighet => 1,28 z-poäng 85 % tillförlitlighet => 1,44 z-poäng 90% tillförlitlighet => 1,65 z-poäng 95% förtroende => 1,96 z-poäng 99% tillförlitlighet => 2,58 z-poäng 

Exempel: Bestäm den ideala studiestorleken för en population på 425 individer. Använd en 99 % konfidensnivå, en 50 % standardavvikelse och en felmarginal på 5 %. För 99 % konfidens bör du ha ett z-poäng på 2,58. Detta innebär att: N = 425 z = 2,58 e = 0,05 sid = 0,5 
Exempel: Provstorlek =*p(1-p)] / e / 1 + [z *p(1-p)] / e *N] =*0,5(1-0,5)] / 0,05 / 1 + [2,58 *0,5(1-0.5)] / 0,05 *425] =/ 1 + [6,6564 *0,25] / 1,0625] = 665 / 2,5663 = 259,39(svar) 

Exempel: Bestäm den erforderliga studiestorleken för en okänd population med 90 % konfidensnivå, 50 % standardavvikelse och 3 % felmarginal. För 90 % konfidens skulle z-poängen vara 1,65. Detta innebär att: z = 1,65 e = 0,03 sid = 0,5 
Exempel: Provstorlek = [z *p(1-p)] / e = [1,65 *0,5(1-0,5)] / 0,03 = [2,7225 *0,25] / 0,0009 = 0,6806 / 0,0009 = 756,22 (svar) 

Exempel: Beräkna den erforderliga studiestorleken för en population på 240 försökspersoner, med hänsyn till en felmarginal på 4 %. Detta innebär att: N = 240 e = 0,04 
Exempel: Provstorlek = N / (1 + N*e) = 240 / (1 + 240 *0,04) = 240 / (1 + 240 *0,0016) = 240 / (1 + 0,384} = 240 / (1 384) = 173,41 (svar)
Beräkna en provstorlek
Vetenskapliga studier bygger ofta på undersökningar gjorda bland en liten del av den totala befolkningen. Ditt urval måste dock ha ett minsta antal datapunkter om du vill att det korrekt ska representera förhållandena för den totala populationen det är avsett att representera. För att beräkna den nödvändiga provstorleken måste du bestämma några fasta värden och ange dem i en lämplig formel.
Steg
Del 1 av 4: Fastställande av de viktigaste värdena

1. Känn din befolkningsstorlek. Populationsstorlek hänvisar till det totala antalet datapunkter inom din population. För större studier kan du använda ett uppskattat värde istället för det exakta antalet.
- Precision har större statistisk påverkan när du arbetar med en mindre grupp. Om du till exempel vill undersöka medlemmar i en organisation eller anställda i ett litet företag, måste befolkningsstorleken vara korrekt för ett dussin personer.
- Större undersökningar tillåter större avvikelse från den faktiska populationen. Till exempel, om din demografi inkluderar alla som bor i Nederländerna, kan du uppskatta storleken till ungefär 17 miljoner människor, även om det verkliga värdet kan skilja sig med hundratusentals.

2. Bestäm din felmarginal. Felmarginal, även känd som "konfidensintervall", hänvisar till hur stor varians du vill tillåta i dina resultat.

3. Bestäm din självförtroendenivå. Konfidensnivån är nära relaterad till konfidensintervallet (felmarginal). Detta värde mäter din grad av säkerhet om hur väl ett urval representerar den totala populationen inom din valda felmarginal.

4. Ange din standardavvikelse. Standardavvikelsen anger hur stor variation du förväntar dig bland dina svar.

5. Hitta din Z-poäng. Z-poängen är ett konstant värde som ställs in automatiskt baserat på din konfidensnivå. Det indikerar `standard normalpoäng`, eller antalet standardavvikelser mellan ett valt värde och populationsmedelvärdet.
Del 2 av 4: Använda standardformeln

1. Titta på jämförelsen. Om du har en liten till medelstor befolkning och känner till alla nyckelvärden bör du använda standardformeln. Standardformeln för en provstorlek är:
- Provstorlek =*p(1-p)] / e / 1 + [z *p(1-p)] / e *N]
- N = befolkningsstorlek
- z = z-poäng
- e = felmarginal
- sid = standardavvikelse

2. Ange dina värden. Ersätt variablerna med de numeriska värden som faktiskt gäller för din specifika undersökning.

3. Utför beräkningen. Lös ekvationen med de nya siffrorna. Lösningen är din önskade provstorlek.
Del 3 av 4: Att skapa en formel för okända eller mycket stora populationer

1. Undersök formeln. Om du har en okänd eller mycket stor befolkning, måste du använda en andra formel. Om det fortfarande finns värden för resten av variablerna, använd följande ekvation: Vet att denna ekvation bara är den övre halvan av hela formeln.
- Provstorlek = [z *p(1-p)] / e
- z = z-poäng
- e = felmarginal
- sid = standardavvikelse

2. Fyll ekvationen med dina värden. Ersätt varje variabel med de numeriska värden som valts för din forskning.

3. Utför beräkningen. När du har lagt in dina siffror i formeln löser du ekvationen. Ditt svar kommer att ange önskad provstorlek.
Del 4 av 4: Att använda Slovins formel

1. Titta på formeln. Slovins formel är en väldigt generell ekvation som används när man kan uppskatta populationen men inte har någon aning om hur en viss population beter sig. Formeln beskrivs enligt följande: Vet att detta är den minst exakta formeln och som sådan den minst idealiska. Du bör bara använda den om omständigheterna hindrar dig från att bestämma en lämplig standardavvikelse och/eller konfidensnivå (vilket också hindrar dig från att bestämma din z-poäng).
- Provstorlek = N / (1 + N*e)
- N = befolkning
- e = felmarginal

2. Ange värdena. Ersätt varje variabel med de numeriska värdena som är specifika för din undersökning.

3. Utför beräkningen. Lös ekvationen med de siffror som är specifika för din forskning. Svaret du kommer fram till bör vara storleken på din forskning.
Оцените, пожалуйста статью