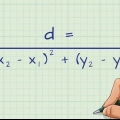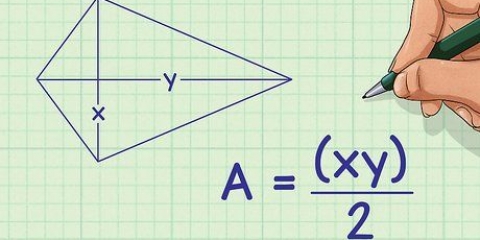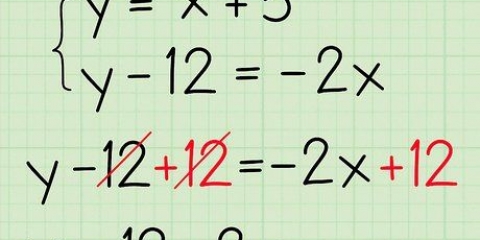Till exempel, om bredden på en rektangel är 3 cm och längden är 4 cm, skulle din formel se ut så här:  .
. 
Till exempel:




Till exempel:



Så diagonalen eller rektangeln med en bredd på 3 cm och en längd på 4 cm är 5 cm. 

Till exempel, om arean av rektangeln är 35 kvadratcentimeter, skulle din formel se ut så här:  .
. 
Till exempel:

 .
. 

Till exempel, om omkretsen av en rektangel är 24 centimeter, skulle din formel se ut så här:  .
. 
Till exempel:


 .
. 
Till exempel, om du hittade med areaformeln att  , då byter du ut värdet
, då byter du ut värdet  i omkretsformeln:
i omkretsformeln:



Till exempel:




Till exempel:




Till exempel,  blir
blir  .
. 
Till exempel ekvationen  kan lösas upp i
kan lösas upp i  .
. 
Till exempel:


OCH

 .
.
Så längden och bredden på rektangeln är 7 cm och 5 cm. 
Du använder Pythagoras sats eftersom diagonalen i en rektangel delar upp den i två kongruenta räta trianglar. Bredden och längden på rektangeln är längden på triangelns sidor; diagonalen är triangelns hypotenusa. 
Om du till exempel vet att rektangelns bredd och längd är 5 cm och 7 cm, skulle din formel se ut så här:  .
. 
Till exempel:




Till exempel:



Så diagonalen för en rektangel med en yta på 35 cm och en omkrets på 24 cm är cirka 8,6 cm. 

Du kan använda den här metoden om du känner till rektangelns omkrets, förutom att du nu använder omkretsformeln istället för areaformeln. Formeln för omkretsen av en rektangel är  , varigenom
, varigenom  är lika med rektangelns bredd, och
är lika med rektangelns bredd, och  är lika med längden på rektangeln.
är lika med längden på rektangeln. 
Till exempel, om arean av rektangeln är 35 kvadratcentimeter, skulle din formel se ut som volt:  .
. 
Till exempel om du har hittat det  , då ersätter du denna relation
, då ersätter du denna relation  i områdesformeln:
i områdesformeln:



Till exempel:




Till exempel ekvationen  kan lösas upp som
kan lösas upp som  .
. 
Till exempel:


OCH

 .
.
I det här fallet finns det ett negativt svar. Eftersom längden på en rektangel inte kan vara negativ vet du att längden måste vara 5 cm. 
Till exempel, om du vet att längden på rektangeln är 5 cm, och att förhållandet mellan sidornas längder är lika med  , sedan anger du 5 som längd i formeln:
, sedan anger du 5 som längd i formeln:




Du använder Pythagoras sats eftersom diagonalen i en rektangel delar upp den i två kongruenta räta trianglar. Bredden och längden på rektangeln är längden på triangelns sidor; diagonalen är triangelns hypotenusa. 
Om du till exempel vet att rektangelns bredd och längd är lika med 5 cm och 7 cm, ser din formel nu ut så här:  .
. 
Till exempel:




Till exempel:



Så diagonalen för en rektangel med en bredd som är 2 cm mer än dess längd och har en yta på 35 cm, är cirka 8,6 cm.
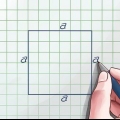
Beräkna längden på diagonalen i en rektangel
En diagonal är en rät linje som förbinder ett hörn av en rektangel med det motsatta hörnet. En rektangel har två diagonaler, var och en av samma längd. Om du vet längden på sidorna i en rektangel är det lätt att hitta längden på diagonalen med hjälp av Pythagoras sats, eftersom en diagonal delar en rektangel i två räta trianglar. Om du inte känner till längderna på sidorna, men du har andra data (som arean och omkretsen, eller förhållandet mellan sidornas längder), kan du mäta längden och bredden på sidorna med en några extra steg. hitta rektangeln och sedan använda Pythagoras sats, hitta längden och bredden på diagonalen.
Steg
Metod 1 av 3: Använd längden och bredden

1. Skriv formeln för Pythagoras sats. Formeln är  , varigenom
, varigenom  och
och  är lika med längden på sidorna i en rätvinklig triangel, och
är lika med längden på sidorna i en rätvinklig triangel, och  är lika med längden på hypotenusan i en rätvinklig triangel.
är lika med längden på hypotenusan i en rätvinklig triangel.
 , varigenom
, varigenom  och
och  är lika med längden på sidorna i en rätvinklig triangel, och
är lika med längden på sidorna i en rätvinklig triangel, och  är lika med längden på hypotenusan i en rätvinklig triangel.
är lika med längden på hypotenusan i en rätvinklig triangel. - Du använder Pythagoras sats eftersom diagonalen i en rektangel delar upp den i två kongruenta räta trianglar. Längden och bredden på rektangeln är längden på triangelns sidor; diagonalen är triangelns hypotenusa.

2. Tillämpa längden och bredden på formeln. Dessa är om det ges rätt, eller så kan du mäta dem. Se till att ersätta  och
och  .
.
 och
och  .
. .
.
3. Kvadra längden och bredden och lägg sedan ihop dessa siffror. Kvadring är att multiplicera talet med sig själv.




4. Subtrahera kvadratroten från varje sida av ekvationen. Det enklaste sättet att hitta en kvadratrot är att använda en miniräknare. Du kan använda en onlineräknare om du inte har en vetenskaplig miniräknare. Detta ger dig värdet  , eller triangelns hypotenusa och rektangelns diagonal.
, eller triangelns hypotenusa och rektangelns diagonal.
 , eller triangelns hypotenusa och rektangelns diagonal.
, eller triangelns hypotenusa och rektangelns diagonal.


Så diagonalen eller rektangeln med en bredd på 3 cm och en längd på 4 cm är 5 cm.
Metod 2 av 3: Använda arean och omkretsen

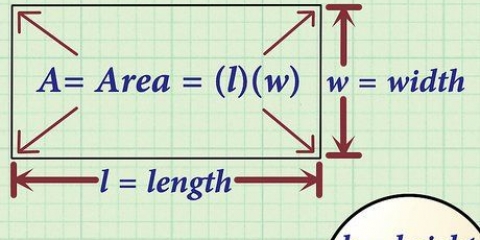
1. Skriv formeln för arean av en rektangel. Formeln är  , varigenom
, varigenom  är lika med arean av rektangeln,
är lika med arean av rektangeln,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd.
 , varigenom
, varigenom  är lika med arean av rektangeln,
är lika med arean av rektangeln,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd.
2. Använd arean av rektangeln i formeln. Se till att du byter ut rätt variabel  .
.
 .
. .
.
3. Ordna om formeln så får du ett värde för w  . Det gör du genom att dividera båda sidor av ekvationen med
. Det gör du genom att dividera båda sidor av ekvationen med  . Lägg detta värde åt sidan. Du kommer att använda detta senare i formeln för omkretsen.
. Lägg detta värde åt sidan. Du kommer att använda detta senare i formeln för omkretsen.
 . Det gör du genom att dividera båda sidor av ekvationen med
. Det gör du genom att dividera båda sidor av ekvationen med  . Lägg detta värde åt sidan. Du kommer att använda detta senare i formeln för omkretsen.
. Lägg detta värde åt sidan. Du kommer att använda detta senare i formeln för omkretsen.
 .
.
4. Skriv formeln för omkretsen av en rektangel. Formeln är  , varigenom
, varigenom  är lika med rektangelns bredd, och
är lika med rektangelns bredd, och  är lika med längden på rektangeln.
är lika med längden på rektangeln.
 , varigenom
, varigenom  är lika med rektangelns bredd, och
är lika med rektangelns bredd, och  är lika med längden på rektangeln.
är lika med längden på rektangeln.
5. Använd värdet på omkretsen i formeln. Se till att ersätta variabeln  .
.
 .
. .
.
6. Dividera båda sidor av ekvationen med 2. Detta ger dig värdet  .
.
 .
.

 .
.
7. Använd värdet w  i ekvationen. Använd värdet du hittade genom att ordna om areaformeln.
i ekvationen. Använd värdet du hittade genom att ordna om areaformeln.
 i ekvationen. Använd värdet du hittade genom att ordna om areaformeln.
i ekvationen. Använd värdet du hittade genom att ordna om areaformeln. , då byter du ut värdet
, då byter du ut värdet  i omkretsformeln:
i omkretsformeln:


8. Eliminera bråkdelen i ekvationen. Det gör du genom att multiplicera båda sidor av ekvationen med  .
.
 .
.



9. Sätt ekvationen lika med 0. Du gör detta genom att subtrahera förstagradstermen från båda sidor av ekvationen.




10. Ordna om ordningen på termerna i ekvationen. Det betyder att termen med exponenten kommer först, följt av termen med variabeln och slutligen konstanten. När du omarrangerar, var uppmärksam på de korrekta positiva och negativa tecknen. Ekvationen är nu ordnad som andragradsekvation.
 blir
blir  .
.
11. Faktorisera andragradsekvationen. För detaljerade instruktioner om hur du gör detta, läs artikeln Lös andragradsekvationer.
 kan lösas upp i
kan lösas upp i  .
.
12. Bestäm värdena för l  . Det gör du genom att nollställa varje term och lösa variabeln. Du får två lösningar på denna ekvation. Eftersom du har att göra med en rektangel kommer de två lösningarna att vara bredden och längden på din rektangel.
. Det gör du genom att nollställa varje term och lösa variabeln. Du får två lösningar på denna ekvation. Eftersom du har att göra med en rektangel kommer de två lösningarna att vara bredden och längden på din rektangel.
 . Det gör du genom att nollställa varje term och lösa variabeln. Du får två lösningar på denna ekvation. Eftersom du har att göra med en rektangel kommer de två lösningarna att vara bredden och längden på din rektangel.
. Det gör du genom att nollställa varje term och lösa variabeln. Du får två lösningar på denna ekvation. Eftersom du har att göra med en rektangel kommer de två lösningarna att vara bredden och längden på din rektangel.

OCH

 .
.Så längden och bredden på rektangeln är 7 cm och 5 cm.

13. Skriv formeln för Pythagoras sats. Formeln är  , varigenom
, varigenom  och
och  är lika med längden på sidorna i en rätvinklig triangel, och
är lika med längden på sidorna i en rätvinklig triangel, och  är lika med längden på hypotenusan i en rätvinklig triangel.
är lika med längden på hypotenusan i en rätvinklig triangel.
 , varigenom
, varigenom  och
och  är lika med längden på sidorna i en rätvinklig triangel, och
är lika med längden på sidorna i en rätvinklig triangel, och  är lika med längden på hypotenusan i en rätvinklig triangel.
är lika med längden på hypotenusan i en rätvinklig triangel.
14. Använd latitud och longitud i formeln. Det spelar ingen roll vilket värde du använder för vilken variabel.
 .
.
15. Kvadrera latitud och longitud och lägg sedan ihop dessa siffror. Att kvadrera betyder att multiplicera ett tal med sig själv.




16. Ta kvadratroten av varje sida av ekvationen. Det enklaste sättet att hitta en kvadratrot är att använda en miniräknare. Du kan använda en onlineräknare om du inte har en vetenskaplig miniräknare. Detta ger dig värdet  , och det är triangelns hypotenusa och rektangelns diagonal.
, och det är triangelns hypotenusa och rektangelns diagonal.
 , och det är triangelns hypotenusa och rektangelns diagonal.
, och det är triangelns hypotenusa och rektangelns diagonal.


Så diagonalen för en rektangel med en yta på 35 cm och en omkrets på 24 cm är cirka 8,6 cm.
Metod 3 av 3: Använd sidornas area och relationella längder

1. Skriv en formel som förklarar förhållandet mellan längderna på sidorna. Du kan ändra längden ( ) eller bredden (
) eller bredden ( ) isolera. Lägg den här formeln åt sidan för ett ögonblick. Du kommer snart att använda den i ytformeln.
) isolera. Lägg den här formeln åt sidan för ett ögonblick. Du kommer snart att använda den i ytformeln.
 ) eller bredden (
) eller bredden ( ) isolera. Lägg den här formeln åt sidan för ett ögonblick. Du kommer snart att använda den i ytformeln.
) isolera. Lägg den här formeln åt sidan för ett ögonblick. Du kommer snart att använda den i ytformeln. - Till exempel, om du vet att bredden på en rektangel är 2 cm mer än dess längd, kan du skriva en formel som
:
.

2. Skriv formeln för arean av en rektangel. Formeln är  , varigenom
, varigenom  är lika med arean av rektangeln,
är lika med arean av rektangeln,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd.
 , varigenom
, varigenom  är lika med arean av rektangeln,
är lika med arean av rektangeln,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd. , varigenom
, varigenom  är lika med rektangelns bredd, och
är lika med rektangelns bredd, och  är lika med längden på rektangeln.
är lika med längden på rektangeln.
3. Använd arean av rektangeln i formeln. Se till att ersätta variabeln  .
.
 .
. .
.
4. Använd relationsformeln för längden (eller bredden) i formeln. Eftersom du har att göra med en rektangel spelar det ingen roll om du arbetar med variabel  eller
eller  .
.
 eller
eller  .
. , då ersätter du denna relation
, då ersätter du denna relation  i områdesformeln:
i områdesformeln:


5. Gör det till en andragradsekvation. Detta gör du genom att använda den fördelande egenskapen och multiplicera termerna inom parentes tillsammans, varefter du sätter ekvationen lika med 0.




6. Faktorisera andragradsekvationen. För detaljerade instruktioner om hur du gör detta, läs artikeln Lös andragradsekvationer.
 kan lösas upp som
kan lösas upp som  .
.
7. Bestäm värdena för l  . Det gör du genom att göra varje term lika med noll och lösa för variabeln. Du hittar två lösningar på ekvationen.
. Det gör du genom att göra varje term lika med noll och lösa för variabeln. Du hittar två lösningar på ekvationen.
 . Det gör du genom att göra varje term lika med noll och lösa för variabeln. Du hittar två lösningar på ekvationen.
. Det gör du genom att göra varje term lika med noll och lösa för variabeln. Du hittar två lösningar på ekvationen.

OCH

 .
.I det här fallet finns det ett negativt svar. Eftersom längden på en rektangel inte kan vara negativ vet du att längden måste vara 5 cm.

8. Använd värdet på längden (eller bredden) i din relationsformel. Detta kommer att ge dig längden på den andra sidan av rektangeln.
 , sedan anger du 5 som längd i formeln:
, sedan anger du 5 som längd i formeln:



9. Skriv formeln för Pythagoras sats. Formeln är  , varigenom
, varigenom  och
och  är lika med längden på sidorna i en rätvinklig triangel, och
är lika med längden på sidorna i en rätvinklig triangel, och  är lika med längden på hypotenusan i en rätvinklig triangel.
är lika med längden på hypotenusan i en rätvinklig triangel.
 , varigenom
, varigenom  och
och  är lika med längden på sidorna i en rätvinklig triangel, och
är lika med längden på sidorna i en rätvinklig triangel, och  är lika med längden på hypotenusan i en rätvinklig triangel.
är lika med längden på hypotenusan i en rätvinklig triangel.
10. Använd latitud och longitud i formeln. Det spelar ingen roll vilket värde du använder för vilken variabel.
 .
.
11. Kvadrera latitud och longitud och lägg sedan ihop dessa siffror. Att kvadrera betyder att multiplicera ett tal med sig själv.




12. Subtrahera kvadratroten från varje sida av ekvationen. Det enklaste sättet att hitta en kvadratrot är att använda en miniräknare. Du kan använda en onlineräknare om du inte har en vetenskaplig miniräknare. Detta ger dig värdet  , eller triangelns hypotenusa och därmed rektangelns diagonal.
, eller triangelns hypotenusa och därmed rektangelns diagonal.
 , eller triangelns hypotenusa och därmed rektangelns diagonal.
, eller triangelns hypotenusa och därmed rektangelns diagonal.


Så diagonalen för en rektangel med en bredd som är 2 cm mer än dess längd och har en yta på 35 cm, är cirka 8,6 cm.
"Beräkna längden på diagonalen i en rektangel"
Оцените, пожалуйста статью