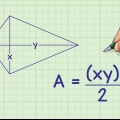
De två kortare sidorna av triangeln är kvadratens sidor: var och en har en längd s. Hypotenusan är kvadratens diagonal, d. 


Förenkla: 
Dela båda sidor med två: 
Area = 
Area = 

Anta till exempel att en kvadrat har en diagonal på 10 cm. Area = 
=
= 50 cm. Till exempel har en kvadrat med en diagonal på 10 cm längdsidor  centimeter.
centimeter. Om du vill hitta både längden på en sida och arean av diagonalen, kan du först använda denna formel och sedan kvadrera svaret för arean: Area  centimeter. Detta är något mindre korrekt, eftersom
centimeter. Detta är något mindre korrekt, eftersom  är ett irrationellt tal som kan ha avrundningsfel.
är ett irrationellt tal som kan ha avrundningsfel. Rita en fyrkant på papper. Se till att alla sidor är lika. Mät diagonalen. Rita en andra ruta med den längden som kvadratens sidor. Spåra en kopia av din första ruta så att du har två. Klipp ut alla tre rutor. Skär de två mindre rutorna i former som passar inuti den stora rutan. De måste fylla utrymmet perfekt för att visa att arean av den stora torget är exakt dubbelt så stor som arean av den mindre torget.
Beräkna arean av en kvadrat med hjälp av diagonalen
Den vanligaste formeln för arean av en kvadrat är enkel: det är längden på en av dess sidor i kvadrat, eller s. Men ibland vet man bara längden på en kvadrats diagonal, linjen mellan två motsatta hörn. Om du är bekant med räta trianglar kan du härleda en ny formel med diagonalen som enda variabel.
Steg
Del 1 av 2: Beräkna arean av en kvadrat

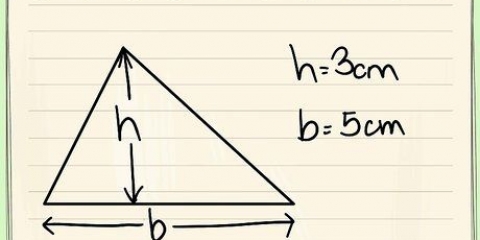
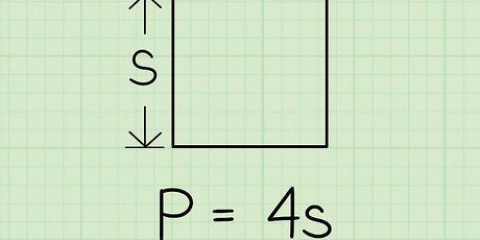
1. Rita din kvadrat. En kvadrat har fyra lika sidor. Låt oss säga att varje sida har längden "s".

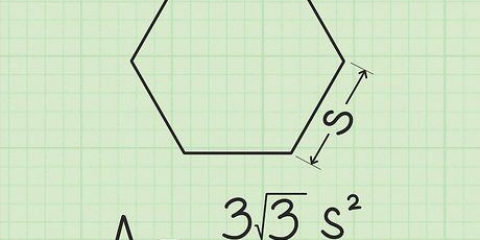
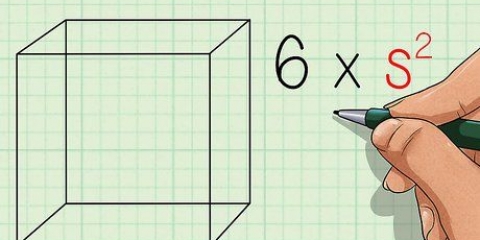
2. Använd standardformeln för arean av en kvadrat. Arean av en kvadrat är lika med dess längd gånger dess bredd. Eftersom varje sida s det blir formel Area = s x s = s. Detta kommer att visa sig vara användbart snart.

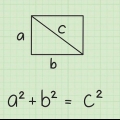
3. Anslut två motsatta hörn för att göra en diagonal. Måttet på denna diagonal blir d enheter. Denna diagonal delar kvadraten i två räta trianglar.

4.Använd Pythagoras sats för en av trianglarna. Pythagoras sats är en formel för att hitta hypotenusan (den längsta sidan) av en rätvinklig triangel: (sida A) + (sida B) = (hypotenusa) eller  . Nu när kvadraten har delats på mitten kan du använda den här formeln på en av de räta trianglarna:
. Nu när kvadraten har delats på mitten kan du använda den här formeln på en av de räta trianglarna:
 . Nu när kvadraten har delats på mitten kan du använda den här formeln på en av de räta trianglarna:
. Nu när kvadraten har delats på mitten kan du använda den här formeln på en av de räta trianglarna:

5. Ordna ekvationen så att s är på ena sidan. Kom ihåg att vi vet att arean på torget är s. Om du kan isolera s på ena sidan, har du en ny ekvation för området:






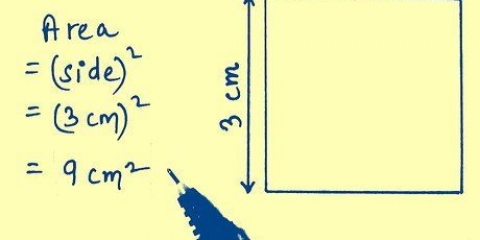
6. Använd denna formel med en exempelruta. Dessa steg har bevisat att formeln Area =  gäller alla rutor. Ange längden på diagonalen för d och lösa.
gäller alla rutor. Ange längden på diagonalen för d och lösa.
 gäller alla rutor. Ange längden på diagonalen för d och lösa.
gäller alla rutor. Ange längden på diagonalen för d och lösa.
=

= 50 cm.
Del 2 av 2: Ytterligare information
1. Hitta diagonalen för längden på en sida. Pythagoras sats för en kvadrat med sida s och diagonal d ge dig formeln  på. Lös för `d` om du känner till längderna på sidorna och vill bestämma längden på diagonalen:
på. Lös för `d` om du känner till längderna på sidorna och vill bestämma längden på diagonalen:
 på. Lös för `d` om du känner till längderna på sidorna och vill bestämma längden på diagonalen:
på. Lös för `d` om du känner till längderna på sidorna och vill bestämma längden på diagonalen: - Till exempel, om en kvadrat har sidor på 7 cm, är diagonalen d = 7√2 cm, eller cirka 9,9 cm.
- Om du inte har en miniräknare kan du använda 1,4 som en uppskattning av √2.
2. Bestäm längden på en sida med hjälp av diagonalen. Är diagonalen given och du vet att diagonalen för en kvadrat  sedan kan du dela båda sidor med
sedan kan du dela båda sidor med  till
till  att få.
att få.
 sedan kan du dela båda sidor med
sedan kan du dela båda sidor med  till
till  att få.
att få. centimeter.
centimeter. centimeter. Detta är något mindre korrekt, eftersom
centimeter. Detta är något mindre korrekt, eftersom  är ett irrationellt tal som kan ha avrundningsfel.
är ett irrationellt tal som kan ha avrundningsfel.3. Tolka ytformeln. Formeln Area =  verkar vara matematiskt korrekt, men finns det något sätt att testa detta direkt? Väl,
verkar vara matematiskt korrekt, men finns det något sätt att testa detta direkt? Väl,  är arean av en andra kvadrat med diagonalen som sida. Eftersom den fullständiga formeln
är arean av en andra kvadrat med diagonalen som sida. Eftersom den fullständiga formeln  du kan resonera att denna andra ruta har exakt dubbelt så stor yta som den ursprungliga torget. Du kan testa detta själv:
du kan resonera att denna andra ruta har exakt dubbelt så stor yta som den ursprungliga torget. Du kan testa detta själv:
 verkar vara matematiskt korrekt, men finns det något sätt att testa detta direkt? Väl,
verkar vara matematiskt korrekt, men finns det något sätt att testa detta direkt? Väl,  är arean av en andra kvadrat med diagonalen som sida. Eftersom den fullständiga formeln
är arean av en andra kvadrat med diagonalen som sida. Eftersom den fullständiga formeln  du kan resonera att denna andra ruta har exakt dubbelt så stor yta som den ursprungliga torget. Du kan testa detta själv:
du kan resonera att denna andra ruta har exakt dubbelt så stor yta som den ursprungliga torget. Du kan testa detta själv:Tips
- Denna enkla ekvation används inom många områden, inklusive kristallografi, kemi och konst. Till exempel kan du använda den för att beräkna arean av ett landskap du ser när du mäter, eller när du använder perspektiv i fotografi eller målning, genom att mäta avståndet du har gått och föreställa dig ett rutnät med det avståndet som diagonalen.
- Om du vill ta en mer visuell inställning till matematik, eller lära dig hur man använder grafer och diagram i konst, eller utforska spiralbanan för en partikel, kolla in några artiklar om Microsoft Excel, matematik, kalkylblad och grafik.
- Om du inte har en miniräknare men behöver en mer exakt uppskattning av kvadratroten ur två, finns det sätt att att göra detta för hand. Ett exempel på detta är Newton-Raphson-metoden.
"Beräkna arean av en kvadrat med hjälp av diagonalen"
Оцените, пожалуйста статью