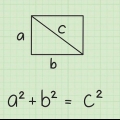
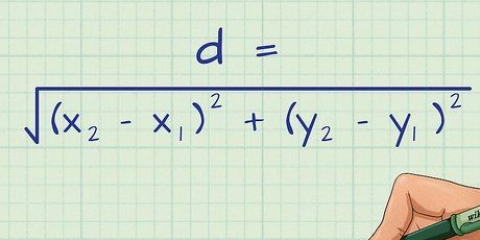Denna formel härrör från Pythagoras sats ( . En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna av kvadraten för att hitta längden på diagonalen (som är hypotenusan till den räta triangeln).
. En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna av kvadraten för att hitta längden på diagonalen (som är hypotenusan till den räta triangeln). 
Till exempel, om sidorna av kvadraten har en längd på 5 centimeter vardera, skulle formeln se ut så här:


Om du till exempel beräknar diagonalen för en kvadrat på 5 centimeter kommer din formel att se ut så här:


Så kvadratens diagonal är 7,07 centimeter lång. 

Till exempel, om kvadratens omkrets är 20 centimeter, skulle din formel se ut så här:


Till exempel:




Denna formel härrör från Pythagoras sats ( . En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna på kvadraten för att bestämma längden på diagonalen (hypotenusan i den räta triangeln).
. En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna på kvadraten för att bestämma längden på diagonalen (hypotenusan i den räta triangeln). 
Till exempel, om kvadraten har en längd på 5 centimeter, skulle formeln se ut så här:


Om du till exempel beräknar diagonalen för en kvadrat på 5 centimeter, skulle din formel se ut så här:


Så kvadratens diagonal är 7,07 centimeter lång. 

Till exempel, om arean av kvadraten är 25 kvadratcentimeter, skulle din formel se ut så här:


Till exempel:




Denna formel härrör från Pythagoras sats ( . En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på kvadratens sidor för att bestämma längden på diagonalen (hypotenusan i den räta triangeln).
. En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på kvadratens sidor för att bestämma längden på diagonalen (hypotenusan i den räta triangeln). 
Till exempel, om kvadraten har en längd på 5 centimeter, skulle formeln se ut så här:


Om du till exempel beräknar diagonalen för en kvadrat på 5 centimeter, skulle din formel se ut så här:


Så kvadratens diagonal är 7,07 centimeter.
Beräkna diagonalen för en kvadrat
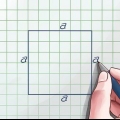
Diagonalen för en kvadrat är linjen från ett hörn av den kvadraten till det motsatta hörnet. För att hitta diagonalen för en kvadrat använder du formeln 

Steg
Metod 1 av 3: Om du vet längden på en sida

1. Hitta längden på en sida av kvadraten. Detta är förmodligen givet. Om du har att göra med en kvadrat i den verkliga världen, använd en linjal eller ett måttband för att bestämma dess längd. Eftersom alla fyra sidorna av kvadraten är lika långa kan du använda vilken sida som helst av kvadraten. Om du inte känner till kvadratens sidor kan du inte använda den här metoden.
- Hitta till exempel längden på diagonalen på en kvadrat med sidorna 5 centimeter.

2. Skriv ner formeln: . I formeln är
. I formeln är  lika med längden på diagonalen och
lika med längden på diagonalen och  lika med en sida av kvadraten.
lika med en sida av kvadraten.
 . I formeln är
. I formeln är  lika med längden på diagonalen och
lika med längden på diagonalen och  lika med en sida av kvadraten.
lika med en sida av kvadraten. . En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna av kvadraten för att hitta längden på diagonalen (som är hypotenusan till den räta triangeln).
. En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna av kvadraten för att hitta längden på diagonalen (som är hypotenusan till den räta triangeln).
3. Ange längden på sidan av kvadraten i formeln. Se till att ersätta variabeln  .
.
 .
.

4. Multiplicera längden på sidan med 2  . Detta ger längden på diagonalen. Denna beräkning görs bäst med en miniräknare, så att svaret blir mer exakt. Har ingen miniräknare, runda
. Detta ger längden på diagonalen. Denna beräkning görs bäst med en miniräknare, så att svaret blir mer exakt. Har ingen miniräknare, runda  sedan av till 1,414.
sedan av till 1,414.
 . Detta ger längden på diagonalen. Denna beräkning görs bäst med en miniräknare, så att svaret blir mer exakt. Har ingen miniräknare, runda
. Detta ger längden på diagonalen. Denna beräkning görs bäst med en miniräknare, så att svaret blir mer exakt. Har ingen miniräknare, runda  sedan av till 1,414.
sedan av till 1,414.

Så kvadratens diagonal är 7,07 centimeter lång.
Metod 2 av 3: När omkretsen är given

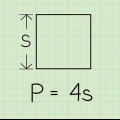
1. Skriv formeln för omkretsen av en kvadrat. Formeln är  , varigenom
, varigenom  är lika med kvadratens omkrets, och
är lika med kvadratens omkrets, och  lika med längden på en sida av kvadraten.
lika med längden på en sida av kvadraten.
 , varigenom
, varigenom  är lika med kvadratens omkrets, och
är lika med kvadratens omkrets, och  lika med längden på en sida av kvadraten.
lika med längden på en sida av kvadraten. - Denna metod fungerar bara om kvadratens omkrets anges.
- För att hitta längden på diagonalen måste du först hitta längden på en sida av kvadraten, så du måste använda formeln för omkretsen och
Att lösa.

2. Koppla in längden på omkretsen i formeln. Se till att du fyller i variabeln  .
.
 .
.

3. Lösa åt s  . För att göra detta, dividera varje sida av ekvationen med 4. Detta kommer att ge dig längden på en sida av kvadraten.
. För att göra detta, dividera varje sida av ekvationen med 4. Detta kommer att ge dig längden på en sida av kvadraten.
 . För att göra detta, dividera varje sida av ekvationen med 4. Detta kommer att ge dig längden på en sida av kvadraten.
. För att göra detta, dividera varje sida av ekvationen med 4. Detta kommer att ge dig längden på en sida av kvadraten.



4. Skriv formeln d = s 2  . I formeln är
. I formeln är  lika med längden på diagonalen och
lika med längden på diagonalen och  lika med en sida av kvadraten.
lika med en sida av kvadraten.
 . I formeln är
. I formeln är  lika med längden på diagonalen och
lika med längden på diagonalen och  lika med en sida av kvadraten.
lika med en sida av kvadraten. . En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna på kvadraten för att bestämma längden på diagonalen (hypotenusan i den räta triangeln).
. En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på sidorna på kvadraten för att bestämma längden på diagonalen (hypotenusan i den räta triangeln).
5. Koppla in längden på sidan av kvadraten i formeln. Se till att ersätta variabeln  .
.
 .
.

6. Multiplicera längden på sidan med 2  . Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt
. Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt  av vid 1,414.
av vid 1,414.
 . Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt
. Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt  av vid 1,414.
av vid 1,414.

Så kvadratens diagonal är 7,07 centimeter lång.
Metod 3 av 3: När arean anges

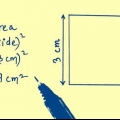
1. Skriv formeln för arean av en kvadrat. Formeln är  , varigenom
, varigenom  är lika med kvadratens yta, och
är lika med kvadratens yta, och  lika med längden på en sida av kvadraten.
lika med längden på en sida av kvadraten.
 , varigenom
, varigenom  är lika med kvadratens yta, och
är lika med kvadratens yta, och  lika med längden på en sida av kvadraten.
lika med längden på en sida av kvadraten. - Denna metod fungerar bara om torgets yta är känd.
- För att hitta längden på diagonalen måste du först bestämma längden på en sida av kvadraten, anledningen till att du först måste använda areaformeln, och
Att lösa.

2. Ersätt värdet för området i formeln. Se till att ersätta variabeln  .
.
 .
.

3. Lösa åt s  . Det gör du genom att bestämma kvadratroten av arean. Detta kommer att ge dig längden på en sida av kvadraten. Bestäm nu kvadratroten med en miniräknare. Om du behöver hjälp med att beräkna kvadratroten för hand, läs Beräkna kvadratroten ur ett tal utan miniräknare.
. Det gör du genom att bestämma kvadratroten av arean. Detta kommer att ge dig längden på en sida av kvadraten. Bestäm nu kvadratroten med en miniräknare. Om du behöver hjälp med att beräkna kvadratroten för hand, läs Beräkna kvadratroten ur ett tal utan miniräknare.
 . Det gör du genom att bestämma kvadratroten av arean. Detta kommer att ge dig längden på en sida av kvadraten. Bestäm nu kvadratroten med en miniräknare. Om du behöver hjälp med att beräkna kvadratroten för hand, läs Beräkna kvadratroten ur ett tal utan miniräknare.
. Det gör du genom att bestämma kvadratroten av arean. Detta kommer att ge dig längden på en sida av kvadraten. Bestäm nu kvadratroten med en miniräknare. Om du behöver hjälp med att beräkna kvadratroten för hand, läs Beräkna kvadratroten ur ett tal utan miniräknare.



4. Skriv formeln d = s 2  . I formeln är
. I formeln är  lika med längden på diagonalen och är
lika med längden på diagonalen och är  lika med en sida av kvadraten.
lika med en sida av kvadraten.
 . I formeln är
. I formeln är  lika med längden på diagonalen och är
lika med längden på diagonalen och är  lika med en sida av kvadraten.
lika med en sida av kvadraten. . En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på kvadratens sidor för att bestämma längden på diagonalen (hypotenusan i den räta triangeln).
. En diagonal delar en kvadrat i två kongruenta rätvinkliga trianglar, så du kan använda längden på kvadratens sidor för att bestämma längden på diagonalen (hypotenusan i den räta triangeln).
5. Använd längden på sidan av kvadraten i formeln. Se till att ersätta variabeln  .
.
 .
.

6. Multiplicera längden på sidan med 2  . Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt
. Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt  av vid 1,414.
av vid 1,414.
 . Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt
. Detta kommer att ge dig längden på diagonalen. Det är bäst att göra denna beräkning med en miniräknare för att få ett mer exakt resultat. Om du inte har en miniräknare, avrunda uppåt  av vid 1,414.
av vid 1,414.

Så kvadratens diagonal är 7,07 centimeter.
Förnödenheter
- Kalkylator
"Beräkna diagonalen för en kvadrat"
Оцените, пожалуйста статью