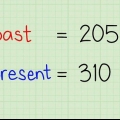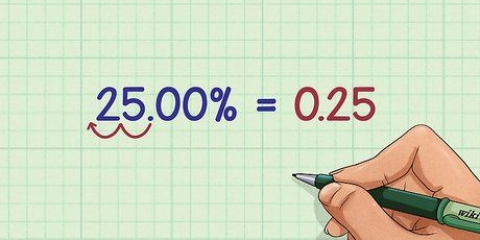Beräkna procentuell förändring: 7 steg (med bilder)

Steg
- Del 1 av 2: Beräkna procentuell förändring i allmänna fall
- Del 2 av 2: Specialfall
Tips
Tips 2

I matematik används en procentuell förändring för att ange sambandet mellan ett gammalt värde/belopp och ett nytt värde/belopp. Procentuell förändring uttrycker denna skillnad i procent av det gamla värdet.I de flesta fall där V₁ representerar det gamla, initiala värdet och V₂ det nya eller nuvarande värdet, den procentuella förändringen kan hittas med formeln ((V₂-V₁)/V₁) × 100. Observera att denna enhet uttrycks som en procentsats. Se steg 1 nedan för en förklaring av denna procedur.

Steg

Del 1 av 2: Beräkna procentuell förändring i allmänna fall

1. Hitta gamla och nya värden för en viss variabel. Som nämnts i inledningen är syftet med de flesta procentuella förändringsberäkningar att fastställa förändra av en variabel kontra tid. För detta behöver du två olika värden – en gammal (eller "komma igång") värde och ett nytt (eller "slutet") där den. Ekvationen för procentuell förändring ger procentuell förändring av dessa två punkter.

Ett exempel på detta finns i detaljhandelns värld. När en viss produkt sänks i pris uttrycks det ofta som "X% rabatt" – med andra ord, eftersom den procentuella förändringen från det gamla priset. Anta att en viss typ av byxor brukade kosta €50 och nu säljs för €30. I detta exempel 50 € de "gammal" värde, och 30 € är vår"nya" där den. I nästa steg kommer vi att beräkna den procentuella förändringen mellan dessa två priser.

Bild med titeln Balance a Checkbook Steg 6

2. Subtrahera det gamla värdet från det nya. Det första steget för att bestämma den procentuella förändringen mellan två värden är att hitta skillnad. Skillnaden mellan två tal hittas genom att subtrahera de två värdena. Anledningen till att vi subtraherar det gamla värdet från det nya (och inte tvärtom) är för att det bekvämt ger oss en negativ procentsats som det slutliga svaret om värdet minskar och ett positivt värde om detta värde ökar.

I exemplet börjar vi med $30, det nya värdet, och subtraherar $50 från det. 30 - 50 = -20 €.

Bild med titeln Ansök om ett entreprenörsbidrag Steg 14

3. Dela ditt svar med startvärdet. Ta nu svaret du fick och dividera det med startvärdet. Detta ger det proportionella förhållandet mellan värdeförändringen från det gamla initiala värdet, uttryckt som decimal. Med andra ord, detta representerar den totala förändringen i din variabels värde från dess initiala värde.

I vårt exempel kommer att dividera skillnaden (av start- och slutvärdena; -$20) med startvärdet ($50) sluta med -20/50 = -0,40 lämna tillbaka. Ett annat sätt att tänka på detta är att värdeförändringen på 20 USD är 0,40 av 50 USD (startvärdet), och värdeförändringen var i negativ riktning.

Bild med titeln Beräkna mängden matfrimärken Steg 2

4. Multiplicera ditt svar med 100 för procentsatsen. Den procentuella förändringen uttrycks (logiskt) i procent och inte i decimaler. För att konvertera ditt decimalsvar till en procent, multiplicera det med 100. Efter det behöver du bara lägga till ett procenttecken. Grattis! Detta värde indikerar den procentuella förändringen från det gamla till det nya värdet.

För att få det slutgiltiga svaret i vårt exempel multiplicerar vi svaret (-0,40) med 100. -0,40 × 100 = -40 %. Detta svar betyder att det nya priset på 30 € för byxorna är 40 % är lägre än det gamla priset på €50. Byxorna är med andra ord 40% billigare. Ett annat sätt att tänka på detta är att skillnaden på 20 USD i pris är 40 % mindre än det ursprungliga priset på 50 USD – eftersom detta resulterar i en lägre slutpriset får det ett negativt tecken.

Observera att ett positivt svar som en slutlig procentsats innebär en ökning av värdet på din variabel. Till exempel, om det slutliga svaret på exempelproblemet inte var -40 % utan 40 %, skulle det betyda att byxans nypris var 70 USD; 40 % Sjö än det ursprungliga priset på 50 €.

Del 2 av 2: Specialfall

Bild med titeln Skaffa ett patent Steg 6

1. När du har att göra med variabler där värdet ändras flera gånger, bestäm bara den procentuella förändringen för de två värden du vill jämföra. Att bestämma procentuell förändring för en given variabel som ändrar värde flera gånger än en gång kan verka lite knepigt, men antalet gånger ett värde ändras gör inte saker och ting mer komplicerade än de är. Ekvationen för en procentuell förändring jämför inte mer än två värden samtidigt. Detta innebär att om du blir ombedd att beräkna den procentuella förändringen i en situation där en variabel med flera värdeförändringar är involverad, beräkna endast den procentuella förändringen mellan de 2 angivna värdena. Beräkna inte de procentuella förändringarna mellan varje värde i serien, varefter man räknar ut ett medelvärde eller summa av dem. Detta är inte detsamma som den procentuella förändringen mellan två poäng och kan lätt ge orimliga svar.

Anta till exempel att ett par byxor har ett startpris på 50 USD. Efter en rabatt blir detta €30 och efter en prisändring €40. I slutändan, efter en sista rabatt, kommer priset till 20 €. Ekvationen för procentuell förändring kan ge procentuell förändring mellan två av dessa värden; de andra två värdena är inte nödvändiga. För att till exempel hitta den procentuella förändringen mellan startpriset och slutpriset, ta $50 och $20 som "gammal" och "nya" värden.Lös detta på följande sätt:

((V₂-V₁)/V₁) × 100
((20 - 50)/50) × 100
(-30/50) × 100
-0,60 × 100 = -60 %

Bild med titeln Gör dina egna skatter Steg 23

2. Dividera det nya värdet med det gamla värdet och multiplicera med 100 för att hitta det absoluta förhållandet mellan båda värdena. En process som liknar (men inte identisk) med den process som används för att bestämma den procentuella förändringen används för att bestämma det absoluta procentuella förhållandet mellan "gammal" och "nya" värden. För att göra detta, dividera helt enkelt det gamla värdet med det nya värdet och multiplicera det med 100 - detta ger dig en procentsats som direkt jämför det nya värdet med det gamla, snarare än att uttrycka förändringen mellan de två.

Observera att genom att subtrahera %100 från detta svar får du den procentuella förändringen igen.

Låt oss använda denna process tillsammans med exemplet med rabatterade byxor. Om byxorna har ett startpris på €50 och slutar på €20, då 20/50 × 100 = 40 %. Detta säger oss att $20 är lika med 40% av $50. Observera att genom att subtrahera 100 % får vi den procentuella förändringen beräknad ovan: 40 - 100 = -60 %.

Denna process kan ge svar över 100 %. Till exempel, om 50 € är det gamla priset och €75 det nya priset, då gäller följande: 75/50 ×100 = 150 %. Det betyder att 75€ är lika med 150% av 50€.

Bild med titeln Köp en aktie utan en aktiemäklare Steg 2

3. I allmänhet använder du absolut förändring när du har att göra med 2 procent. Terminologin som används för att beräkna procentuell förändring kan ibland vara lite förvirrande när de två värdena som jämförs själva är procentsatser. I de fallen är det viktigt att skilja på procentuell förändring och absolut förändring. Det senare är det exakta antalet procentenheter där det nya värdet skiljer sig från det gamla värdet - inte det nu bekanta begreppet procentuell förändring som vi har behandlat det.

Anta till exempel att ett par skor erbjuds med 30 % rabatt (en -30 % procentuell förändring från det gamla priset). Om rabatten höjs till 40% (en procentuell förändring på -40% från det gamla priset), så är det inte felaktigt att säga att den procentuella förändringen av denna rabatt är lika med ((-40 - -30) /-30 ) × 100 = 33,33 %. Med andra ord, Byxorna har en rabatt som är 33,33% "högre" än den tidigare rabatten.

Men, detta anges vanligtvis som en"10% högre rabatt". Med andra ord hänvisar vi vanligtvis till absolut förändring två procentenheter än den procentuella förändringen.

Tips

Om det ordinarie priset för en vara är 50,00 USD och du köpte den på rea för 30,00 USD, är den procentuella förändringen:

(50,00 € - 30,00 €)/50,00 € × 100 = 20/50 × 100 = 40 %

Priset du köpte den till var lägre än det ursprungliga priset, så detta är en minskning med 40 procent. Du har alltså sparat 40% på utgångspriset.

Anta nu att du vill sälja de köpta byxorna igen. Till exempel, om du köpte byxorna för 30 USD och senare säljer dem för 50 USD, är förändringen 50 USD - 30 USD = 20 USD. Det ursprungliga värdet var $30, så den procentuella förändringen är:

(50,00 € - 30,00 €)/30,00 € × 100 = 20/30 × 100 = 66,7 %

Så värdet på byxorna ökade med 66,7% av det ursprungliga priset. En prisökning på 66,7 %.

När värdet på byxorna sjönk från €50 till €30 var värdeminskningen 40 %. När byxorna ökade i pris från €30 tillbaka till €50, var värdeökningen 66,7 %. Men det är viktigt att notera att det vinstfrekvens till ett pris av 50 € var fortfarande inte mer än 40 %, eftersom det är baserat på ökningen med 20 €. Detta står i motsats till värderingsvärdet.