Denna process är i princip samma sak som att först beräkna arean av basen och sedan multiplicera denna area med kubens höjd (eller med andra ord längd × bredd × höjd), eftersom arean av basen bestäms genom att multiplicera längden med bredden. Eftersom längden, bredden och höjden på en kub är lika, kan vi förenkla processen genom att höja ett av dessa värden till tredje potens. Låt oss fortsätta med vårt exempel. Längden på kanten var 2 cm, så volymen på kuben är 2 x 2 x 2 (eller 2)= 8. 
I vårt exempel angavs längden på revbenet i centimeter, så svaret måste anges i kubikcentimeter. Så svaret är 8 cm. 

Så i vårt exempel dividerar vi femtio med sex: 50/6 = 8,33 cm. Kom ihåg att enheterna för tvådimensionella svar skrivs i kvadrat (cm, m och så vidare). 
I vårt exempel är √8,33 = 2,89 cm. 
Så i vårt exempel: 2,89 × 2,89 × 2,89 = 24,14 cm. Glöm inte att skriva svaret i kubikenheter. 

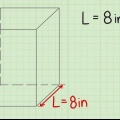
Detta kan också härledas från Pythagoras sats. d, d och l bilda en liksidig triangel med D som hypotenusa, alltså d = d + l. Tidigare hade vi redan bestämt: d = 2l, så vi kan också säga följande: d = 2l + l = 3l. Antag att vi vet att längden på diagonalen som går från ett hörn i kubens bas till det motsatta hörnet i kubens övre yta är 10 meter. Så om vi vill beräkna volymen anger vi 10 i formeln ovan för d. d = 3l. 10 = 3l. 100 = 3l 33.33 = l 5.77 m = l. Från denna punkt kan vi beräkna volymen genom att höja längden på revbenet till kuben. 5.77 = 192.45 m
Beräkna volymen av en kub
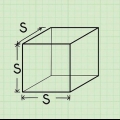
En kub är en tredimensionell figur vars längd, bredd och höjd är lika. En kub har sex kvadratiska ytor, vars sidor är lika långa och vinkelräta mot varandra. Att beräkna volymen på en kub är väldigt enkelt - vanligtvis behöver du bara multiplicera följande: längd × bredd × höjd. Eftersom kanterna på en kub alla har samma längd kan du också se volymen på en kub enligt följande: l, varigenom l är längden på en av kubens kanter. Gå till steg 1 för en detaljerad förklaring.
Steg
Metod 1 av 3: Höj kanten på kuben till kuben

1. Hitta längden på en av kubens kanter. Ofta kommer du att se en summa där längden på ett av revbenen redan är angiven. När du har den här informationen har du allt du behöver för att bestämma kubens volym. Använd en linjal eller ett måttband om du inte löser ett matematiskt problem, utan bara vill veta volymen på ett befintligt kubformat objekt.
- För att bättre förstå processen för att bestämma volymen av en kub, låt oss börja med en exempelsumma när vi går igenom stegen i det här avsnittet. Antag att kanten på kuben 2 cm lång är. Vi kommer att använda denna information i nästa steg för att bestämma volymen på kuben.

2. Höj längden på revbenet till tredje potens. När du har längden på ett av revbenen, höj sedan denna siffra till tredje potens. Med andra ord, multiplicera talet två gånger med sig själv. om l är längden på revbenet, då multiplicerar du l × l × l (eller i enklare form l). Resultatet är kubens volym.

3. Ange ditt svar i kubikenheter. Volym är måttet på ett tredimensionellt utrymme, så lösningen måste skrivas i kubikenheter. På ett test kan det kosta dig poäng om du inte anger svaret korrekt i kubikenheter, så glöm inte!
Metod 2 av 3: Bestämning av volym efter yta

1. Hitta området för ansiktena på din kub. De lättast sättet att bestämma volymen är genom att höja revbenet till kuben, men det är inte några sätt. Längden på kanten av en kub eller arean av en av dess ytor kan härledas från flera andra egenskaper hos kuben, vilket innebär att om du börjar med denna information kan du bestämma kubens volym på ett derivativt sätt. Till exempel, om du bara känner till den totala arean av alla sidor av kuben, kan du hitta volymen genom att dividera denna area med sex och sedan ta kvadratroten av det numret för att hitta längden på kanten. Från den punkten kan du höja till tredje potens igen. I det här avsnittet går vi igenom processen steg för steg.
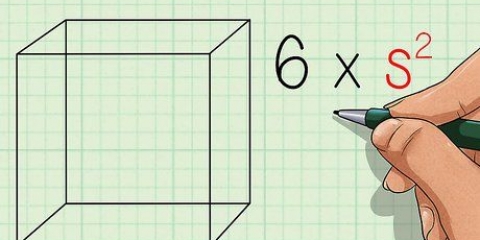
- Arean av en kub ges av formeln 6l, varigenom l är längden på en av kubens kanter. Denna formel är faktiskt samma sak som att bestämma den tvådimensionella arean av en av kubens sidor och sedan lägga till de sex (lika) områdena. Vi kommer att använda den här formeln för att bestämma kubens volym från kubens område.
- Anta att vi har en kub som vi vet att området 50 cm är, men vi vet inte vad längden på revbenen är. I nästa steg kommer vi att använda denna information för att hitta volymen på kuben.

2. Dela arean av kuben med sex. Eftersom kuben har sex ytor med lika stor yta, kan vi bestämma arean på ett ansikte genom att dividera kubens yta med sex. Arean av ett plan är densamma som multiplikationen av två kanter (l × b, b × h eller h × l).

3. Hitta kvadratroten av detta värde. Eftersom arean av en av ytorna på en kub är lika med l (l × l), kan vi nu ta kvadratroten av det hittade värdet för att bestämma längden på ett av revbenen. När du väl vet detta har du tillräckligt med information för att beräkna volymen på kuben som vanligt.

4. Höj denna siffra till tredje potens för att hitta kubens volym. Nu när du har bestämt ett värde för längden på revbenen kan du höja detta nummer till kuben för att bestämma volymen enligt beskrivningen i det första avsnittet i denna artikel.
Metod 3 av 3: Bestämma volymen med hjälp av diagonaler

1. Dela diagonalen på en av kubens ytor med √2 för att hitta längden på kubens kanter. Diagonalen för en kvadrat är √2 × längden på en av dess kanter. Med andra ord, om du bara vet värdet på en av diagonalerna på en yta på kuben, kan du beräkna längden på kubens kanter genom att dividera detta värde med √2. Från den punkten kan du höja till tredje potens igen och bestämma volymen enligt beskrivningen ovan.
- Antag att en av kubens ytor har en diagonal på7 meter lång. Sedan kan vi beräkna längden på ett av revbenen genom att dividera 7 med √2. 7/√2 = 4,96 meter. Nu när vi vet längden på kubens kanter kan vi beräkna kubens volym genom att höja 4,96 till kuben: 4,96 = 122,36 meter.
- Var uppmärksam: d = 2l, Sann d är längden på diagonalen på en av kubens ytor och l är längden på en av kubens kanter. Detta kan härledas från Pythagoras sats, där kvadraten på hypotenusan i en liksidig triangel är lika med summan av kvadraten på de andra två sidorna. Eftersom diagonalen på en yta av en kub bildar en liksidig triangel med två av kanterna på den ytan, kan vi säga följande: d = l + l = 2l.

2. Hitta kvadraten på diagonalen mellan två motsatta hörn av kuben, dividera med tre och ta kvadratroten för att hitta längden på en av kanterna. Om längden på den tredimensionella linjen mellan två motsatta hörn av kuben är den enda givna, kan du fortfarande bestämma kubens volym. d bildar en av sidorna i en liksidig triangel vars hypotenusa är linjen mellan två motsatta hörn av kuben, så vi kan säga: d = 3l, där D är den tredimensionella linjen mellan två motsatta hörn av kuben.
"Beräkna volymen av en kub"
Оцените, пожалуйста статью