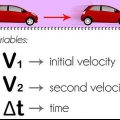
Avståndet ska visas i meter (SI-enhet). I vårt exempel på tåget bestämmer vi det arbete som utförs på tåget när det rör sig längs spåret. Om startpunkten är satt till 0 och slutpunkten till 2 meter, så säger vi att förskjutningen D är lika med 2 meter. 
Observera att kraftenheten är Newton. Anta att vi inte vet storleken på kraften i detta exempel. Men vi vet att tågets massa är lika med 0,5 kg och att kraften får det att accelerera med 0,7 m/s. I det här fallet kan vi hitta storleken med M x A = 0,5 x 0,7 = 0,35 Newton. 
Nu är det dags att fixa det faktiska problemet. Med ett värde för kraften på 0,35 Newton och ett värde för förskjutningen på 2 meter blir svaret: 0,35 × 2 = 0,7 joule. Du kanske har märkt att det i formeln som anges i introt finns ytterligare en del: cos(θ). Som nämnts ovan är rörelsens kraft och riktning densamma. Det betyder att vinkeln mellan dem är lika med 0. Eftersom cos(0) = 1 behöver vi inte vinkeln, eftersom den är lika med 1. 
Observera att det finns ett alternativt uttryck för joule; 1 watt per sekund. Se nedan för en närmare behandling av makt i förhållande till arbete. 

I vårt exempelproblem säger vi att kraften appliceras från en vinkel på 60 grader från horisontalplanet. Om tåget fortfarande rör sig horisontellt är vinkeln mellan tågets förskjutning och kraften lika med 60. 
Låt oss nu lösa provproblemet. Med hjälp av en miniräknare bestämmer vi att cos 60 är lika med 1/2. Fyll i detta i formeln så kan vi lösa: 10 Newton × 2 meter × 1/2 = 10 joule. 

Anta att det, baserat på ovanstående exempel, tog 12 sekunder att flytta tåget 5 meter. I så fall delar vi det utförda arbetet (86,6 joule) med tiden (12 sekunder) för att hitta svaret. Så kraften är: 86.6/12 = `7,22 watt. 
Till exempel, i exempelproblemet två steg tidigare, kan vi anta att tåget i princip hade en total mekanisk energi på 100 joule. Eftersom kraften drar tåget i detta exempel, i rörelseriktningen, är den positiv. Tågets energi är TMEi + Wnc = 100 + 86,6 = 186, joule. Observera att icke-konservativa krafter är de krafter där kraften som krävs för att accelerera ett objekt beror på objektets väg. Friktion är ett bra exempel; ett föremål som skjuts en kort rak bana till en viss punkt kommer att uppleva mindre friktion i genomsnitt än ett objekt som skjuts en längre slingrande bana till samma ändpunkt som den korta banan.
Beräkna arbetskraft
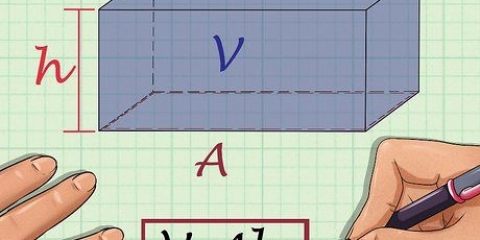
I fysik betyder "arbetskraft" något helt annat än dagligt tal. För att vara exakt, termen "arbetskraft" används när en fysisk kraft får ett föremål att röra sig. I allmänhet gäller att ju större förskjutning en given kraft har, desto mer arbete utförs. Arbete kan beräknas med formeln Arbete = F × D × cos(θ), där F = kraft (i newton), D = förskjutning (i meter) och θ = vinkeln mellan vektorkraften och rörelseriktningen.
Steg
Del 1 av 3: Att bestämma arbete i en dimension

1. Bestäm kraftens riktning och rörelsens riktning. Till att börja med är det viktigt att bestämma både kraftens riktning och föremålets riktning. Kom ihåg att föremål inte alltid rör sig i samma riktning som kraften som appliceras på dem; till exempel, om du drar en liten vagn i handtaget, applicerar du en diagonal kraft på den (om du är längre än vagnen är hög) för att flytta den framåt. I detta avsnitt behandlar vi situationer där kraft och rörelse "väl" går åt samma håll. För information om hur man beräknar arbetskraft så här "inte" i så fall kan du läsa mer nedan.
- För att klargöra detta kommer vi att lösa följande problem. Anta att ett leksakståg dras av ett lok. I detta fall är både kraftvektorn och tågets rörelseriktning lika med varandra; fram-. I de kommande stegen använder vi denna information för att beräkna det arbete som utförs av loket.

2. Bestäm objektets förskjutning. Den första variabeln vi behöver för arbetsformeln är D, eller förskjutning, som vanligtvis är lätt att hitta. Förskjutning är avståndet som ett föremål flyttas, i en rak linje. I vetenskapliga problem ges vanligtvis denna information, eller så är det möjligt att sluta sig till det från data. I den verkliga världen kan du hitta förskjutningen genom att mäta avståndet mellan start- och slutpunkten (inte längs vägen, men "fågelvägen").

3. Bestäm kraften som utövas på föremålet. Bestäm sedan storleken på kraften som används för att få föremålet att röra sig. Detta är ett mått för "storlek" av kraften; ju större kraften är, desto större blir accelerationen av föremålet. Om storleken på kraften inte är given kan du härleda den från föremålets massa och acceleration (förutsatt att det inte finns några andra krafter att ta hänsyn till) enligt formeln F = M xA.

4. Multiplicera kraften gånger avståndet. Om du vet storleken på kraften på föremålet och avståndet det har förflyttat sig, är resten lätt. Multiplicera dessa två värden tillsammans för att hitta verket.

5. Ge svaret i joule. I fysik, o.a. arbetskraft nästan alltid uttryckt i joule. 1 Joule definieras som 1 Newton utövad på 1 meter, eller med andra ord, 1 Newton × meter. Detta verkar logiskt eftersom man multiplicerar ett avstånd med kraft och alltså uttrycker detta i Nm.
Del 2 av 3: Hitta arbete när kraft appliceras från en vinkel

1. Bestäm kraften och förskjutningen som vanligt. Ovan diskuterade vi ett problem om arbete, där föremålet och kraften går åt samma håll. I verkligheten är det ofta inte så. I de fall där kraften på och objektets rörelse är motsatta, måste du ta hänsyn till skillnaden mellan de två, och inkludera detta i beräkningen för rätt resultat. För att börja, hitta storleken på kraften och förskjutningen av föremålet som vanligt.
- Låt oss titta på ett annat exempel. I det här fallet, låt oss säga att vi drar tåget precis som i föregående exempel, men draget är vinklat uppåt. Vi kommer att ta hänsyn till detta i nästa steg, men för nu håller vi oss till grunderna: tågets förskjutning och storleken på kraften på tåget. Antag att kraften har en storlek på 10 newton och att förskjutningen återigen är lika med 2 meter, som förut.

2. Bestäm nu vinkeln mellan kraftens riktning och förskjutningen. Till skillnad från exemplen som beskrivits ovan är det nu nödvändigt att bestämma skillnaden mellan de två riktningarna, uttryckt i vinkeln. Om dessa data inte ges kan du mäta detta eller härleda detta från annan information som du har.

3. Multiplicera kraften F gånger förskjutningen D gånger vinkeln cos(θ). När du väl känner till förskjutningen, kraften och vinkeln (mellan vektor och rörelse) är lösningen nästan lika enkel som den är utan att ta hänsyn till vinkeln. Ta bara cos för vinkeln (du behöver förmodligen en miniräknare för detta) och multiplicera det med kraften och förskjutningen för att hitta ditt svar (i joule).
Del 3 av 3: Använd ett värde för arbete

1. Du kan också invertera formeln för att hitta avståndet, kraften eller vinkeln. Formeln ovan är naturligtvis användbar inte bara för att hitta arbete utan också, om det ges arbete, för att hitta de andra variablerna i samma formel. I dessa fall isolerar du bara den variabel du vill beräkna och lösa enligt enkla algebraiska principer.
- Antag att du vet att tåget dras med en kraft på 20 Newton i en vinkel och rör sig längs spåret en sträcka av 5 meter och gör 86,6 joule arbete. Men vi vet inte i vilken vinkel kraften verkar på föremålet. För att lösa detta, låt oss lägga variabeln separat och räkna ut det så här:
- 86,6 = 20 × 5 × cos(θ)
- 86,6/100 = cos(θ)
- arccos(0,866) = θ = 30

2. Dela med tiden det tog flytten för att hitta förmågan. Arbetskraft är direkt relaterad till "kraft". Makt är helt enkelt ett sätt att uttrycka mängden arbete som gjorts inom ett givet system under den tid det har tagit. Allt du behöver göra för att hitta kraften är det arbete som gjorts för att flytta objektet, dividera med tiden för flytten. Effekt uttrycks i enheter av watt (motsvarande Joule per sekund).

3. Använd formeln TMEi + Wnc = TMEf att hitta den mekaniska energin i ett system. Arbete kan också användas för att bestämma energin i ett givet system. I ovanstående formel, TMEi = är första total mekanisk energi i systemet, TMEf = den slutlig total mekanisk energi i systemet och Wnc = det arbete som gjorts på systemet på grund av icke-konservativa krafter.. I denna formel, om kraften rör sig med förskjutningsriktningen, är den positiv, och om den motsätter sig, är den negativ. Observera att båda variablerna för energi kan hittas med formeln (½)mv där m = massa och v = volym.
Tips
- Om du lyckas lösa ett problem, le och klappa dig själv på axeln!
- Träna ut så många övningar som möjligt, med vilka du lär dig förstå ämnet.
- Fortsätt öva och försök igen om det inte fungerar första gången.
- Lär dig följande punkter om arbete:
- Arbetet kan vara positivt eller negativt. (Här menar vi den fysiska betydelsen av positivt och negativt, inte den bokstavliga betydelsen.)
- Arbetet är negativt om kraften är motsatt förskjutningsriktningen.
- Arbete är positivt om kraften är lika med förskjutningsriktningen.
"Beräkna arbetskraft"
Оцените, пожалуйста статью