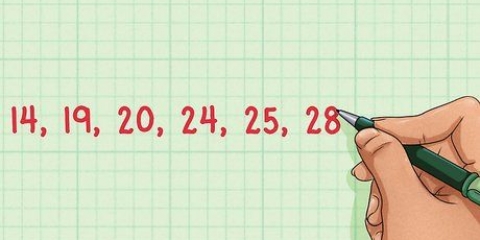Hur man beräknar lotteriodds

Steg
Tips
Varningar

Alla har hört jämförelser om oddsen att vinna på lotteriet kontra oddsen för andra osannolika händelser, som att bli träffad av blixten. Det är sant, oddsen för att vinna jackpotten på ett spel som Powerball eller något annat pick-6-lotteri är otroligt låga. Men hur lågt? Och hur ofta måste du spela för att öka din chans? Dessa svar kan hittas exakt med några enkla beräkningar.

Steg

Metod 1 av 3: Beräkna jackpottodds

1. Förstå de beräkningar som används. Oddsen för att vinna ett lotteri där nummer väljs från en sekvens, oavsett ordning, definieras av formeln

n! r! (n - r)!

${frac{n!}{r!(n-r)!}}$ . I den här formeln representerar n det totala antalet möjliga siffror och r representerar antalet siffror som kommer att väljas. den `!` står för factorial, där för varje heltal n är n*(n-1)*(n-2)... etc., tills 0 nås. Till exempel: 3! betyder då

3 \times 2 \times 1

$3 gånger 2 gånger 1$ .

Ett enkelt exempel: föreställ dig att du måste välja mellan två siffror och siffrorna 1 till 5. Din sannolikhet att välja de två "rätta" siffrorna (de vinnande numren) skulle då definieras som $5! 2! \times 3!$ ${frac{5!}{2!times 3!}}$ .
Detta löses sedan som $5 \times 4 \times 3 \times 2 \times 1 2 \times 1 \times 3 \times 2 \times 1$ ${frac{5gånger 4 gånger 3 gånger 2 gånger 1}{2 gånger 1 gånger 3 gånger 2 gånger 1}}$ , antingen $120 \div 12$ $120div 12$ , och det är 10.
Så din chans att vinna detta spel är 1 på 10.
Att beräkna faktorvärdet kan bli förvirrande, särskilt när det kommer till större siffror. De flesta miniräknare har en faktoriell funktion för att göra dessa beräkningar lite enklare. Alternativt kan du också gå in på fakulteten i Duck Duck Gos sökmotorer (som t.ex. `55!`) eller Google, för att få svaret.

Bild med titeln Beräkna Lotto-odds Steg 2

2. Bestäm lotterireglerna. Majoriteten av miljoner pengar, Powerball och andra stora lotterier, använder ungefär samma regler. Fem eller sex nummer väljs från en stor pool av nummer, i slumpmässig ordning. Siffror kan inte upprepas. I vissa spel läggs ett fast nummer till i slutet (Powerball i Powerball-spelen är ett exempel). Powerballs standardregler visar att fem nummer (exklusive Powerball) väljs bland 69 möjliga nummer.

Andra spel kan kräva att du väljer mellan fem eller sex nummer, eller fler, från en större eller mindre pool av nummer.

Bild med titeln Beräkna Lotto-odds Steg 3

3. Tillämpa siffrorna på ekvationen för sannolikheten. Den första delen av Powerball-sannolikheten beräknas som sannolikheten för att korrekt välja de första fem siffrorna. Detta beräknas bekvämt med den tidigare införda sannolikhetsformeln. Så ekvationen för dessa specifika linjer blir:

69! 5! (69 - 5)!

${frac{69!}{5!(69-5)!}}$ , att förenkla till

69! 5! \times 64!

${frac{69!}{5!times 64!}}$ .

Bild med titeln Beräkna lottoodds Steg 4

4. Beräkna din chans att välja rätt nummer. Att lösa ekvationen görs bäst med en sökmotor eller kalkylator, eftersom siffrorna som används är besvärliga att skriva ner mellan stegen. När den är löst blir ekvationen talet 11.238.ge 513. Det betyder att du har en chans på 1 på 11.238.513 för att välja de fem siffrorna korrekt.

Bild med titeln Beräkna Lotto-odds Steg 5

5. Multiplicera för att få det slutliga talet. För att ta hänsyn till sannolikheten att korrekt välja Powerball och vinna jackpotten behöver du helt enkelt multiplicera siffran från föregående resultat med storleken på Powerball-poolen. För standardspelet finns det 26 möjliga Powerball-nummer. Så du multiplicerar det föregående resultatet (11.238.513 i det här fallet) med det slutliga talet (som är 26), för att beräkna din slutliga sannolikhet (som är 292.201.338).

Så din chans att korrekt välja de första fem siffrorna och Powerball är 1 på 292.201.338.

Metod 2 av 3: Bestämma sannolikheten för mindre priser

Bild med titeln Beräkna Lotto-odds Steg 6

1. Börja med jackpottchansen. I de flesta fall finns det mindre priser tillgängliga som kräver att du väljer några av siffrorna korrekt. Genom att välja tre eller fyra av de vinnande numren kan du vinna ett belopp på hundratusentals euro. I det här fallet är dina sannolikheter baserade på att beräkna sannolikheten för att välja ett par korrekta siffror, kombinerat med ett motsatt antal felaktiga siffror. Detta kräver att du först vet det totala antalet möjliga kombinationer. Dessa kan beskrivas med sannolikheten att plocka alla vinnande nummer korrekt.

Du måste först ha beräknat jackpotoddsen enligt beskrivningen i metoden `Beräkna jackpotodds`.
För att förenkla beräkningarna använder vi sannolikheten för att korrekt välja de första fem Powerball-talen. I den andra metoden beräknade vi att detta är 1 av 11.238.513 är.

Bild med titeln Beräkna Lotto-odds Steg 7

2. Skriv ekvationen. Din chans att vinna `k` från antalet `r`-nummer från den totala poolen av nummer `n` kan definieras som:

r! k! (r - k)! \times (n - r)! (r - k)! (n - r - k)! \frac{n!}{r! (n - r)!}

${frac{{frac{r!}{k!(rk)!}}gånger {frac{(no)!}{(rk)!(nrk)!}}}{{frac{n! }{r!(nr)!}}}}$ . Denna formel verkar mycket mer komplicerad, men i verkligheten är den inte mer än tre kopior av den enkla sannolikhetsekvationen från den andra metoden. Fyll bara i dina nummer för n, r och k.

Till exempel, din chans att vinna tre av fem nummer från en pool på 69 beskrivs sedan av ekvationen

5! 3! \times 2! \times 64! 2! \times 61! \frac{69!}{5! \times 64!}

${frac{{frac{5!}{3!times 2!}}times {frac{64!}{2!times 61!}}}{{frac{69!}{5! times 64!}}}}$ .

Bild med titeln Beräkna lottoodds Steg 8

3. Bestäm din chans att vinna. Liksom med grundekvationen löses denna ekvation bäst genom att lägga in det hela i en miniräknare eller sökmotor, eftersom en del av kalkylens mellantal är för stora för att skrivas på. Om det löses rätt blir resultatet sannolikheten att tre av de fem Powerball-numren är rätt valda.

I exemplet blir detta 579,76. Så din chans att korrekt välja tre av fem är 1 på 579,76.

Bild med titeln Beräkna lottoodds Steg 9

4. Välj önskat antal vinnande nummer. Du kan justera din beräkning genom att ändra värdet på k för att bestämma sannolikheten för att vinna olika sekvenser av de fem siffrorna. Din chans att vinna kommer att minska när k blir större och vice versa.

Metod 3 av 3: Beräkna andra lottoodds

Bild med titeln Beräkna Lotto Odds Steg 10

1. Bestäm det förväntade värdet av en lott. Det förväntade värdet på en lott representerar den teoretiska vinsten på en lott. Det är med andra ord summan som du teoretiskt sett skulle kunna få tillbaka efter att ha köpt en lott. Det kan beräknas genom att multiplicera oddsen för en given utbetalning (jackpott, 4 siffror korrekt, 3 siffror korrekta, etc.) med utbetalningsbeloppet och lägg sedan ihop dem. Denna siffra är dock tydligt förvrängd av den enorma jackpotten.

Vanligtvis blir din utbetalning mycket mindre än det förväntade värdet.
Vid standard 5+1 av 69 och 26 Powerball är det förväntade värdet på en biljett ungefär $1,78.

Bild med titeln Beräkna lottoodds steg 11

2. Jämför kostnaden med det förväntade värdet. Du kan fastställa de förväntade fördelarna med att spela på lotteri genom att jämföra det förväntade värdet av en lott med kostnaden för en lott. Vanligtvis blir det mycket mindre. Dessutom skiljer sig din faktiska vinst mycket från det förväntade värdet, trots namnet. De flesta får bara en bråkdel av det idealiska förväntade värdet, om de får något alls.

Vissa lotterier betalar dock mer än andra.

Till exempel, vid ett tillfälle hade lotteriet på $1 från New York Take Five-lotteriet ett förväntat värde lika med kostnaden. Detta innebar att genom att spela detta lotteri kunde spelare förvänta sig att inte förlora.

Bild med titeln Beräkna lottoodds steg 12

3. Bestäm chansökningen genom att spela flera gånger. Att spela på lotteri flera gånger kan öka din genomsnittliga vinstchans, hur lite som helst. Det är lättare att föreställa sig denna ökning som en minskning av din chans att förlora. Till exempel, om din genomsnittliga chans att vinna är 1 på 250.000.000, då är din sannolikhet att förlora oavgjort

249.999.999 \div 250.000.000

$249.999.999div 250.000.000$ , och det är lika med ett tal mycket nära 1 (0,99999...). Om du spelar två gånger blir talet kvadratiskt (

(249.999.999 \div 250.000.000) 2

$(249.999.999div 250.000.000)^{{2}}$ ), vilket skapar ett något lägre nummer än 1 (och därför en större chans att vinna).

Bild med titeln Beräkna lottoodds steg 13

4. Hitta antalet gånger du måste spela för att ha en bra chans att vinna. De flesta lotterispelare är övertygade om att om de spelar tillräckligt ofta kan de öka sina vinstchanser avsevärt. Det är sant att genom att spela oftare har du större chans att vinna. Denna ökning är dock inte betydande länge. Till exempel, givet ovanstående odds (1 på 250 miljoner per spel), måste du spela cirka 180 miljoner gånger för att ha 50-50 chans att vinna.

Med andra ord: köper du tio lotter om dagen har du 50 procents chans att vinna om du köper dessa 49.Fortsätt göra 300 år.

Detta betyder dock inte att ett köp av två biljetter den dagen skulle garantera en vinst. Din totala chans att vinna är fortfarande cirka 50 procent.

Tips

Fall inte för lotteribedrägerier där någon påstår sig ha ett garanterat sätt att vinna. Om någon hade ett garanterat sätt att vinna skulle de verkligen inte stoppa sig själva genom att berätta för dig.
Alla taluppsättningar har exakt samma sannolikheter som alla andra uppsättningar. 32-45-22-19-09-11 är därför lika troligt som 1-2-3-4-5-6.

Varningar

Om du tror att du har ett spelproblem har du förmodligen det. Anonyma spelare är en bra källa till information och hjälp för personer som har att göra med spelberoende.
Spela inte mer än du har råd att förlora.

"Beräkna lottoodds"

Beräkna det geometriska medelvärdet

Beräkna standardavvikelsen

Beräkna rabatten på en produkt

Beräkna volymen av en kub

Оцените, пожалуйста статью