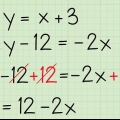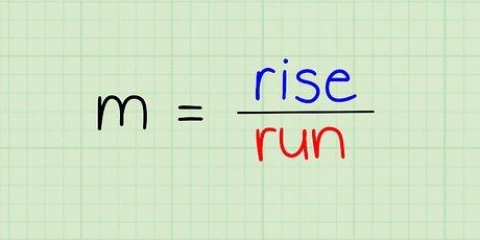Poäng är lätta att avgöra om du har ritat en linje på millimeterpapper. För att bestämma en punkt, rita en prickad linje upp från den horisontella axeln tills den skär linjen. Positionen där du startade linjen på den horisontella axeln är x-koordinaten, medan y-koordinaten är där den prickade linjen skär linjen på den vertikala axeln. Till exempel: linje l har punkterna (1, 5) och (-2, 4) medan linje r har poängen (3, 3) och (1, -4). 
Till linjens lutning l att beräkna: lutning = (5 - (-4))/(1 - (-2)) Subtrahera: lutning = 9/3 Dela: lutning = 3 Linjens lutning r = (3 - (-4))/(3 - 1) = 7/2 
I det här exemplet är 3 inte lika med 7/2, så dessa två linjer är inte parallella. 

Till exempel: Skriv om raden 4y-12x=20 som lutningsformel. Lägg till 12x på båda sidor av ekvationen: 4y - 12x + 12x = 20 + 12x Dividera varje sida med 4 för att isolera y: 4y/4 = 12x/4 +20/4 Lutningsformel: y = 3x + 5 
I vårt exempel har den första raden ekvationen y = 3x + 5, så lutningen är 3. Den andra linjen har ekvationen y = 3x - 1 som också har en lutning på 3. Eftersom lutningarna är identiska är dessa två linjer parallella. Observera att om dessa ekvationer har samma skärningspunkt med y-axeln, skulle de vara samma linje istället för parallella. 

Linjen vi vill göra parallell är y = -4x + 3. I denna ekvation representerar -4 variabeln m och därmed linjens lutning. 
I vårt exempel använder vi koordinaten (1, -2). 
Med vårt exempel med lutning (m) -4 och (x, y) koordinater (1, -2) blir detta: y – (-2) = -4(x – 1) 
Till exempel: y - (-2) = -4(x - 1) Två negativa ger ett positivt: y + 2 = -4(x -1) Använd fördelningsegenskapen för att beräkna -4(x -1): y + 2 = -4x + 4. Subtrahera -2 från båda sidor: y + 2 - 2 = -4x + 4 - 2 Den förenklade ekvationen: y = -4x + 2
Bestäm om två linjer är parallella
Parallella linjer är två linjer i ett plan som aldrig kommer att skära varandra (vilket betyder att de kommer att fortsätta för evigt utan att någonsin röra dem). En viktig egenskap hos parallella linjer är att de har identiska sluttningar. En linjes lutning definieras som stigningen (ändring i y-koordinater) över fallet (ändring i x-koordinater) för en linje, med andra ord hur brant linjen är. Parallella linjer representeras ofta av två vertikala linjer (ll). Till exempel anger AB11CD att linjen AB är parallell med CD.
Steg
Metod 1 av 3: Jämför lutningen för varje linje

1. Hitta formeln för lutningen. Lutningen (lutningen) för en linje definieras av (Y2 - Y1)/(X2 - X1) där X och Y är de horisontella och vertikala koordinaterna för punkter på linjen. Du måste bestämma två punkter på linjen för att beräkna denna formel. Punkten närmare botten av raden är (X1, Y1) och punkten högre upp på linjen, ovanför den första punkten, är (X2, Y2).
- Denna formel kan omformuleras som ökningen över avståndet. Det är den vertikala förändringen jämfört med den horisontella förändringen, eller linjens branthet.
- Om en linje pekar åt höger och uppåt kommer den att ha en positiv lutning.
- Om linjen pekar åt höger och nedåt kommer den att ha en negativ lutning.

2. Identifiera X- och Y-koordinaterna för två punkter på varje linje. En punkt på en linje ges av dess koordinat (X, Y) där X är platsen på den horisontella axeln och Y är platsen på den vertikala axeln. För att beräkna lutningen måste du bestämma två punkter på var och en av linjerna i fråga.

3. Bearbeta punkterna för varje linje i lutningsformeln. För att beräkna lutningen, skriv in siffrorna, subtrahera och dividera. Se till att du infogar koordinaterna i rätt x- och y-värde i formeln.

4. Jämför lutningarna för varje linje. Kom ihåg att två linjer bara är parallella om de har samma lutning. Linjer kan visas parallella på papper och till och med vara mycket nära parallella, men om deras lutningar inte är exakt lika är de inte parallella.
Metod 2 av 3: Använd formeln för lutning och skärningspunkt

1. Hitta formeln för lutning och skärningspunkt för en linje. Lutningsformeln, ekvationen för en rät linje. är y = mx + b, där m är lutningen, b är skärningspunkten med y-axeln och x och y är variabler som representerar koordinater på linjen -- vanligtvis ser du dem som x och y i ekvationen. I det här formuläret kan du enkelt bestämma linjens lutning som variabeln `m`.
- Ett exempel: skriv om 4y - 12x = 20 och y = 3x -1. Ekvationen 4y - 12x = 20 måste skrivas om med algebra medan y = 3x -1 redan har formen av lutningsformeln och behöver inte skrivas om.

2. Skriv om linjens formel som lutningsformel. Ofta kommer formeln för linjen du får inte att vara i form av ett lutande plan. Det krävs bara lite matematisk och variabel omarrangering för att få den till formen för lutningsformeln.

3. Jämför lutningarna för varje linje. Kom ihåg att om två linjer är parallella med varandra kommer de att ha exakt samma lutning. Med hjälp av ekvationen y = mx + b, där m är linjens lutning, kan du bestämma och jämföra lutningarna för två linjer.
Metod 3 av 3: Bestämma en parallell linje med punkt-lutningsekvationen

1. Definiera punkt-lutningsekvationen. Med punkt-lutningsekvationen kan du skriva ekvationen för en linje om du känner till lutningen och har en (x, y) koordinat. Du använder denna formel om du vill definiera en andra parallell linje på en redan given linje med en viss lutning. Formeln är y – y1= m(x – x1) där m är linjens lutning, x1 x-koordinaten för en given punkt på linjen och y1 y-koordinaten för den punkten. Precis som i lutningsformeln är x och y variabler som representerar koordinater på linjen -- i allmänhet kommer de att förbli som x och y i ekvationen.
- Följande steg räkna ut detta exempel: Skriv ekvationen för en linje parallell med linjen y = -4x + 3 som går genom punkt (1, -2).

2. Hitta lutningen på den första raden. När du skriver ekvationen för en ny linje måste du först bestämma lutningen på den linje som din linje måste vara parallell med. Se till att ekvationen för den ursprungliga linjen är en lutningsformel så att du vet lutningen (m) direkt.

3. Identifiera en punkt på den nya linjen. Denna ekvation fungerar bara om du har en koordinat som går genom den nya linjen. Se till att inte välja en koordinat som är på den ursprungliga linjen. Om dina slutliga ekvationer har samma y-skärning, är de inte parallella, utan samma linje.

4. Skriv ekvationen för den nya linjen i punkt-lutningsformen. Kom ihåg att formeln är: y – y1= m(x – x1). Ange lutningen och koordinaterna för din punkt för att göra ekvationen för din nya linje parallell med den första.

5. Förenkla ekvationen. När du har fyllt i siffrorna kan ekvationen förenklas till den vanligare lutningsformeln. Linjen i denna ekvation, när den ritas i ett koordinatsystem, är parallell med den givna ekvationen.
"Bestäm om två linjer är parallella"
Оцените, пожалуйста статью