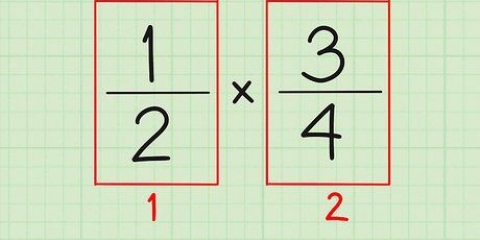
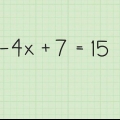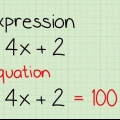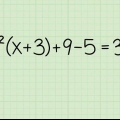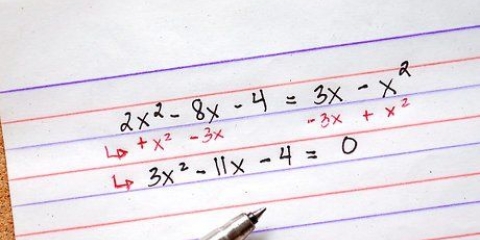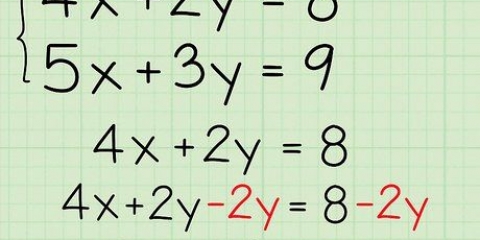....(originalproblem)
....(originalproblem) .... (lägg till 6 på båda sidor)
.... (lägg till 6 på båda sidor) .... (Variabel vänster; konstant höger)
.... (Variabel vänster; konstant höger)
 ....(originalproblem)
....(originalproblem) ....(diva båda sidor med 2)
....(diva båda sidor med 2) ....(lösning)
....(lösning)

 ....(originalproblem)
....(originalproblem) ....(lägg till 36 på varje sida)
....(lägg till 36 på varje sida) ....(förenkla tillägget för att isolera variabeln)
....(förenkla tillägget för att isolera variabeln)
 ....(originalproblem)
....(originalproblem) ....(diva båda sidor med 12)
....(diva båda sidor med 12) ....(lösning)
....(lösning)
Tänk till exempel på problemet,  . För att se till att du distribuerade minustecknet korrekt, skriv om problemet så här:
. För att se till att du distribuerade minustecknet korrekt, skriv om problemet så här: 
Sedan fördelar du -1 över termerna inom parentes, enligt följande:  ....(ändrat problem)
....(ändrat problem) ....(multiplicera -1 med x och med 2)
....(multiplicera -1 med x och med 2) ....(kombinera termer)
....(kombinera termer) ....(lägg till 2 på båda sidor)
....(lägg till 2 på båda sidor) ....(förenkla termer)
....(förenkla termer) ....(diva båda sidor med 3)
....(diva båda sidor med 3) ....(lösning)
....(lösning)


 ....(ursprunglig ekvation)
....(ursprunglig ekvation) ....(tillämpa parenteser)
....(tillämpa parenteser) ....(multiplicera båda sidor med kgf)
....(multiplicera båda sidor med kgf) ....(fördelad multiplikation)
....(fördelad multiplikation) ....(förenkla multiplikation)
....(förenkla multiplikation)
 ....(förenklat problem)
....(förenklat problem) ....(subtrahera 2x från båda sidor)
....(subtrahera 2x från båda sidor) ....(förenkla minussumma)
....(förenkla minussumma) ....(lägg till 18 på båda sidor)
....(lägg till 18 på båda sidor) ....(förenkla tillägg)
....(förenkla tillägg)
 ....(anpassad fråga)
....(anpassad fråga) ....(diva båda sidor med 4)
....(diva båda sidor med 4) ....(Slutgiltig lösning)
....(Slutgiltig lösning)

 .....(anpassad fråga)
.....(anpassad fråga) .....(förenkla bråken)
.....(förenkla bråken)
 .....(anpassad fråga)
.....(anpassad fråga) .....(subtrahera 4 från båda sidor)
.....(subtrahera 4 från båda sidor) .....(isolera x på ena sidan)
.....(isolera x på ena sidan)
 .....(anpassad fråga)
.....(anpassad fråga) .....(diva båda sidor med 2)
.....(diva båda sidor med 2) .....(lösning)
.....(lösning)
 .....(originalproblem)
.....(originalproblem) .....(endast 4x delas med 2, istället för hela räknaren)
.....(endast 4x delas med 2, istället för hela räknaren)

 ..... (fel lösning)
..... (fel lösning)
Börja med lösning x=0:  .....(originalproblem)
.....(originalproblem) .....(ersätt x med 0)
.....(ersätt x med 0)

 .....(Sann. Detta är den rätta lösningen.)
.....(Sann. Detta är den rätta lösningen.)Prova "fel lösning för x=-2:  .....(originalproblem)
.....(originalproblem) .....(skriv in -2 för x)
.....(skriv in -2 för x)

 .....(Felaktigt påstående. Därför är x=-2 falskt.)
.....(Felaktigt påstående. Därför är x=-2 falskt.)
Använda den fördelande egenskapen för att lösa en ekvation
Den fördelande egenskapen är en regel i matematik för att förenkla en ekvation med parenteser. Du lärde dig säkert tidigt att du måste göra operationerna inom parentes först, men med algebraiska uttryck är det inte alltid möjligt. Den fördelande egenskapen låter dig multiplicera termen utanför parentes med termerna inuti den. Du måste vara noga med att du gör det på rätt sätt, annars kan du förlora information och jämförelsen stämmer inte längre. Du kan också använda den fördelande egenskapen för att förenkla ekvationer med bråk.
Steg
Metod 1 av 4: Använda den grundläggande fördelningsegenskapen

1. Multiplicera termen utanför parentes med valfri term inom parentes. För att göra detta delar du i huvudsak den yttre termen mellan de inre termerna. Multiplicera termen utanför parentes med den första termen inom parentes. Sedan multiplicerar du det med den andra termen. Om det finns fler än två termer, fortsätt att fördela termen utanför parentesen över alla termer inom parentesen. Lämna bara operatorerna (plus eller minus) inom parentes.

2. Kombinera liknande termer. Innan du kan lösa ekvationen måste du kombinera lika termer. Kombinera alla numeriska termer med varandra. Dessutom kombinerar du alla variabeltermer separat. För att förenkla ekvationen, ordna termerna så att variablerna finns på ena sidan av likhetstecknet och konstanterna (endast talen) på den andra sidan.
 ....(originalproblem)
....(originalproblem) .... (lägg till 6 på båda sidor)
.... (lägg till 6 på båda sidor) .... (Variabel vänster; konstant höger)
.... (Variabel vänster; konstant höger)
3. Lös ekvationen. lösa  genom att dividera båda sidor av ekvationen med koefficienten för variabeln.
genom att dividera båda sidor av ekvationen med koefficienten för variabeln.
 genom att dividera båda sidor av ekvationen med koefficienten för variabeln.
genom att dividera båda sidor av ekvationen med koefficienten för variabeln. ....(originalproblem)
....(originalproblem) ....(diva båda sidor med 2)
....(diva båda sidor med 2) ....(lösning)
....(lösning)Metod 2 av 4: Fördela negativa koefficienter

1. Fördela ett negativt tal tillsammans med minustecknet. Om du ska multiplicera en term eller termer inom parentes med ett negativt tal, se till att använda minustecknet på varje term inom parentesen. Titta på följande exempel:  .... (originalproblem)
.... (originalproblem) ....(multiplicera -4 med varje term)
....(multiplicera -4 med varje term) ....(förenkla multiplikationen)
....(förenkla multiplikationen) ....(observera att `minus -12` är detsamma som +12)
....(observera att `minus -12` är detsamma som +12)
- Kom ihåg de grundläggande reglerna för att multiplicera med negativa tal:
- Minus x Minus = Plus.
- Minus x Plus = Minus.
 .... (originalproblem)
.... (originalproblem) ....(multiplicera -4 med varje term)
....(multiplicera -4 med varje term) ....(förenkla multiplikationen)
....(förenkla multiplikationen) ....(observera att `minus -12` är detsamma som +12)
....(observera att `minus -12` är detsamma som +12)
2. Kombinera liknande termer. När du har slutfört fördelningen måste du förenkla ekvationen genom att flytta alla variabeltermer till ena sidan av likhetstecknet och alla tal utan variabler till den andra sidan. Detta gör du med hjälp av en kombination av addition eller subtraktion.
 ....(originalproblem)
....(originalproblem) ....(lägg till 36 på varje sida)
....(lägg till 36 på varje sida) ....(förenkla tillägget för att isolera variabeln)
....(förenkla tillägget för att isolera variabeln)
3. Dela för att få den slutgiltiga lösningen. Lös ekvationen genom att dividera båda sidor av ekvationen med variabelns koefficient. Detta bör resultera i en enda variabel på ena sidan av ekvationen, med resultatet på den andra sidan.
 ....(originalproblem)
....(originalproblem) ....(diva båda sidor med 12)
....(diva båda sidor med 12) ....(lösning)
....(lösning)
4. Behandla subtraktion som addition (från -1). När du ser ett minustecken i ett algebraproblem, särskilt om det är före en parentes, står det i huvudsak + (-1). Detta hjälper till att fördela minustecknet korrekt över alla termer inom parentes. Lös sedan problemet som tidigare.
 . För att se till att du distribuerade minustecknet korrekt, skriv om problemet så här:
. För att se till att du distribuerade minustecknet korrekt, skriv om problemet så här:
 ....(ändrat problem)
....(ändrat problem) ....(multiplicera -1 med x och med 2)
....(multiplicera -1 med x och med 2) ....(kombinera termer)
....(kombinera termer) ....(lägg till 2 på båda sidor)
....(lägg till 2 på båda sidor) ....(förenkla termer)
....(förenkla termer) ....(diva båda sidor med 3)
....(diva båda sidor med 3) ....(lösning)
....(lösning)Metod 3 av 4: Använd den fördelande egenskapen för att förenkla bråk

1. Ta reda på om det finns bråkkoefficienter eller konstanter. Ibland kan du behöva lösa ett problem med bråk som koefficienter eller konstanter. Du kan lämna dem som de är och tillämpa de grundläggande algebrareglerna på dem för att lösa problemet. Men genom att använda den fördelande egenskapen kan man ofta förenkla lösningen genom att konvertera bråken till heltal.
- Kolla in följande exempel
. Bråken i detta exempel är
och
.

2. Hitta minsta gemensamma multipel (LCM) för alla nämnare. I detta steg kan du ignorera alla heltal. Titta bara på bråken och bestäm LCF för alla nämnare. Bestäm kgf genom att leta efter det minsta talet som är en multipel av nämnarna för båda bråken i ekvationen. I det här exemplet är nämnarna 3 och 6, så 6 är kgf.

3. Multiplicera alla termer i ekvationen med kgf. Kom ihåg att du kan tillämpa vilken operation som helst på en matematisk ekvation, så länge du gör det på båda sidor. Genom att multiplicera varje term i ekvationen med lcg tar termerna ut varandra och "blir" heltal. Placera dina parenteser runt hela vänster och höger sida av ekvationen och gör sedan fördelningen:
 ....(ursprunglig ekvation)
....(ursprunglig ekvation) ....(tillämpa parenteser)
....(tillämpa parenteser) ....(multiplicera båda sidor med kgf)
....(multiplicera båda sidor med kgf) ....(fördelad multiplikation)
....(fördelad multiplikation) ....(förenkla multiplikation)
....(förenkla multiplikation)
4. Kombinera liknande termer. Kombinera alla termer så att alla variabler finns på ena sidan av ekvationen och alla konstanter på andra sidan. Använd de grundläggande additions- och subtraktionsoperationerna för att flytta termer från ena sidan av ekvationen till den andra.
 ....(förenklat problem)
....(förenklat problem) ....(subtrahera 2x från båda sidor)
....(subtrahera 2x från båda sidor) ....(förenkla minussumma)
....(förenkla minussumma) ....(lägg till 18 på båda sidor)
....(lägg till 18 på båda sidor) ....(förenkla tillägg)
....(förenkla tillägg)
5. Lös ekvationen. Hitta den slutliga lösningen genom att dividera båda sidor av ekvationen med variabelns koefficient. Detta lämnar dig med x på ena sidan av ekvationen och den numeriska lösningen på den andra.
 ....(anpassad fråga)
....(anpassad fråga) ....(diva båda sidor med 4)
....(diva båda sidor med 4) ....(Slutgiltig lösning)
....(Slutgiltig lösning)Metod 4 av 4: Fördela ett bråk med en ekvation

1. Tolka ett bråk med en ekvation som en fördelad division. Ibland ser du ett problem med flera termer i täljaren för ett bråk, ovanför en gemensam nämnare. Du måste behandla detta som ett fördelningsproblem och tillämpa nämnaren på varje term i täljaren. Du kan skriva om bråket för att visa fördelningen. Som följer:
.....(originalproblem)
.....(multiplicera nämnaren med varje term i täljaren)

2. Förenkla varje täljare som separat bråk. Efter att ha fördelat divisorn över varje term kan du sedan förenkla varje term individuellt.
 .....(anpassad fråga)
.....(anpassad fråga) .....(förenkla bråken)
.....(förenkla bråken)
3. Isolera variabeln. Fortsätt lösa problemet genom att isolera variabeln på ena sidan av ekvationen och flytta de konstanta termerna till den andra sidan. Gör detta genom en kombination av addition och subtraktion, vid behov.
 .....(anpassad fråga)
.....(anpassad fråga) .....(subtrahera 4 från båda sidor)
.....(subtrahera 4 från båda sidor) .....(isolera x på ena sidan)
.....(isolera x på ena sidan)
4. Dividera med koefficienten för att lösa problemet. I det sista steget dividerar du med koefficienten för variabeln. Detta ger den slutliga lösningen, med den enskilda variabeln på ena sidan av ekvationen och den numeriska lösningen på den andra.
 .....(anpassad fråga)
.....(anpassad fråga) .....(diva båda sidor med 2)
.....(diva båda sidor med 2) .....(lösning)
.....(lösning)
5. Undvik det vanliga misstaget att bara dela en term. Det är frestande (men felaktigt) att dela den första termen i täljaren med nämnaren och eliminera bråket. Ett fel som detta skulle se ut så här för ovanstående problem:
 .....(originalproblem)
.....(originalproblem) .....(endast 4x delas med 2, istället för hela räknaren)
.....(endast 4x delas med 2, istället för hela räknaren)

 ..... (fel lösning)
..... (fel lösning)
6. Kontrollera att din lösning är korrekt. Du kan alltid kontrollera ditt arbete genom att infoga din lösning i det ursprungliga problemet. När du vill förenkla måste du komma fram till ett sant påstående. Om du förenklar och får ett felaktigt påstående som svar, så är din lösning felaktig. I det här exemplet testar du de två lösningarna för x = 0 och x =-2 för att se vilken som är korrekt.
 .....(originalproblem)
.....(originalproblem) .....(ersätt x med 0)
.....(ersätt x med 0)

 .....(Sann. Detta är den rätta lösningen.)
.....(Sann. Detta är den rätta lösningen.) .....(originalproblem)
.....(originalproblem) .....(skriv in -2 för x)
.....(skriv in -2 för x)

 .....(Felaktigt påstående. Därför är x=-2 falskt.)
.....(Felaktigt påstående. Därför är x=-2 falskt.)Tips
- Du kan också använda den fördelande egenskapen för att förenkla vissa multiplikationer. Du kan dela upp tal i tiotal med en rest för att göra huvudräkningen lättare. Till exempel kan du skriva om 8 x 16 som 8(10+6). Detta är då helt enkelt 80 + 48 = 128. Ett annat exempel, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Öva dessa utantill och huvudräkning kommer att bli mycket lättare.
"Använda den fördelande egenskapen för att lösa en ekvation"
Оцените, пожалуйста статью