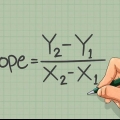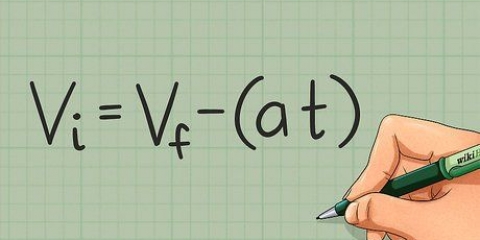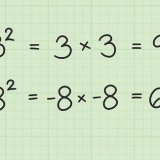Hur man bestämmer exakthet

Steg
Tips

Noggrannhet innebär att en mätning med ett visst verktyg eller instrument ger liknande resultat varje gång det används. Till exempel, om du kliver på en våg fem gånger i rad, ska en exakt våg visa dig samma vikt varje gång. Inom matematik och naturvetenskap är beräkningsnoggrannhet viktigt för att avgöra om dina instrument och mätningar är tillräckligt bra för att få bra data. Du kan representera noggrannheten för varje datamängd med hjälp av värdeintervallet, medelavvikelsen eller standardavvikelsen.

Steg

Metod 1 av 4: Beräkna intervallet

1. Bestäm det högsta uppmätta värdet. Det hjälper att börja sortera dina data i numerisk ordning, från lägsta till högsta. Detta kommer att se till att du inte hoppar över några av värdena. Välj sedan värdet i slutet av listan.

Säg till exempel att du testar noggrannheten på en skala och ser fem avläsningar: 11, 13, 12, 14, 12. Sorterade dessa värden visas som 11, 12, 12, 13, 14. Det högsta värdet är 14.

Bild med titeln Beräkna precision steg 2

2. Bestäm det lägsta uppmätta värdet. När din data är sorterad är det lika enkelt att hitta det lägsta värdet som att titta i början av listan.

Inom vågens mätdata är det lägsta värdet 11.

Bild med titeln Beräkna precision steg 3

3. Subtrahera det lägsta värdet från det högsta. Omfånget för en uppsättning data är skillnaden mellan de högsta och lägsta avläsningarna. Bara subtrahera från varandra. Algebraiskt uttrycks intervallet som:

räckvidd = X (m a X) - X (m i n)

${text{Range}}=x(max)-x(min)$

Omfattningen av exempeldata är:

räckvidd = X (m a X) - X (m i n) = 14 - 11 = 3

${text{Range}}=x(max)-x(min)=14-11=3$

Bild med titeln Beräkna precision steg 4

4. Visa intervallet som noggrannhet. När du rapporterar data är det viktigt att läsarna vet vad du har mätt. Eftersom noggrannhet finns i olika mätvärden måste du ange vad du vill rapportera. För dessa data anger du: medelvärde = 12,4, intervall = 3. Eller helt enkelt: medelvärde = 12,4 ±3.

Medelvärdet är inte nödvändigtvis en del av beräkningsområdet eller noggrannheten, utan är i allmänhet den första beräkningen för att rapportera det uppmätta värdet. Medelvärdet erhålls genom att dividera summan av de uppmätta värdena med antalet objekt i gruppen. Medelvärdet för denna dataserie är (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Metod 2 av 4: Beräkning av medelavvikelse

Bild med titeln Beräkna precision steg 5

1. Bestäm först genomsnittet av data. Medelavvikelsen är ett mer detaljerat mått på precisionen för en grupp mätningar eller värden för ett experiment. Det första steget för att hitta medelavvikelsen är att beräkna medelvärdet av de uppmätta värdena. Medelvärdet är summan av värdena dividerat med antalet mätningar.

I det här exemplet använder vi samma exempeldata som tidigare. Antag att fem mätningar har gjorts, 11, 12, 13, 14 och 12. Medelvärdet av dessa värden är (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Bild med titeln Beräkna precision steg 6

2. Beräkna den absoluta avvikelsen för varje värde från medelvärdet. För denna beräkning av precision måste du bestämma hur nära varje värde är medelvärdet. För att göra detta, subtrahera medelvärdet av varje tal. För denna mätning spelar det ingen roll om värdet är över eller under genomsnittet. Subtrahera siffrorna och använd bara det positiva värdet av resultatet. Detta är också känt som det "absoluta värdet".

Algebraiskt representeras det absoluta värdet genom att placera två vertikala staplar runt beräkningen. Som följer:

Absolut avvikelse = | X - μ |

${text{Absolut avvikelse}}=|x-mu |$

Denna beräkning säger

X

$X$ för vart och ett av experimentvärdena och

μ

$mu$ för det beräknade genomsnittet.

När det gäller värdena för provdataserien är de absoluta avvikelserna:

| 12 - 12, 4 | = 0, 4

$|12-12,4|=0,4$

| 11 - 12, 4 | = 1, 4

$|11-12.4|=1.4$

| 14 - 12, 4 | = 1, 6

$|14-12.4|=1.6$

| 13 - 12, 4 | = 0, 6

$|13-12,4|=0,6$

| 12 - 12, 4 | = 0, 4

$|12-12,4|=0,4$

Bild med titeln Beräkna precision steg 7

3. Bestäm medelavvikelsen. Använd de absoluta avvikelserna och hitta deras medelvärde. Som med den ursprungliga uppsättningen av data lägger du ihop värdena och dividerar summan med antalet värden. Detta representeras algebraiskt som:

Genomsnittlig avvikelse = Σ | X - μ | n

${text{Mean Deviation}}={frac{Sigma |x-mu |}{n}}$

När det gäller dessa exempeldata går beräkningen så här:

Genomsnittlig avvikelse = 0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4 5

${text{Medelavvikelse}}={frac{0.4+1.4+1.6+0.6+0.4}{5}}$

Genomsnittlig avvikelse = 4, 4 5

${text{Medelavvikelse}}={frac{4,4}{5}}$

Genomsnittlig avvikelse = 0, 88

${text{Medelavvikelse}}=0,88$

Bild med titeln Beräkna precision steg 8

4. Ange resultatet av noggrannheten. Detta resultat kan rapporteras som medelvärde, plus eller minus medelavvikelsen. För denna exempeldatauppsättning ser detta ut som 12,4 ±0,88. Observera att om noggrannheten anges som medelavvikelse får mätningen att verka mycket mer exakt än med intervallet.

Metod 3 av 4: Beräkna standardavvikelsen

Bild med titeln Beräkna precision steg 9

1. Använd rätt formel för standardavvikelsen. För vilken datamängd som helst är standardavvikelsen en tillförlitlig statistik för att visa precision. Det finns två formler för att beräkna standardavvikelsen, med en mycket liten skillnad mellan dem. Du använder en formel om dina mätvärden täcker en hel population. Den andra formeln används om de uppmätta data endast är ett urval av populationen.

Din data representerar en hel population om du har samlat in alla möjliga mått från alla möjliga ämnen. Till exempel, om du testar personer med en mycket sällsynt sjukdom, och du är säker på att du har testat alla med denna sjukdom, inkluderar detta hela befolkningen. Formeln för standardavvikelsen i detta fall är:

$Σ = \sqrt{} Σ (X - μ) 2 n$ $sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n}}}}$

Ett urval är en datagrupp som är mindre än en hel population. Du kommer vanligtvis att använda den här mest. Standardavvikelsens formel för ett prov är:

Σ = \sqrt{} Σ (X - μ) 2 n - 1

$sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n-1}}}}$

Observera att den enda skillnaden är bråkets nämnare. För en full befolkning, dividera med

n

$n$ . Om du har ett prov, vänligen dela

n - 1

$n-1$ .

Bild med titeln Beräkna precision steg 10

2. Hitta medelvärdet av datavärdena. Precis som vid beräkningen av medelavvikelsen börjar man med att bestämma medelvärdet av datavärdena.

Med samma uppsättning avläsningar som noterats ovan är medelvärdet 12,4.

Bild med titeln Beräkna precision steg 11

3. Hitta kvadraten på varje variant. För varje datapunkt subtraherar du datavärdet från medelvärdet och kvadrerar resultatet. Eftersom du kvadrerar dessa variationer spelar det ingen roll om skillnaden är positiv eller negativ. Skillnadens kvadrat är alltid positiv.

För de fem datavärdena i detta exempel går dessa beräkningar ut så här:

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

(11 - 12, 4) 2 = (- 1, 4)^{2} = 1, 96

$(11-12,4)^{2}=(-1,4)^{2}=1,96$

(14 - 12, 4) 2 = 1, 6^{2} = 2, 56

$(14-12,4)^{2}=1,6^{2}=2,56$

(13 - 12, 4) 2 = 0, 6^{2} = 0, 36

$(13-12,4)^{2}=0,6^{2}=0,36$

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

Bild med titeln Beräkna precision steg 12

4. Beräkna summan av skillnaderna i kvadrat. Täljaren för bråket i standardavvikelsen är summan av de kvadratiska skillnaderna mellan värdena och medelvärdet. Du kan bestämma detta belopp genom att lägga till siffrorna från föregående beräkning tillsammans.

För exempeldatauppsättningen är dessa:

0, 16 + 1, 96 + 2, 56 + 0, 36 + 0, 16 = 5, 2

$0,16+1,96+2,56+0,36+0,16=5,2$

Bild med titeln Beräkna precision steg 13

5. Dela efter datastorlek. Detta är det enda steget som är annorlunda i en populationsberäkning jämfört med ett urval. För en komplett population dividerar man med

n

$n$ (antal värden). I ett prov dividerar man med

n - 1

$n-1$ .

Följande exempel har endast fem mätningar och är därför endast ett prov. Så för de fem värdena som används, dividera med (5 - 1) eller 4. Resultatet är

5, 2 / 4 = 1, 3

$5,2/4=1,3$ .

Bild med titeln Beräkna precision steg 14

6. Hitta kvadratroten av resultatet. Vid denna tidpunkt representerar beräkningen vad som kallas datauppsättningens varians. Standardavvikelsen är kvadratroten av variansen. Använd en miniräknare för att hitta kvadratroten och med den standardavvikelsen.

Σ = \sqrt{1.3} = 1, 14

$sigma ={sqrt{1.3}}=1,14$

Bild med titeln Beräkna precision steg 15

7. Visa ditt resultat. Med hjälp av denna beräkning kan skalans precision anges genom att ange medelvärdet plus eller minus standardavvikelsen. För dessa data blir det 12,4 ±1,14.

Standardavvikelsen är kanske det vanligaste måttet på precision. Men för tydlighetens skull är det fortfarande en bra idé att använda en fotnot eller parentes för att indikera att precisionsvärdet representerar standardavvikelsen.

Metod 4 av 4: Bestäm hur noggrannhet ska anges

Bild med titeln Beräkna precision steg 16

1. Använd ordet noggrannhet korrekt. Noggrannhet är en term som används för att indikera repeterbarheten av mätningar. Om du samlar in en grupp data, antingen genom mätning eller genom ett visst experiment, beskriver noggrannheten hur nära varandra resultaten av varje mätning eller experiment kommer att vara.

Noggrannhet är inte detsamma som noggrannhet. Noggrannhet mäter hur nära experimentella värden är det faktiska eller teoretiska värdet medan noggrannhet mäter hur nära de uppmätta värdena är varandra.
Data kan vara korrekt men inte korrekt eller korrekt men inte korrekt. Noggranna avläsningar kan vara nära målet, men kanske inte nära varandra. Noggranna avläsningar ligger nära varandra oavsett om de är nära målvärdena eller inte.

Bild med titeln Beräkna precision steg 17

2. Välj den bästa graden av noggrannhet. Ordet "noggrannhet" har inte en enda betydelse. Det är möjligt att visa noggrannhet med flera olika mätningar. Du måste bestämma vilken som är bäst.

Räckvidd. För små datamängder med cirka tio eller färre mätningar är värdeintervallet ett bra mått på noggrannhet. Detta gäller särskilt om värdena är grupperade ganska nära varandra. Om du upptäcker att ett eller två värden är långt ifrån de andra värdena, bör du förmodligen använda en annan beräkning.

Genomsnittlig avvikelse. Medelavvikelsen är ett mer exakt mått på noggrannheten hos en liten uppsättning datavärden.

standardavvikelse. Standardavvikelsen är kanske det mest kända måttet på noggrannhet. Standardavvikelse kan användas för att beräkna noggrannheten av mätningarna för en hel population eller ett urval av populationen.

Bild med titeln Beräkna precision steg 18

3. Ge en tydlig representation av dina resultat. Mycket ofta kommer forskare att rapportera data genom att ange medelvärdet av det uppmätta värdet följt av graden av noggrannhet. Noggrannheten visas med symbolen `±`. Detta ger en indikation på noggrannhet, men det förklarar inte tydligt för läsaren om siffran efter `±`-symbolen är ett intervall, standardavvikelse eller något annat mått. För att tydliggöra detta måste du definiera vilken noggrannhetsnivå du har använt, antingen i en fotnot eller som en kommentar inom parentes.

För en given dataserie kan resultatet visas som 12,4 ±3. Ett mer beskrivande sätt att ange samma data skulle dock vara detta: `Mean = 12,4, Range = 3.`

Tips

Om ett av värdena i urvalet är mycket högre eller lägre än resten av dina värden, exkludera inte detta värde från dina beräkningar. Även om det var ett misstag förblir det data och måste användas för korrekt beräkning.
Endast fem värden användes i den här artikeln för matematisk enkelhet. I ett faktiskt experiment bör du använda mer än fem mätvärden för en mer exakt beräkning. Ju fler prover du kör, desto mer exakt.

"Bestäm noggrannhet"

Bestäm dimensioner

Bestäm om två linjer är parallella

Bestäm atomnumret för ett grundämne

Bestäm nettoeffekt

Оцените, пожалуйста статью