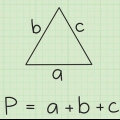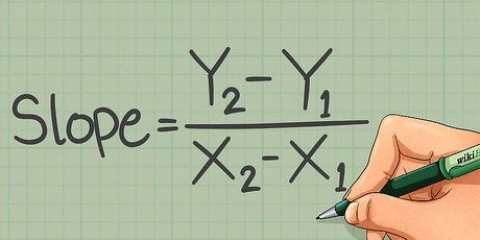Hur man avgör om tre längder tillsammans bildar en triangel: 6 steg (med bilder)

Steg
Tips

Att avgöra om längderna av tre sidor tillsammans bildar en triangel är lättare än det ser ut. Allt du behöver göra är att använda triangelolikhetssatsen, som säger att summan av längderna på två sidor i en triangel alltid är större än den tredje sidan. Om detta gäller alla tre kombinationerna av de tillagda längderna, så har du att göra med en triangel.

Steg

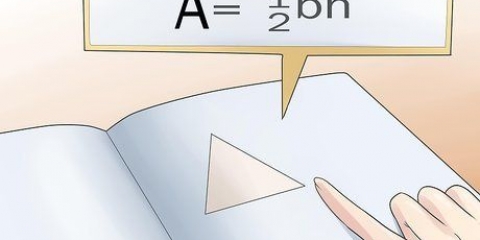
1. Lär dig satsen om triangelojämlikheten. Denna sats säger att summan av två sidor i en triangel måste vara större än den tredje sidan. Om detta gäller alla tre kombinationerna, så har du en sann triangel. Du måste kontrollera dessa kombinationer, en efter en, för att säkerställa att en triangel kan bildas. Du kan också betrakta triangeln som sidorna av längderna a, b och c, och satsen som olikhet: a+b > c, a+c > b och b+c > a.

Ett exempel, a = 7, b = 10 och c = 5.

Bild med titeln Bestäm om tre sidlängder är en triangel Steg 2

2. Kontrollera om summan av de två första sidorna är större än den tredje. I det här fallet kan du använda sidorna a och b lägg ihop, dvs 7 + 10, för att få 17, vilket är större än 5. Du kan också tänka på det som 17 > 5.

Bild med titeln Bestäm om tre sidlängder är en triangel Steg 3

3. Kontrollera om summan av nästa kombination av två sidor är större än den återstående sidan. Tja, se bara om summan av sidorna a och c är större än sidan b. Det betyder att du måste se om 7 + 5, eller 12, är större än 10. 12 > 10, så det stämmer.

Bild med titeln Bestäm om tre sidlängder är en triangel Steg 4

4. Kontrollera om summan av den sista kombinationen av två sidor är större än den återstående sidan. Du måste kontrollera om summan av sidor b och siden c är större än silke a. För att göra detta måste du kontrollera om 10 + 5 är större än 7. 10 + 5 = 15 och 15 > 7, så triangeln är korrekt för alla sidor.

Bild med titeln Bestäm om tre sidlängder är en triangel Steg 5

5. Kontrollera ditt arbete. Nu när du har markerat alla sidor en efter en kan du kontrollera igen att regeln gäller alla tre kombinationerna. Om summan av en av de två sidorna är större än den tredje i någon kombination, som med denna triangel, har du bestämt att triangeln är giltig. Om regeln inte gäller för ens en kombination, är det inte en sann triangel. Eftersom följande påståenden är sanna har du hittat en giltig triangel:

a + b > c = 17 > 5

a + c > b = 12 > 10

b + c > a = 15 > 7

Bild med titeln Bestäm om tre sidlängder är en triangel Steg 6

6. Vet hur man tar reda på en ogiltig triangel. Bara för att få kläm på det, men du måste se till att du kan se en triangel som inte stämmer. Anta att du har att göra med följande tre sidor och längderna: 5, 8 och 3. Låt oss se om de klarar testet:

5 + 8 > 3 = 13 > 3, så denna sida är korrekt.

5 + 3 > 8 = 8 > 8. Eftersom det här inte är rätt kan du sluta nu. Det här är inte en triangel.