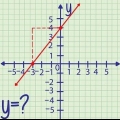
Beräkna skärningspunkten mellan två linjer (med bilder)

Steg
- Metod 1 av 2: Bestämma skärningspunkten mellan två räta linjer
- Metod 2 av 2: Problem med andragradsekvationer
Tips

När räta linjer skär varandra på en tvådimensionell graf, gör de det vid endast en punkt, indikerad av koordinaterna x och y. Eftersom båda linjerna passerar genom den punkten vet du att x- och y-koordinaterna måste uppfylla båda ekvationerna. Med några extra tekniker kan du hitta skärningspunkterna för paraboler och andra kvadratiska kurvor, med samma logik.

Steg

Metod 1 av 2: Bestämma skärningspunkten mellan två räta linjer

1. Skriv ekvationen för valfri linje med y till vänster. Om det behövs, ändra ekvationen så att y isoleras på ena sidan av likhetstecknet. Om ekvationen skrivs med f(x) eller g(x) istället för y, separera den termen. Kom ihåg att du kan eliminera termer genom att utföra samma operation på båda sidor.

Är ekvationerna okända, bestäm sedan det baserat på den information som ges.
Exempel: Anta att du har två rader $y = X + 3$ $y=x+3$ och $y - 12 = - 2 X$ $y-12=-2x$ . För att separera y i den andra ekvationen, lägg till 12 på varje sida: $y = 12 - 2 X$ $y=12-2x$

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 2

2. Se till att de högra sidorna av ekvationerna är lika. Vi letar efter en punkt där de två linjerna har samma x- och y-värden; detta är punkten där linjerna skär varandra. Båda ekvationerna har bara ett y till vänster, så vi vet att de högra sidorna är lika med varandra. Skriv en ny ekvation som visar detta.

Exempel: vi vet det

y = X + 3

$y=x+3$ och

y = 12 - 2 X

$y=12-2x$ , och sålunda $X + 3 = 12 - 2 X$ $x+3=12-2x$ .

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 3

3. Lös x i ekvationen. Den nya ekvationen har bara en variabel, x. Lös detta med algebra, genom att utföra samma operation på båda sidor. Hitta x-termerna på varje sida av ekvationen och placera dem i formen x = __ (om det inte är möjligt, fortsätt att läsa i slutet av det här avsnittet).

Exempel:

X + 3 = 12 - 2 X

$x+3=12-2x$

telefon

2 X

$2x$ på varje sida:

3 X + 3 = 12

$3x+3=12$

Subtrahera 3 från varje sida:

3 X = 9

$3x=9$

Dela varje sida med 3:

X = 3

$x=3$ .

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 4

4. Använd detta x-värde för att lösa för y. Välj ekvationen för varje linje. Byt ut varje x i ekvationen med svaret du hittade. Lös nu för y.

Exempel:

X = 3

$x=3$ och

y = X + 3

$y=x+3$

y = 3 + 3

$y=3+3$

y = 6

$y=6$

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 5

5. Kontrollera ditt arbete. Det är klokt att plugga in ditt x-värde i den andra ekvationen för att se om du får samma resultat. Om du får en annan lösning för y, gå tillbaka och kontrollera ditt arbete för fel.

Exempel:

X = 3

$x=3$ och

y = 12 - 2 X

$y=12-2x$

y = 12 - 2 (3)

$y=12-2(3)$

y = 12 - 6

$y=12-6$

$y = 6$ $y=6$

Detta är samma svar som tidigare erhållits. Vi gjorde inga misstag.

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 6

6. Skriv ner x- och y-koordinaterna för skärningspunkten. Du har nu löst x-värdet och y-värdet för skärningspunkten mellan de två linjerna. Skriv punkten som en koordinat, med x-värdet som första tal.

Exempel:

X = 3

$x=3$ och

y = 6

$y=6$

De två linjerna skär varandra i punkten (3.6).

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 7

7. Bearbeta ovanliga resultat. Vissa ekvationer gör det omöjligt att lösa x. Detta betyder inte nödvändigtvis att du har gjort ett misstag. Det finns två sätt på vilka ett par linjer kan leda till en speciell lösning:

Om de två linjerna är parallella kommer de inte att skära varandra . X-termerna kan elimineras och din ekvation kan förenklas till en ogiltig ekvation (som t.ex

0 = 1

$0=1$ ). Notera här`linjerna skär inte varandra eller inte en giltig lösning" om du svarar.

Om de två ekvationerna beskriver samma linje, så "skär" de varandra överallt. Du kan eliminera x-termerna och förenkla din ekvation till en giltig ekvation (som t.ex

3 = 3

$3=3$ ). Skriv ner `de två linjerna är samma" som ett svar.

Metod 2 av 2: Problem med andragradsekvationer

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 8

1. Lär dig känna igen andragradsekvationer. I en andragradsekvation finns en eller flera variabler i andragradsform (

X 2

$x^{2}$ eller

y 2

$y^{2}$ ), och det finns inga högre makter. Linjerna som representeras av ekvationer är krökta och kan därför skära en rät linje i 0, 1 eller 2 punkter. I den här delen kommer du att lära dig hur du hittar skärningspunkterna för ett sådant problem.

Träna ut ekvationer inom parentes för att se om de är kvadratiska. Till exempel, $y = (X + 3) (X)$ $y=(x+3)(x)$ är kvadratisk, eftersom du kan sätta den utanför parentes om $y = X 2 + 3 X .$ $y=x^{2}+3x$
Att ha ekvationer av en cirkel eller en ellips både a $X 2$ $x^{2}$ som en $y 2$ $y^{2}$ termin. Om du tycker att dessa speciella fall är svåra, läs vidare på Tips i slutet av den här artikeln.

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 9

2. Skriv ekvationerna i termer av y. Om det behövs, skriv om varje ekvation så att y är på ena sidan.

Exempel: Hitta skärningspunkten mellan

X 2 + 2 X - y = - 1

$x^{2}+2x-y=-1$ och

y = X + 7

$y=x+7$ .

Skriv om andragradsekvationen i termer av y:

$y = X 2 + 2 X + 1$ $y=x^{2}+2x+1$ och $y = X + 7$ $y=x+7$ .

Detta exempel har en andragradsekvation och en linjär ekvation. Problem med två andragradsekvationer löses på samma sätt.

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 10

3. Kombinera de två ekvationerna för att eliminera y. Om du har gjort båda ekvationerna lika med y, så vet du att de två ekvationerna utan y är lika med varandra.

Exempel:

y = X 2 + 2 X + 1

$y=x^{2}+2x+1$ och

y = X + 7

$y=x+7$

$X 2 + 2 X + 1 = X + 7$ $x^{2}+2x+1=x+7$

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 11

4. Ordna om den nya ekvationen så att en sida är lika med noll. Använd vanliga matematiska metoder för att få alla termer på ena sidan av ekvationen. Detta är den nödvändiga uppställningen av problemen för att kunna lösa dem i nästa steg.

Exempel:

X 2 + 2 X + 1 = X + 7

$x^{2}+2x+1=x+7$

Subtrahera x från varje sida:

X 2 + X + 1 = 7

$x^{2}+x+1=7$

Subtrahera 7 från varje sida:

$X 2 + X - 6 = 0$ $x^{2}+x-6=0$

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 12

5.Lös andragradsekvationen. Om du har en sida lika med noll finns det tre sätt att lösa andragradsekvationen. Alla föredrar en annan metod. Du kan läsa mer om den kvadratiska formeln för "dela kvadraten", eller så kan du följa det här exemplet vidare för det faktorisera metod:

Exempel:

X 2 + X - 6 = 0

$x^{2}+x-6=0$

Syftet med factoring är att bestämma de två faktorerna multiplicerade tillsammans för att producera denna ekvation. Från och med första terminen vet vi det

X 2

$x^{2}$ kan delas in i x och x. Skriv (x )(x ) = 0 för att visa detta.

Sista terminen är -6. Skriv ner varje par av faktorer som multiplicerats för att ge -6 som produkten:

- 6 * 1

$-6*1$ ,

- 3 * 2

$-3*2$ ,

- 2 * 3

$-2*3$ , och

- 1 * 6

$-1*6$ .

Mellantermen är x (som du kan skriva som 1x). Lägg ihop varje par av faktorer för att få 1 som svar. Rätt par av faktorer är

- 2 * 3

$-2*3$ , eftersom

- 2 + 3 = 1

$-2+3=1$ .

Fyll i luckorna i ditt svar med dessa få faktorer: $(X - 2) (X + 3) = 0$ $(x-2)(x+3)=0$ .

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 13

6. Håll ögonen öppna för två lösningar för x. Om du arbetar för snabbt kan du hitta ett svar på problemet utan att inse att det finns ett annat. Så här hittar du de två x-värdena för linjer som skär varandra i två punkter:

Exempel (faktor): Vi slutar med ekvationen

(X - 2) (X + 3) = 0

$(x-2)(x+3)=0$ . Om båda faktorerna inom parentes är lika med 0, är ekvationen sann. Den ena lösningen är

X - 2 = 0

$x-2=0$ → $X = 2$ $x=2$ . Den andra lösningen är

X + 3 = 0

$x+3=0$ → $X = - 3$ $x=-3$ .

Exempel (kvadratisk ekvation eller kvadratisk kvadrat): Om du använder någon av dessa metoder för att lösa ekvationen kommer en kvadratrot att visas. Till exempel blir vår ekvation

X = (- 1 + \sqrt{25}) / 2

$x=(-1+{sqrt{25}})/2$ . Kom ihåg att du kan förenkla en kvadratrot till två olika lösningar:

\sqrt{25} = 5 * 5

${sqrt{25}}=5*5$ , och

\sqrt{25} = (- 5) * (- 5)

${sqrt{25}}=(-5)*(-5)$ . Skriv två ekvationer, en för varje möjlighet, och lös x för var och en av dem.

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 14

7. Lös problem med en eller noll lösningar. Två linjer som knappt berör varandra har en skärningspunkt, och två linjer som aldrig berör varandra har noll. Du kan känna igen dem på följande sätt:

En lösning: Problemen kan delas upp i två identiska faktorer ((x-1)(x-1) = 0). Inmatad i den kvadratiska formeln blir kvadratroten

\sqrt{0}

${sqrt{0}}$ . Du behöver bara lösa en ekvation.

Det finns ingen verklig lösning: Det finns inga faktorer som uppfyller kraven (notering till mellanperioden). Inmatad i kvadratformeln får du ett negativt tal under radikalen (t.ex

\sqrt{- 2}

${sqrt{-2}}$ ). Skriv "ingen lösning" som ditt svar.

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 15

8. Sätt tillbaka x-värdena i den ursprungliga ekvationen. När du har x-värdet för skärningspunkten, sätt tillbaka det i en av ekvationerna du började med. Lös för y för att hitta y-värdet. Om det finns ett andra x-värde, upprepa för detta värde också.

Exempel: Vi har hittat två lösningar,

X = 2

$x=2$ och

X = - 3

$x=-3$ . En av våra linjer har ekvationen

y = X + 7

$y=x+7$ . ersättning

y = 2 + 7

$y=2+7$ och

y = - 3 + 7

$y=-3+7$ , och lös varje ekvation så att du får

y = 9

$y=9$ och

y = 4

$y=4$ om du får svar.

Bild med titeln Hitta algebraiskt skärningspunkten mellan två linjer Steg 16

9. Skriv svaret som koordinater. Nu skriver du svaret som koordinater, med x-värdet och y-värdet för skärningspunkten. Om du har två svar, se till att du matchar rätt x-värde med varje y-värde.

Exempel: När vi

X = 2

$x=2$ input får vi

y = 9

$y=9$ , så att en skärningspunkt är lika med (2, 9). Vi gör samma sak för den andra lösningen, och detta ger oss skärningspunkten (-3, 4) på.

Tips

Ekvationer för en cirkel eller ellips har en $X 2$ $x^{2}$ termin och a $y 2$ $y^{2}$ termin. För att hitta skärningspunkten mellan en cirkel och en rät linje, lös x i den linjära ekvationen. Ersätt lösningen med x i cirkelekvationen, och andragradsekvationen blev mycket lättare. Dessa problem kan ha 0, 1 eller 2 lösningar, som redan indikerats i metoderna ovan.
En cirkel och en parabel (eller någon annan andragradsekvation) kan ha 0, 1, 2, 3 eller 4 lösningar. Hitta variabeln som är en kvadrat i båda ekvationerna — låt oss säga att detta är x. lösa $X 2$ $x^{2}$ på och ersätt svaret $X 2$ $x^{2}$ i den andra ekvationen. Lös y för att hitta 0, 1 eller 2 lösningarna. Koppla tillbaka varje lösning till den ursprungliga andragradsekvationen och lös x. Var och en av dessa kan ha 0, 1 eller 2 lösningar.