Om du gör ett misstag kan du enkelt upptäcka det genom att gå igenom alla dina tidigare steg. 
Exempel: ett objekt accelererar österut i 12 sekunder, med en hastighet av 10 m/s¬¬2 tills sluthastigheten på 200 m/s uppnås. Ge objektets initiala hastighet. Notera den kända informationen: Vi = ?, Vf = 200 m/s, a = 10 m/s, t = 12 s Multiplicera accelerationen och tiden. a x t = 10 x 12 = 120 Subtrahera produkten från sluthastigheten. Vi = Vf – (a x t) = 200 – 120 = 80 Vi = 80 m/s, öst. Skriv ditt svar i rätt form. Tänk på enheten, vanligtvis meter per sekund eller Fröken, samt objektets riktning (eftersom detta är vektorhastigheten). Utan riktningsinformation har du bara ett mått på hastighet, istället för vektorhastighet. 

Om du gör ett misstag är det lätt att upptäcka genom att gå igenom alla dina tidigare steg. 
Till exempel: Ett föremål accelererar i 30 sekunder med 7 m/s2 i västlig riktning över ett avstånd av 150 meter. Beräkna den initiala hastigheten för det objektet. Notera den kända informationen: Vi = ?, d = 150 m, a = 7 m/s, t = 30 s Multiplicera accelerationen med tiden. a x t = 7 *30 = 210 Dela produkten med två. (a x t) / 2 = 210 / 2 = 105 Dela avståndet efter tid. d/t = 150 / 30 = 5 Subtrahera den första fraktionen från den andra fraktionen. Vi = (d / t) - [(a x t) / 2] = 5 – 105 = -100 Vi = -100 m/s, västerut Skriv ditt svar i rätt form. Tänk på enheten, vanligtvis meter per sekund eller "m/s", samt objektets riktning (eftersom detta är vektorhastigheten). Utan riktningsinformation har du bara ett mått på hastighet, istället för vektorhastighet. 

Om du gör ett misstag är det lätt att upptäcka genom att gå igenom alla dina tidigare steg. 
Till exempel: Ett föremål som accelererar i nordlig riktning med 5 m/s2 över ett avstånd av 10 meter har en sluthastighet på 12 m/s. Beräkna objektets initiala hastighet. Notera den kända informationen: Vi = ?, Vf = 12 m/s, a = 5 m/s, d = 10 m Kvaddra sluthastigheten. Vf= 12 = 144 Multiplicera accelerationen med avståndet och multiplicera med två. 2 x a x d = 2 x 5 x 10 = 100 Subtrahera produkten av denna beräkning från föregående produkt. Vf - (2 x a x d) = 144 – 100 = 44 Beräkna kvadratroten av ditt svar. = √ [Vf - (2 x a x d)] = √44 = 6.633 Vi = 6.633 m/s, norrut. Skriv ditt svar i rätt form. Tänk på enheten, vanligtvis meter per sekund eller "m/s", samt objektets riktning (eftersom detta är vektorhastigheten). Utan riktningsinformation har du bara ett mått på hastighet, istället för vektorhastighet. 

Om du gör ett misstag kan du enkelt upptäcka det genom att gå igenom alla dina tidigare steg. 
Till exempel: Ett föremål har en sluthastighet på 3 m/s söderut och färdas en sträcka på 45 meter på 15 sekunder. Beräkna objektets initiala hastighet. Notera den kända informationen: Vi = ?, Vf = 3 m/s, t = 15 s, d = 45 m Dela avståndet efter tid. (d/t) = (45/15) = 3 Multiplicera värdet med två. 2 (d/t) = 2 (45/15) = 6 Subtrahera sluthastigheten från produkten. 2(d/t) - Vf = 6 - 3 = 3 Vi = 3 m/s, söderut. Skriv ditt svar i rätt form. Tänk på enheten, vanligtvis meter per sekund eller "m/s", samt objektets riktning (eftersom detta är vektorhastigheten). Utan riktningsinformation har du bara ett mått på hastighet, istället för vektorhastighet.
Bestäm initial hastighet
- Steg
- Metod 1 av 4: Bestämning av initialhastigheten med hjälp av sluthastighet, acceleration och tid
- Metod 2 av 4: Bestäm starthastigheten med avstånd, tid och acceleration
- Metod 3 av 4: Bestämning av initialhastigheten med hjälp av sluthastigheten, accelerationen och avståndet
- Metod 4 av 4: Bestämning av initialhastigheten med hjälp av sluthastigheten, tiden och avståndet
- Förnödenheter
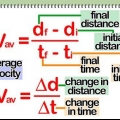
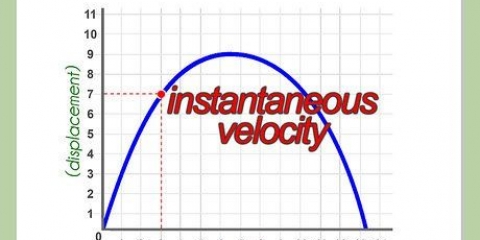
Vektorhastighet är en funktion av tiden och definieras av både en storlek och en riktning. Fysiska problem kräver ofta att du beräknar den initiala hastigheten (hastighet och riktning) med vilken ett visst föremål började röra sig. Det finns flera ekvationer som kan användas för att bestämma starthastigheten. Med informationen i ett problem kan du bestämma vilken ekvation du ska använda för att snabbt svara på frågan.
Steg
Metod 1 av 4: Bestämning av initialhastigheten med hjälp av sluthastighet, acceleration och tid

1. Känna till den korrekta ekvationen att använda. För att lösa alla fysikproblem måste du veta vilken formel du ska använda. Att skriva ner all känd information är det första steget för att hitta rätt ekvation. När du har hittat värdena för terminalhastighet, acceleration och tid kan du använda följande formel: Observera att denna ekvation är standardekvationen för att bestämma den initiala hastigheten.
- Initial hastighet: Vi = Vf - (a x t)
- Förstå innebörden av varje symbol.
- Vi står för "initial speed"
- Vf står för `sluthastighet`
- a står för "acceleration"
- t står för "tid"

2. Fyll i den kända informationen. När du har skrivit ner den kända informationen och bestämt den korrekta formeln kan du fylla i värdena för de korrekta variablerna. Det är mycket viktigt att ställa in varje problem noggrant och registrera varje steg i processen.

3. Lös ekvationen. När alla värden har angetts korrekt, använd rätt ordningsföljd för att lösa problemet. Använd en miniräknare om det tillåts för att undvika beräkningsfel.
Metod 2 av 4: Bestäm starthastigheten med avstånd, tid och acceleration

1. Känna till den korrekta ekvationen att använda. För att lösa alla fysikproblem måste du veta vilken formel du ska använda. Att skriva ner all känd information är det första steget för att hitta rätt ekvation. När du har hittat värdena för avstånd, acceleration och tid kan du använda följande formel:
- Initial hastighet: Vi = (d / t) - [(a x t) / 2]
- Förstå innebörden av varje symbol.
- Vi står för "initial speed"
- d står för "distans"
- a står för "acceleration"
- t står för "tid"

2. Fyll i den kända informationen. När du har skrivit ner den kända informationen och bestämt den korrekta formeln kan du fylla i värdena för de korrekta variablerna. Det är mycket viktigt att ställa in varje problem noggrant och registrera varje steg i processen.

3. Lös ekvationen. När alla värden har angetts korrekt, använd rätt ordningsföljd för att lösa problemet. Om du kan, använd en miniräknare för att undvika beräkningsfel.
Metod 3 av 4: Bestämning av initialhastigheten med hjälp av sluthastigheten, accelerationen och avståndet

1. Känna till den korrekta ekvationen att använda. För att lösa alla fysikproblem måste du veta vilken formel du ska använda. Att skriva ner all känd information är det första steget för att hitta rätt ekvation. När värdena för terminalhastighet, acceleration och avstånd är givna kan du använda följande formel:
- Initial hastighet: Vi = √ [Vf - (2 x a x d)]
- Förstå innebörden av varje symbol.
- Vi står för "initial speed"
- Vf står för `sluthastighet`
- a står för "acceleration"
- d står för "distans"

2. Fyll i den kända informationen. När du har skrivit ner den kända informationen och bestämt den korrekta formeln kan du fylla i värdena för de korrekta variablerna. Det är mycket viktigt att ställa in varje problem noggrant och registrera varje steg i processen.

3. Lös ekvationen. När alla värden har angetts korrekt, använd rätt ordningsföljd för att lösa problemet. Om du kan, använd en miniräknare för att undvika beräkningsfel.
Metod 4 av 4: Bestämning av initialhastigheten med hjälp av sluthastigheten, tiden och avståndet

1. Känna till den korrekta ekvationen att använda. För att lösa alla fysikproblem måste du veta vilken formel du ska använda. Att skriva ner all känd information är det första steget för att hitta rätt formel. Om värdena för terminalhastighet, avstånd och tid är kända kan du använda följande formel:
- Initial hastighet: Vi = 2(d/t) - Vf
- Förstå innebörden av varje symbol.
- Vi står för "initial speed"
- Vf står för `sluthastighet`
- t står för "tid"
- d står för "distans"

2. Fyll i den kända informationen. När du har skrivit ner den kända informationen och bestämt den korrekta formeln kan du fylla i värdena för de korrekta variablerna. Det är mycket viktigt att ställa in varje problem noggrant och registrera varje steg i processen.

3. Lös ekvationen. När alla värden har angetts korrekt, använd rätt ordningsföljd för att lösa problemet. Om du kan, använd en miniräknare för att undvika beräkningsfel.
Förnödenheter
- Penna
- Papper
- Miniräknare (valfritt)
"Bestäm initial hastighet"
Оцените, пожалуйста статью