Om draget tar dig till en "ruta" ovanför den magiska kvadraten, stanna kvar i den rutans kolumn, men placera numret i den nedre raden i den kolumnen. Om draget tar dig till en ruta till höger om den magiska kvadraten, stanna kvar på den raden, men placera numret i kolumnen på den raden, längst till vänster om kvadraten. Om flytten tar dig till en ruta som redan har ett nummer, gå tillbaka till föregående ruta som fylldes i och placera nästa nummer direkt ovanför den. 

summa = [6 * (62 + 1)] / 2 summa = [6 * (36 + 1)] / 2 summa = (6 * 37) / 2 summa = 222/2 Den magiska konstanten för en kvadrat på 6x6 är 222/2 eller 111. Alla rader, kolumner och diagonaler ska läggas ihop för att ge detta nummer. 
Så för varje 6x6 kvadrat blir varje kvadrant en 3x3 kvadrat. 
I exemplet med en 6x6 kvadrat löses kvadrant A med talen från 1-9; kvadrant B med de på 10-18; Kvadrant C med 19-27 och kvadrant D med 28-36. 
Behandla det första numret i varje kvadrant som om det vore ett. Placera den i den mittersta rutan på den översta raden i varje kvadrant. Behandla varje kvadrant som en liten magisk fyrkant. Även om rutan är tillgänglig i en intilliggande kvadrant, ignorera den och hoppa till "undantagsregeln" som passar denna situation. 
Använd en penna för att markera alla rutor i den översta raden tills du kommer till mittfältet i kvadrant A. Så i en 6x6 ruta markerar du ruta 1 (med siffran 8), men i en 10x10 ruta markerar du rutor 1 och 2 (med siffrorna 17 respektive 24). Markera en ruta med rutorna du just markerade som den översta raden. Om du bara har markerat en ruta kommer din ruta inte att bestå av mer än en ruta. Vi kallar detta Markering A-1. Så i en 10x10 magisk ruta består markör A-1 av rutor 1 och 2 på rad 1 och 2, vilket skapar en 2x2 ruta i den övre vänstra kvadranten. I raden omedelbart under Markör A-1, hoppa över siffran i den första kolumnen och markera sedan så många rutor från sida till sida som du angav i Markering A-1. Vi kallar denna mittrad Markering A-2. Urval A-3 är en ruta som liknar A-1, men placerad i det nedre vänstra hörnet av kvadranten. Val A-1, A-2 och A-3 bildar tillsammans markör A. Upprepa denna process i kvadrant D, skapa ett identiskt markörområde, markör D. 

Här är två bilder av en 14x14 Magic Square före och efter båda switcharna. Omkopplingsytan för kvadrant A är markerad i blått, ytan för kvadrant D är grön, för kvadrant C gul och för kvadrant B orange. Magic Square på 14x14 före växlingen (steg 6, 7 och 8) Magic Square på 14x14 efter att ha utfört bytena (steg 6, 7 och 8) 

summa = [4 * (42 + 1)] / 2 summa = [4 * (16 + 1)] / 2 summa = (4 * 17) / 2 summa = 68/2 Den magiska konstanten för en kvadrat på 4x4 är 68/2 eller 34. Alla rader, kolumner och diagonaler måste bilda detta nummer. 
Markera bara de fyra hörnrutorna i en 4x4 ruta. I en 8x8-ruta är varje markör ett 2x2-område i hörnen. I en 12x12 ruta är varje markör ett område på 3x3 i hörnen osv. 
I en kvadrat på 4x4 är den centrala markören ett område på 2x2 i mitten. I en kvadrat på 8x8 är den centrala markören ett område på 4x4 i mitten osv. 
1 i den övre vänstra rutan och 4 i den övre högra rutan 6 och 7 i mittrutorna på rad 2 10 och 11 i mittrutorna på rad 3 13 i den nedre vänstra rutan och 16 i den nedre högra rutan. 
15 och 14 i mittrutorna på rad 1 12 i rutan längst till vänster och 9 i rutan längst till höger på rad 2 8 i rutan längst till vänster och 5 i rutan längst till höger på rad 3 3 och 2 i mittrutorna på rad 4 Vid denna tidpunkt bör alla kolumner, rader och diagonaler ha en summa som är lika med den tidigare beräknade magiska konstanten.
Lös magiska rutor
Magiska rutor har bara vuxit i popularitet sedan uppkomsten av matematikbaserade spel som Sudoku. En magisk kvadrat är ett arrangemang av tal i en kvadrat på ett sådant sätt att summan av varje rad, kolumn och diagonal är ett konstant tal, den så kallade magiska konstanten. Den här artikeln kommer att förklara hur man löser alla slags magiska rutor, vare sig det är en udda, enkel jämn eller dubbel jämn ruta.
Steg
Metod 1 av 3: Lösa en udda magisk ruta

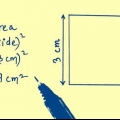
1. Beräkna den magiska konstanten. Du kan hitta detta tal med en enkel matematisk formel, där n = antalet rader eller kolumner i din magiska kvadrat. Så, till exempel, i en 3x3 magisk kvadrat, n = 3. Den magiska konstanten = [n * (n2 + 1)] / 2. Så i exemplet med kvadraten 3x3:
- summa = [3 * (32 + 1)] / 2
- summa = [3 * (9 + 1)] / 2
- summa = (3 * 10) / 2
- summa = 30/2
- Den magiska konstanten för en 3x3 kvadrat är 30/2 eller 15.
- Alla rader, kolumner och diagonaler har detta nummer som summa.

2. Placera nummer 1 i den mittersta rutan på den översta raden. Det här är alltid punkten där du börjar om din magiska kvadrat med sidor har ett udda antal sidor, oavsett hur stort eller litet talet är. Så om du har en kvadrat på 3x3, lägg siffran 1 i ruta 2; i en ruta på 15x15, placera siffran 1 i ruta 8.

3. Fyll i de återstående siffrorna i ett mönster från en till höger. Du fyller alltid i siffrorna enligt en serie (1, 2, 3, 4 osv.) genom att gå upp en rad och sedan en kolumn till höger. Du märker direkt att för att placera siffran 2 hamnar du ovanför den översta raden, utanför den magiska fyrkanten. Det är okej - även om du alltid använder en-upp, en-till-höger-metoden, finns det tre undantag som också följer ett förutsägbart mönster:
Metod 2 av 3: Lösa en enkel jämn magisk ruta

1. Förstå vad en enkel jämn kvadrat är. Alla vet att ett jämnt tal är delbart med 2, men med magiska rutor finns det olika metoder för att lösa enkla och dubbla jämna rutor.
- En enkel jämn kvadrat har ett antal rutor per sida som är delbart med 2, men inte med 4.
- Den minsta enstaka magiska kvadraten är 6x6, eftersom 2x2 magiska rutor inte kan skapas.

2. Beräkna den magiska konstanten. Använd samma metod som för udda magiska rutor: den magiska konstanten = [n * (n2 + 1)] / 2, där n = antalet rutor per sida. Så, i exemplet med en 6x6 kvadrat:

3. Dela den magiska fyrkanten i fyra lika stora kvadranter . Märk dem A (överst till vänster), C (överst till höger), D (nedre till vänster) och B (nederst till höger). För att bestämma hur stor varje ruta ska vara, dela antalet rutor i varje rad eller kolumn på mitten.

4. Tilldela ett antal nummer till varje kvadrant. Kvadrant A får en fjärdedel av siffrorna; kvadrant B andra kvartalet; Kvadrant C det tredje kvartalet och kvadrant D det sista kvartalet av det totala nummerområdet för en 6x6 magisk ruta.

5. Lös varje kvadrant med den magiska kvadratmetoden med ett udda antal rutor per sida. Kvadrant A är lätt att fylla i eftersom den börjar med siffran 1, som magiska rutor brukar göra. Kvadranter B-D börjar dock med udda tal — 10, 19 och 28, som i vårt exempel.

6. Gör markörerna A och D. Om du har försökt lägga till kolumner, rader och diagonaler direkt, har du märkt att de inte går ihop med den magiska konstanten. Du kommer att behöva byta några rutor i de övre vänstra och nedre vänstra kvadranten för att fullborda din magiska ruta. Vi kallar dessa områden för Markör A och Markör D.

7. Byt markörer A och D. Detta är ett 1-till-1 utbyte. Flytta rutorna mellan kvadrant A och kvadrant D utan att ändra ordningen. När du har gjort detta ska alla rader, kolumner och diagonaler i din magiska kvadrat ha den tidigare beräknade magiska konstanten som summa.

8. Byt en extra gång mot individuella till och med magiska kvadrater större än 6x6. Utöver växlingen för kvadranter A och D som nämns ovan, måste du också göra en växling för kvadranter C och B. Markera kolumnerna från höger sida av kvadraten till vänster, en mindre än antalet kolumner markerade för markering A-1. Byt ut värdena i kvadrant C med värdena i kvadrant B för dessa kolumner, med samma en-till-en-metod.
Metod 3 av 3: Lösa en dubbel jämn magisk ruta

1. Förstå vad en dubbel jämn kvadrat är. En enkel jämn kvadrat har ett antal rutor per sida som är delbart med 2. En dubbel jämn ruta har ett antal rutor per sida som är delbara med 4.
- Den minsta dubbelt jämna kvadraten som kan göras är 4x4 kvadraten.

2. Beräkna den magiska konstanten. Använd samma metod som för de udda eller singulära jämna magiska kvadraterna: den magiska konstanten = [n * (n2 + 1)] / 2, där n = antalet rutor per sida. Så, i exemplet med en 4x4 kvadrat:

3. Applicera markörer A-D. I varje hörn av den magiska kvadraten, placera en liten kvadrat med sidorna n/4, där n = längden på en sida av hela den magiska kvadraten. Märk dem moturs som markeringar A, B, C och D.

4. Placera det centrala märket. Markera alla rutor i mitten av den magiska kvadraten i ett kvadratiskt område med längden n/2, där n = längden på varje sida av en komplett magisk kvadrat. Den centrala markören får inte överlappa markörerna A-D, utan ska vidröra dem i hörnen.

5. Fyll i den magiska rutan, men bara i de markerade områdena. Börja fylla i dina magiska rutor från vänster till höger, men placera bara ett nummer om rutan faller inom en markör. Så, i en 4x4-låda, fyll i följande rutor:

6. Fyll i resten av den magiska kvadraten genom att räkna bakåt. Detta är i huvudsak motsatsen till föregående steg. Börja igen med den övre vänstra rutan, men hoppa över alla rutor som hamnar i det markerade området, och fyll i de omarkerade rutorna genom att räkna bakåt. Börja med det största numret i ditt nummerområde. Så, i en 4x4 magisk ruta, fyll i:
Tips
- Prova varianter av dessa steg för att upptäcka dina egna lösningsmetoder.
Förnödenheter
- Penna
- Papper
- Suddgummi
Оцените, пожалуйста статью