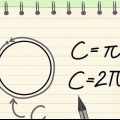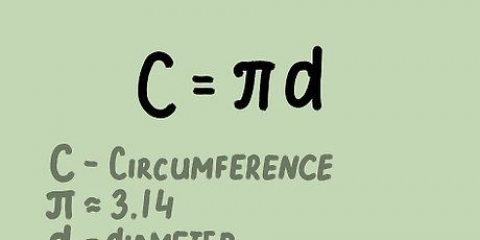Om kvadraten har en sida med längden 4:Omkrets = 4 * 4, med andra ord 16. Om kvadraten har en sida med längden 6: Omkrets = 4 * 6, med andra ord 24. 

Om arean på kvadraten är 20, är sidans längd s: =√20 eller 4.472 Om arean på kvadraten är 25, är sidans längd s = √25 eller 5. 
För en kvadrat med en area på 20 och en sidolängd på 4,473 är omkretsen: Omkrets = 4 * 4,472 eller 17 888. För en kvadrat med en area på 25 och en sidolängd på 5 är omkretsen: Omkrets = 4 * 5 eller 20. 


a + a = (2r), nu kan vi förenkla: 2a = 4(r), dividera nu båda sidor med 2: (a) = 2(r), ta nu kvadratroten av varje sida: a = √(2)r.Vår längd på en sida s av den inskrivna kvadraten = √(2)r. 

Notera: du kunde också ha gjort det så här: multiplicera radien (10) med talet 5 567. 10*5.567 = 56.57, men eftersom det kan vara svårt att komma ihåg, bör du gå igenom hela processen.
Beräkna omkretsen av en kvadrat
Omkretsen av en tvådimensionell figur är det totala avståndet runt figuren, eller summan av längderna på sidorna. Definitionen av en kvadrat är en figur med fyra lika sidor och fyra räta vinklar (90°) mellan dessa sidor. Eftersom alla sidor har samma längd är det mycket lätt att bestämma omkretsen av en kvadrat! Den här artikeln tar först upp hur man beräknar omkretsen av en kvadrat om du vet längden på en av dess sidor. Sedan visar vi dig hur du beräknar omkretsen om du bara känner till arean, och i det sista avsnittet kommer vi att lära dig hur du beräknar omkretsen av en inskriven kvadrat i en cirkel vars radie är känd.
Steg
Metod 1 av 3: Hitta omkretsen av en kvadrat om du vet längden på en sida

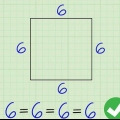
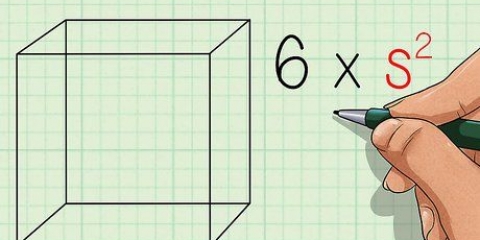
1. Tänk på formeln för omkretsen av en kvadrat. För en kvadrat där vi hittar längden på sidan s omkretsen är helt enkelt fyra gånger längden på den sidan: Omkrets = 4s (observera: i bilderna används bokstaven P för kontur, från den engelska `perimeter`).

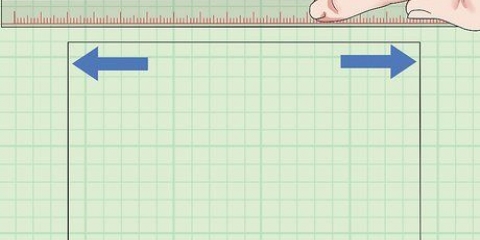
2. Hitta längden på en sida och multiplicera den med 4 för att hitta omkretsen. Beroende på uppdraget kan du behöva mäta med en linjal eller titta på annan information för att bestämma längden på en sida. Här är några exempel på omkretsberäkningar:
Metod 2 av 3: Bestäm omkretsen av en kvadrat om du känner till dess area

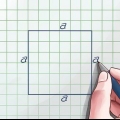
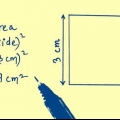
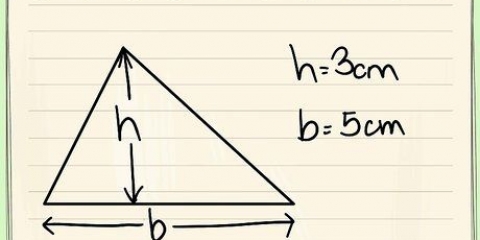
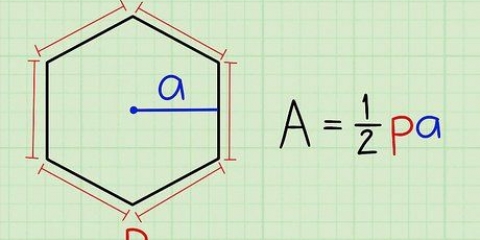
1. Känna till formeln för arean av en kvadrat. Arean av vilken rektangel som helst (kom ihåg att rutor är speciella rektanglar) kan definieras som bas gånger höjd.Eftersom bas och höjd är lika i fallet med en kvadrat, är arean av en kvadrat med sida s: s*s. Med andra ord: area = s.

2. Ta kvadratroten av området. Kvadratroten av området ger dig längden på en av kvadratens sidor. För de flesta siffror behöver du en miniräknare för att beräkna kvadratroten. Skriv in numret först och tryck sedan på kvadratroten (√).

3. Multiplicera längden på sidan med 4 för att hitta omkretsen. Använd sidlängdsvärdet du just hittade i formeln Omkrets = 4s. Resultatet är omkretsen av din kvadrat!
Metod 3 av 3: Beräkna omkretsen av en inskriven kvadrat i en cirkel om du känner till radien

1. Förstå vad en inskriven kvadrat är. En inskriven kvadrat i en cirkel är en fyrkant som ritas i en cirkel med alla hörn av kvadraten vidrör cirkeln.

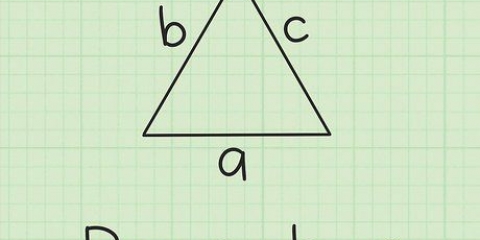
2. Förstå förhållandet mellan cirkelns radie och längden på kvadratens sidor. Avståndet från mitten av en inskriven kvadrat till ett hörn är lika med cirkelns radie. Till sidans längd s för att hitta måste vi först föreställa oss att vi halverar kvadraten diagonalt, så att två liksidiga trianglar bildas. Dessa trianglar har lika sidor a och b och en hypotenusa c, som vi vet är lika med två gånger cirkelns radie, dvs 2r.

3. Använd Pythagoras sats för att hitta längden på sidan av kvadraten. Pythagoras sats är som följer: i en rätvinklig triangel är summan av kvadraterna av längderna på de rektangulära sidorna (a,b) lika med kvadraten på hypotenusans längd (c), a + b = c. Eftersom sidor a och b är lika (vi har fortfarande att göra med en kvadrat!) och det vet vi c=2r vi kan nu skriva ut ekvationen och förenkla den för att hitta längden på en sida:

4. Multiplicera längden på en sida av kvadraten med fyra för att hitta omkretsen. I det här fallet är kvadratens omkrets: Omkrets = 4√(2)r. Omkretsen av en inskriven kvadrat i en cirkel är därför alltid lika med 4√(2)r, eller ungefär 5,657r

5. Lös en exempelfråga. Vi tar en inskriven kvadrat i en cirkel med en radie på 10. Det betyder att kvadratens diagonal = 2(10) eller 20. Pythagoras sats lär oss att: 2(a) = 20, Så 2a = 400. Dela nu båda sidor med två, det ser vi a = 200. Ta kvadratroten av varje sida och vi ser det a = 14,142. Multiplicera detta med 4 för att hitta omkretsen av din kvadrat: Omkrets = 56,57.
Оцените, пожалуйста статью