2 x 2 x 3 x 5 x 7 = 420.
LCF för 20 och 42 är 420.


8 x 1 = 8
8 x 2 = 16
8 x 3 = 24 
LCF för 5 och 8 är 40. Detta är den minsta gemensamma multipeln eftersom det är en först förekommande faktor av samma multipel för både 5 och 8, och därmed LCF för dessa tal.



18/2 = 9, så skriv 9 under 18. 12/2 = 6, så skriv 6 under 12. 30/2 = 15, så skriv 15 under 30. 
Faktor 3 av dessa siffror. 3 är den minsta primtalsfaktorn här, det minsta primtal är delbart med båda talen.
Dividera alla tre siffrorna med 3 och skriv resultatet under dessa siffror.
9/3 = 3, så du skriver en 3 under 9; 6/3 = 2, så du skriver en 2 under 6; 15/3 = 5 så du skriver en 5 under 15.

Anta som ett exempel att de nedersta talen är 2, 39 och 122, dividera sedan 2 och 122 med 2, vilket resulterar i en ny nedre rad: 1, 39 och 61. 
LCF för 18, 12 och 30 är 180.

Dela sedan det andra talet (45) med resten (30). 45/30 = 1 (resten 15). Så 45 = 1 x 30 + 15.
Dela sedan resten från det första steget (30) med resten från det andra steget (15). 30/15 = 2 (resterande 0). Så 30 = 2 x 15 + 0.
GGD på 210 och 45 är 15.
Du kan alltid använda den här metoden för att hitta GGD – sluta bara dela när du når en återstod på 0. 


Hitta den minsta gemensamma multipeln av två tal
Den minsta gemensamma multipeln (KGB) av en grupp av tal är det minsta talet som är en multipel av alla tal i gruppen. Till exempel är LCF för 16 och 20 80; 80 är det minsta talet som är både en multipel av 16 och en multipel av 20. Du kan hitta LCF för två eller flera nummer med olika metoder. Om du vill veta hur du hittar LCF för två eller flera nummer, följ dessa steg.
Steg
Metod 1 av 4: Primfaktorisering

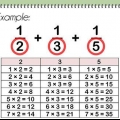
1. Bestäm primtalsfaktorerna för båda talen. Detta är en idealisk metod för större antal. Det första steget för att hitta den minsta gemensamma multipeln av två tal med den här metoden är faktoriseringen av båda talen till primtalen multiplicerade för att få det talet som en produkt. Du kan börja med att göra en lista med två tal (faktorer) multiplicerade med varandra för att producera det talet och sedan faktorisera dem i deras primtalsfaktorer. Anta att du vill hitta den minsta gemensamma multipeln av 20 och 42. Så här faktoriseras det. 20 = 2 x 2 x 542 = 2 x 3 x 7

2. Skriv ner vilket primtal som förekommer oftast i primtalsfaktorerna för varje tal. Här är en lista över tal som förekommer oftast för varje primtal i föregående exempel 2 → 2 gånger3 → 1 gång5 → 1 gång7 → 1 gång
3. Multiplicera alla faktorer tillsammans . Så här behöver du göra för att hitta exemplets EKG:


Metod 2 av 4: Lista alla multiplar av båda talen

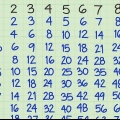
1. Lista några multiplar av det första talet i stigande ordning. Detta är en idealisk metod för mindre tal, särskilt för nummer mindre än 10. För större antal rekommenderas detta inte eftersom det kan bli svårt. Anta att du vill hitta KGV för 5 och8. Du gör först en lista över multiplerna av 55 x 1 = 55 x 2 = 105 x 3 = 15

2. Lista nu några multiplar av det andra talet (8), i stigande ordning.
8 x 2 = 16
8 x 3 = 24

3. Prova ett antal möjligheter för båda talen tills du har hittat den minsta gemensamma multipeln. I vissa fall kan du hitta LCF efter några försök för varje nummer. Fortsätt i det här exemplet tills du hittar en minsta gemensamma multipel för 5 och 8. Det är din kgf
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
8 x 4 = 32
8 x 5 = 40
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
8 x 4 = 32
8 x 5 = 40

Metod 3 av 4: Använd en gemensam multipeltabell

1. Skriv siffrorna överst i en tabell med gemensamma multiplar. Lämna lite utrymme på vänster sida av siffrorna, och så mycket utrymme som möjligt under siffrorna. Anta att vi har siffrorna 18, 12 och 30. Skriv varje nummer i sin egen kolumn, högst upp i tabellen.

2. Skriv den minst vanliga primfaktorn av talen i utrymmet till vänster. Leta efter den minsta primtalsfaktorn (som 2, 3 eller 5) som du kan räkna ut av alla tal. De är alla jämna tal, så minst 2 är möjliga.

3. Dividera vart och ett av de tal du antar med den gemensamma primtalsfaktorn. Skriv kvoten under varje nummer. Så här kommer det att se ut:

4. Upprepa processen att faktorisera och dividera med den lägsta primfaktorn tills det inte finns några faktorer kvar. Upprepa för siffrorna 9, 6 och 15.




5. Om två av talen fortfarande delar en gemensam primtalsfaktor, fortsätt denna procedur tills inget av de nedersta talen har en gemensam faktor. När det gäller detta exempel är du nu klar.

6. Multiplicera alla siffror i den första kolumnen med de vanliga primtalsfaktorerna, med talen längst ner i alla andra kolumner. Det här är KGV. I det här exemplet är produkten av kolumnen gemensamma faktorer lika med 6 (2 x 3). Multiplicera 6 med siffrorna längst ner i de andra kolumnerna: 6 x 3 x 2 x 5 = 180.

Metod 4 av 4: Euklids algoritm
1. Använd Euklids algoritm för att hitta den största gemensamma divisorn (GGD) av två tal. Antag att de två talen i ett exempel210 och 45 är. Här är ett exempel på hur man använder Euklids algoritm för att hitta GGD för båda talen:
- Dividera det första talet med det andra: 210/45 = 4 (rest 30). Det betyder att 210 = 4 x 45 + 30.





2. Multiplicera de två ursprungliga talen. 210 x 45 = 9 450

3. Dividera resultatet med GGD för båda talen. 9 450/15 = 630. 630 är LCF på 210 och 45.

4. Använd Euklids algoritm för att hitta LCF för tre tal. För att göra detta, sök helt enkelt efter GCD för två siffror och använd sedan den GGD för att hitta VCF för dessa två siffror och det tredje numret.
Tips
- Om du vill veta om VCF är mindre eller större än produkten, använd den här metoden: om GGD är 1, så är VCF produkten. Om GGD är större än 1 kommer VCGV att vara mindre än produkten.
- KGV har många tillämpningar. Det vanligaste är att när du adderar eller subtraherar bråk så måste de ha samma nämnare; om så inte är fallet måste du göra dem eponyma, så att de har samma nämnare. Det bästa sättet att göra detta är att leta efter den minsta gemensamma nämnaren – som helt enkelt är densamma som nämnarnas LCF. Till exempel, för att beräkna 1/6 + 3/8, låt oss hitta LCF för 6 och 8, vilket är 24, och sedan konvertera varje bråktal så att båda nämnarna är lika med 24, och lämnar summan som ser ut så här: 4/24 + 24/9. Vi kan nu helt enkelt beräkna detta genom att addera täljaren tillsammans med svaret: 13/24.
- Om du behöver hitta LCF för fler än 2 nummer måste din metod ovan ändras något eftersom den bara fungerar för 2 nummer samtidigt. För att till exempel hitta LCF för 16, 20 och 32 börjar vi med att hitta LCF för 16 och 20 (vilket är lika med 80) och sedan LCF för 80 och 32, som kommer ut till 160.
- Till exempel, för att hitta CHF på 16 och 20, tar vi GGD på 16 och 20, som kommer ut till 4. 16 × 20 = 320 och 320 ÷ 4 = 80, så 80 är KGV.
- Om du vill göra en bråkdel av samma namn måste du veta hur många gånger varje nämnare går i LCF. Med den här metoden kan du hitta omvandlingsfaktorn genom att multiplicera alla siffror längst ner i alla andra kolumner (förutom den första där alla primtalsfaktorer är listade). Så för att konvertera 18 till 180, multiplicera det med 2 och 5. För att konvertera 12 till 180, multiplicera det med 3 och 5.För att konvertera 30 till 180, multiplicera det med 3 och 2.
Förnödenheter
- Penna.
- Suddgummi.
- Miniräknare (valfritt).
"Hitta den minsta gemensamma multipeln av två tal"
Оцените, пожалуйста статью