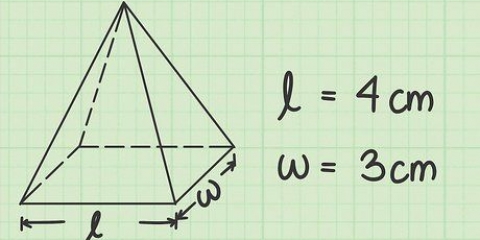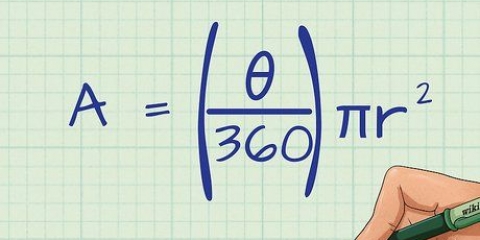Anteckna denna mätning som a. Exempel: a = 2 cm 
Observera att detta steg beräknar arean av en yta på kuben. Exempel: a = 2 cm a = 2 x 2 = 4 cm 
Detta steg avslutar beräkningen av kubens yta. Exempel: a = 4 cm Yta = 6 x a = 6 x 4 = 24 cm 

Mät längden på basen för att bestämma prismats längd och tilldela den till c. Exempel: c = 5 cm Mät bredden på basen för att bestämma prismats bredd och kalla det a. Exempel: a = 2 cm Mät höjden på sidan för att bestämma prismats höjd och kalla det b. Exempel: b = 3 cm 
Exempel: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Exempel: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Exempel: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Exempel: Area = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

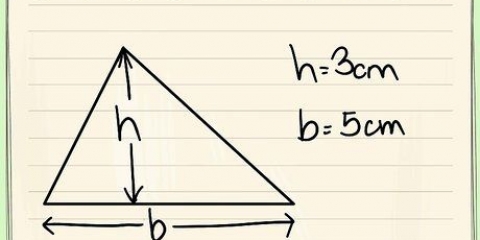
Basen b, är lika med längden på triangelns botten. Exempel: b = 4 cm Höjden h av den triangulära basen är lika med avståndet mellan den nedre kanten och spetsen. Exempel: h = 3 cm Arean av en triangel multiplicerat med 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Exempel: H = 5 cm De tre sidorna hänvisar till de tre sidorna av den triangulära basen. Exempel: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Exempel: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Exempel: P x H = 12 x 5 = 60 cm 
Exempel: 2A + PH = 12 + 60 = 72 cm. 

Exempel: r = 3 cm 
Exempel: r = r x r = 3 x 3 = 9 cm 
Exempel: π*r = 3,14 x 9 = 28,26 cm 
Exempel: 4π*r = 4 x 28,26 = 113,04 cm 

Exempel: r = 3 cm Exempel: h = 5 cm 
Exempel: Arean av basen = π*r = 3,14 x 3 x 3 = 28,26 cm Exempel: 2π*r = 2 x 28,26 = 56,52 cm 
Exempel: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm 
Exempel: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm 

Exempel: l = 3 cm Exempel: s = 1 cm 
Exempel: s = s x s = 1 x 1 = 1 cm 
Exempel: 2 x s x l = 2 x 1 x 3 = 6 cm 
Exempel: s + 2 lm = 1 + 6 = 7 cm 

Exempel: r = 2 cm Exempel: h = 4 cm 
Exempel: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm 
Exempel: π*r = 3,14 x 2 x 2 = 12,56 cm 
Exempel: π*rl = 3,14 x 2 x 4,47 = 28,07 cm 
Exempel: π*r + π*rl = 12,56 + 28,07 = 40,63 cm
Beräkna area
Area är det totala utrymmet som upptas av alla områden av ett objekt. Det är summan av alla områden av det objektet. Att bestämma arean för en tredimensionell form är ganska lätt, så länge du använder rätt formel. Varje form har sin egen separata formel, så du måste först kontrollera vilken form det är. Att beräkna areaformeln för olika objekt kan göra beräkningarna enklare i framtiden. Här diskuterar vi några av de vanligaste formerna du kan stöta på.
Steg
Metod 1 av 7: Kub

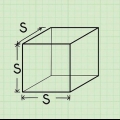
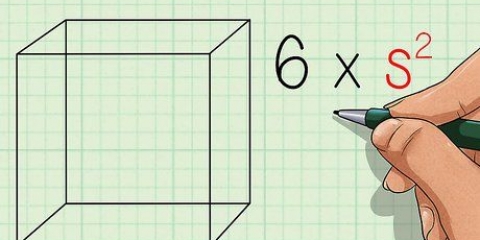
1. Definiera formeln för arean av en kub. En kub har sex identiska ytor. Eftersom både längden och bredden på en kvadrat är lika, är arean på en kvadrat a, varigenom a längden är en sida. Eftersom en kub har sex lika stora ytor, kan du beräkna dess area genom att multiplicera arean av ett av dess ytor med sex. Formeln för arean av en kub O är O = 6a, varigenom a längden är en sida.
- Ytenheterna är en viss längd i kvadrat: cm, dm, m, etc.

2. Mät längden på ena sidan. Per definition bör varje sida eller kant (kant) av en kub vara lika med den andra, så du behöver bara mäta en sida. Mät längden på sidan med en linjal. Var uppmärksam på de enheter du använder.

3. Kvadra ditt mått för a. Kvadra måttet för att beräkna längden på revbenet. Att kvadrera ett värde innebär att multiplicera det med sig självt. Om du lär dig detta för första gången kan det vara bra att komma ihåg detta som NT= 6*a*a.

4. Multiplicera denna produkt med sex. Kom ihåg att en kub har sex identiska ytor. Nu när du känner till arean av ett av ansiktena, multiplicera det med sex (på grund av alla sex ansikten).
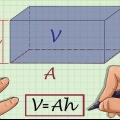
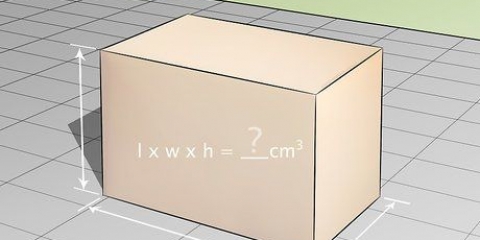
Metod 2 av 7: Rektangulärt prisma

1. Definiera formeln för arean av ett rektangulärt prisma. Liksom en kub har ett rektangulärt prisma sex ytor, men till skillnad från en kub är dessa ytor inte lika. I ett rektangulärt prisma är endast de motsatta ytorna lika med varandra. Därför, när man beräknar arean av ett rektangulärt prisma, måste de olika längderna på revbenen beaktas, som i formeln SA = 2ab + 2bc + 2ac.
- För denna formel, a lika med prismats bredd, b lika med höjden och c lika med längden.
- Om vi tittar närmare på formeln ser du att vi helt enkelt lägger ihop alla områden på varje yta av objektet.
- Ytenheten kommer att vara en viss längd i kvadrat: cm, dm, m, etc.

2. Mät längden, höjden och bredden på varje sida. Alla tre avläsningarna kan vara olika, så var och en måste mätas separat. Mät varje sida med en linjal och registrera värdet. Använd samma enheter för varje mätning.

3. Beräkna arean av en av prismats ytor och multiplicera den med två. Kom ihåg att det finns sex ytor i ett rektangulärt prisma, och att de motsatta ytorna är lika med varandra. Multiplicera längden och höjden, eller c och a, för att hitta arean på ett plan. Ta detta mått och multiplicera det med två för att ta hänsyn till det motsatta identiska planet.

4. Hitta arean av prismats andra yta och multiplicera det med två. Som med den första uppsättningen ansikten, multiplicera bredden och höjden, eller a och b för att bestämma arean av en annan yta av prismat. Multiplicera detta mått med två för att ta hänsyn till de motsatta identiska sidorna.

5. Beräkna arean av prismats ändar och multiplicera det med två. Prismats andra två ytor är ändarna. Multiplicera längden och bredden (c och b) för att hitta deras yta. Multiplicera detta område med två för att ta hänsyn till båda sidor.

6. Lägg ihop de tre separata områdena. Eftersom arean av prismat är den totala arean av alla ytor på ett objekt, är det sista steget att lägga ihop alla individuellt beräknade ytor. Lägg till områdena på alla sidor tillsammans för att få den totala ytan.
Metod 3 av 7: Triangulärt prisma

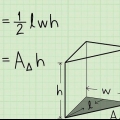
1. Definiera areaformeln för ett triangulärt prisma. Ett triangulärt prisma har två identiska triangulära ytor och tre rektangulära ytor. För att hitta arean måste du beräkna arean av alla ansikten och lägga ihop dem. Arean av ett triangulärt prisma är SA = 2A + PH, där A är arean av den triangulära basen, P är omkretsen av den triangulära basen och h är prismats höjd.
- För den här formeln håller det a de arean av en triangel och sålunda A = 1/2 bh, varigenom b är basen av triangeln och h höjden.
- sid är omkretsen av triangeln beräknad genom att addera alla tre kanterna på triangeln.
- Ytenheterna är en längdenhet i kvadrat: cm, dm, m, etc.

2. Beräkna arean av det triangulära planet och multiplicera det med två. Arean av en triangel är /2b*h där b är basen av triangeln och h är höjden. Så eftersom det finns två identiska trianglar som ansikten multiplicerar vi formeln med två. Detta gör beräkningen för båda planen enkel (b*h).

3. Mät varje sida av triangeln och prismats höjd. För att slutföra areaberäkningen måste du veta längden på varje sida av triangeln och höjden på prismat. Höjden är avståndet mellan de två triangulära ytorna.

4. Hitta omkretsen av triangeln. Omkretsen av triangeln kan beräknas genom att addera alla uppmätta sidor tillsammans: S1 + S2 + S3.

5. Multiplicera basens omkrets med prismats höjd. Kom ihåg att prismats höjd är avståndet mellan de två triangulära ytorna. Med andra ord, multiplicera sid av va.

6. Lägg till de två separata avläsningarna tillsammans. Du måste lägga till de två måtten från de föregående två stegen tillsammans för att få arean av det triangulära prismat.
Metod 4 av 7: Bol

1. Definiera areaformeln för en sfär. En sfär har en krökt yta, så ytarean är ett värde multiplicerat med konstanten pi. Arean av en sfär beräknas med hjälp av ekvationen NT = 4π*r.
- För denna formel, r lika med sfärens radie. Pi (eller π) kan avrundas till 3,14.
- Enheterna för området kommer att vara en längdenhet, i kvadrat: cm, dm, m, etc.

2.Mät radien av glödlampan. Sfärens radie är halva diametern, eller avståndet från sfärens centrum till kanten.

3. Kvadra radien. För att kvadrera ett tal, multiplicera det med sig självt. Multiplicera måttet för r med sig själv. Kom ihåg att denna formel kan skrivas om till SA = 4π*r*r.

4. Multiplicera den kvadratiska radien med en avrundning av pi. Pi är en konstant som representerar förhållandet mellan en cirkels omkrets och dess diameter. Det är ett irrationellt tal med många siffror efter decimalkomma. Det avrundas ofta till 3,14. Multiplicera den kvadratiska radien med π, eller 3,14, för arean av ett cirkulärt tvärsnitt av sfären.

5. Multiplicera denna produkt med fyra. För att slutföra beräkningen, multiplicera den med fyra. Hitta sfärens area genom att multiplicera den platta cirkulära arean med fyra.
Metod 5 av 7: Cylinder

1. Definiera areaformeln för en cylinder. En cylinder har två cirkulära ändar som stänger en rörformig yta. Formeln för arean av en cylinder är NT = 2π*r + 2π*rh, varigenom r är lika med radien för den cirkulära basen och h är lika med cylinderns höjd. runda pi (eller π) minskar till 3,14.
- Formeln 2π*r beräknar arean av de två cirkulära ändarna, medan 2πrh är arean av kolumnen mellan de två ändarna.
- Ytenheterna är en längdenhet i kvadrat: cm, dm, m, etc.

2. Mät cylinderns radie och höjd. En cirkels radie är halva dess diameter, eller avståndet från cirkelns centrum till kanten. Höjden är cylinderns totala avstånd från ena änden till den andra. Rita dessa mått med en linjal och skriv ner dem.

3. Hitta arean av basen och multiplicera den med två. För att hitta arean av basen, använd areaformeln eller en cirkel (π*r). För att slutföra beräkningen, kvadrera radien och multiplicera den med pi. Multiplicera sedan med två på grund av den andra identiska cirkeln i andra änden av cylindern.

4. Beräkna själva cylinderns yta med 2π*rh. Detta är formeln för att beräkna arean av ett rör. Röret är utrymmet mellan cylinderns två cirkulära ändar. Multiplicera radien med två, pi och höjden.

5. Lägg till de två separata avläsningarna tillsammans. Lägg till arean av de två cirklarna till arean av utrymmet mellan de två cirklarna för att beräkna cylinderns totala area. Obs: När du lägger till dessa två delar känner du igen den ursprungliga formeln: NT =2π*r + 2π*rh.
Metod 6 av 7: Square Pyramid

1. Definiera areaformeln för en kvadratisk pyramid. En fyrkantig pyramid har en kvadratisk bas och fyra triangulära sidor. Som nämnts är arean av en kvadrat längden på en sida i kvadrat. Arean av en triangel är 1/2sl (triangelns sida gånger triangelns längd eller höjd). Eftersom det finns fyra trianglar, beräknar du den totala arean genom att multiplicera det med fyra. Att lägga till alla dessa ytor tillsammans ger ekvationen för arean för en fyrkantig pyramid: NT = s + 2 kanal.
- I denna ekvation, s längden på varje sida av den kvadratiska basen och l lutningshöjden på varje triangulär sida.
- Ytenheten är en viss längdenhet i kvadrat: cm, dm, m, etc.

2. Mät den lutande höjden och bassidan. Den sneda höjden l, är höjden på en av de triangulära sidorna. Det är avståndet från basen till spetsen av pyramiden, mätt längs en platt sida. Den grundläggande sidan s, är längden på en sida av den kvadratiska basen. Eftersom basen är kvadratisk är detta mått lika för alla sidor. Använd en linjal för varje mått.

3. Hitta arean av den kvadratiska basen. Arean av en kvadratisk bas kan beräknas genom att kvadrera längden på en sida (s multiplicera med sig själv).

4. Beräkna den totala arean av de fyra triangulära ytorna. Den andra delen av ekvationen är arean av de återstående fyra triangulära ytorna. Med formeln 2ls multiplicerar vi s av l och två. Hitta området för varje ansikte.

5. Lägg till de två separata områdena tillsammans. Lägg till den totala arean av ytorna till arean av basen för att beräkna den totala arean.
Metod 7 av 7: Kon

1. Definiera areaformeln för en kon. En kon har en cirkulär bas och en rund yta som avsmalnar vid en punkt. För att hitta arean, ta arean av den cirkulära basen och arean av konen och addera de två tillsammans. Formeln för arean av en kon är: SA = π*r + π*rl, varigenom r radien är från den cirkulära basen, l konens sneda höjd och π är konstanten pi (3.14).
- Ytenheten är en viss längdenhet i kvadrat: cm, dm, m, etc.

2. Mät konens radie och höjd. Radien är avståndet från mitten av den cirkulära basen till kanten av basen. Höjd är avståndet från mitten av basen till spetsen av konen, mätt genom mitten av konen.

3. Beräkna lutningshöjden (l) av konen. Eftersom den sneda höjden är den faktiska hypotenusan i en triangel måste du hitta med hjälp av Pythagoras sats för att beräkna det. Använd den omarrangerade formen, l = √ (r + h), varigenom r radien är och h konens höjd.

4. Hitta arean av den cirkulära basen. Arean av basen beräknas med formeln π*r. Efter att ha mätt radien kvadrerar du den (så att du multiplicerar den med sig själv) och sedan multiplicerar du produkten med pi.

5. Beräkna arean av toppen av konen. Använd formeln π*rl, där r radien är av cirkeln och l lutningen som beräknats ovan, för att bestämma arean på toppen av konen.

6. Lägg ihop de två områdena för att få den totala arean av konen. Beräkna den slutliga arean av konen genom att lägga till arean av den cirkulära basen när du beräknar föregående steg.
Förnödenheter
- Linjal
- Penna eller penna
- Papper
Оцените, пожалуйста статью