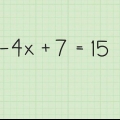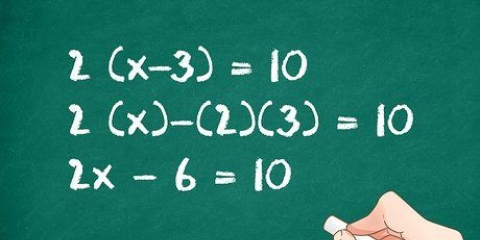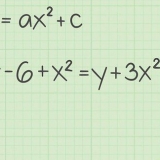3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3(x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Split square
Kvadring är en användbar teknik för att skriva om en andragradsekvation som gör det lättare att övervaka och lösa. Du kan skriva om en ruta genom att ordna om den till mer hanterbara bitar.
Steg
Metod 1 av 2: Del ett: Skriva om en standardekvation

1. Skriv ekvationen. Låt oss anta att du vill lösa följande ekvation: 3x - 4x + 5.

2. Ta bort koefficienten från ekvationen. Placera de 3 yttre parenteserna och dividera varje term utom konstanten med 3. 3x dividerat med 3 är x och 4x dividerat med 3 är 4/3x. Så den nya ekvationen ser ut så här: 3(x - 4/3x) + 5. 5:an är utanför parentesen eftersom du inte har dividerat den med 3.

3. Dividera den andra termen med 2 och kvadrat. Den andra termen, även kallad b-termen i ekvationen är 4/3. Halvera andra terminen. 4/3 ÷ 2, eller 4/3 x 1/2, är lika med 2/3. Kvadrera denna term genom att multiplicera både täljaren och nämnaren med sig själva. (2/3) = 4/9. Skriv ner denna term.

4. Addition och subtraktion. du har detta"ytterligare" term som behövs för att omvandla de tre första termerna i ekvationen till en kvadrat. Men kom ihåg att du lade till denna term genom att också subtrahera den från ekvationen. Naturligtvis gör det liten skillnad att helt enkelt kombinera termerna igen - då är du tillbaka där du började. Den nya ekvationen ska nu se ut så här: 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Få termen du subtraherade utanför parentes. Eftersom du redan arbetar med 3:orna utanför parentesen går det inte att bara sätta -4/9 utanför parentesen. Först måste du multiplicera det med 3. -4/9 x 3 = -12/9, eller -4/3. Om du har att göra med en ekvation som bara innehåller en koefficient 1 ofx, kan du hoppa över detta steg.

6. Konvertera termerna inom parentes till en kvadrat. Din ekvation ser nu ut så här: 3(x -4/3x +4/9). Du arbetade fram och bak för att få 4/9, vilket faktiskt är ett annat sätt att hitta faktorn som fullbordar kvadraten. Så du kan skriva om dessa termer som: 3(x - 2/3). Du kan kontrollera detta genom att multiplicera där du ser att du får samma ursprungliga ekvation som svaret igen.


7. Slå samman konstanterna. Du har nu två konstanter, 3(x - 2/3) - 4/3 + 5. Allt du behöver göra nu är att lägga till -4/3 till 5 och detta ger 11/3 som svar. Du gör detta genom att ge dem samma nämnare: -4/3 och 15/3, och sedan lägga till båda täljarna för att få 11, hålla nämnaren lika med 3.


8. Skriv ekvationen i en annan form. Nu är du klar. Den slutliga ekvationen är 3(x - 2/3) + 11/3. Du kan eliminera 3:an genom att dividera ekvationen med 3, vilket ger dig följande ekvation:(x - 2/3) + 11/9.Du har nu framgångsrikt skrivit ekvationen i en annan form: a(x - h) + k, varigenom k konstanten är.
Metod 2 av 2: Del två: Lösa en andragradsekvation

1. Notera uppgiften. Låt oss anta att du vill lösa följande ekvation: 3x + 4x + 5 = 6

2. Lägg ihop konstanterna och placera dem till vänster om likhetstecknet. Konstanta termer är termer utan variabel. I det här fallet har du 5 till vänster och 6 till höger. Du vill flytta 6 åt vänster, så subtrahera 6 från båda sidor av ekvationen. Detta lämnar 0 till höger (6-6) och -1 till vänster (5-6). Ekvationen ser nu ut så här: 3x + 4x - 1 = 0.

3. Ta kvadratens koefficient utanför parenteserna. I detta fall är 3 koefficienten för x. För att utesluta 3 från parentes, ta bort 3, placera den återstående termen inom parentes och dividera varje term med 3. Så, 3x ÷ 3 = x, 4x ÷ 3 = 4/3x och 1 ÷ 3 = 1/3. Ekvationen ser nu ut så här: 3(x + 4/3x - 1/3) = 0.

4. Dividera med konstanten du just satt inom parentes. Med detta blir du äntligen av med de där irriterande 3:orna utanför fästena. Genom att dividera varje term med 3 kan den elimineras utan att ändra ekvationen. Nu har du: x + 4/3x - 1/3 = 0

5. Dividera den andra termen med 2 och kvadrat. Ta nu andra terminen, 4/3, de b term och dividera med 2. 4/3 2 eller 4/3 x 1/2, är 4/6 eller 2/3. Och 2/3 i kvadrat är 4/9. När du är klar med detta bör du skriva det till vänster och höger om ekvationen eftersom du i princip precis lagt till en ny term. Du måste göra detta på båda sidor av ekvationen. Ekvationen ser nu ut så här: x + 4/3 x + 2/3 - 1/3 = 2/3

6. Flytta den ursprungliga konstanten till höger sida av ekvationen och lägg till den till termen som redan finns där. Flytta konstanten, -1/3, åt höger för att göra den till 1/3. Lägg till detta till den andra termen, 4/9 eller 2/3. Hitta den minsta gemensamma multipeln så att 1/3 och 4/9 kan adderas. Det går så här: 1/3 x 3/3 = 3/9. Lägg nu till 3/9 till 4/9 så att du har 7/9 på höger sida av ekvationen. Detta ger: x + 4/3 x + 2/3 = 4/9 + 1/3 och sedan x + 4/3 x + 2/3 = 7/9.

7. Skriv vänster sida av ekvationen som en kvadrat. Eftersom du redan har använt en formel för att hitta den saknade termen, är det svåraste redan gjort. Allt du behöver göra är att sätta x och hälften av den andra koefficienten inom parentes och kvadrera den, så här :(x + 2/3). Observera att faktorisering av kvadraten ger 3 termer: x + 4/3 x + 4/9. Ekvationen ser nu ut så här: (x + 2/3) = 7/9.

8. Ta kvadratroten från båda sidor av ekvationen. På vänster sida av ekvationen är kvadratroten ur (x + 2/3) lika med x + 2/3. Den högra sidan ger +/- (√7)/3. Kvadratroten ur nämnaren 9 är 3 och kvadratroten ur 7 är √7. Glöm inte att skriva +/- eftersom en kvadratrot ur ett tal kan vara positiv eller negativ.

9. Lägg variabeln åt sidan. För att isolera variabeln x från resten, flytta konstanten 2/3 till höger sida av ekvationen. Du har nu två möjliga svar för x:+/- (√7)/3 - 2/3. Det här är dina två svar. Du kan lämna det så här eller utveckla kvadratroten, om du tillfrågas om ett svar utan radikal.
Tips
- Se till att du sätter +/- på rätt ställen annars får du bara ett svar.
- Även om du kan kvadratrotsformeln kan det inte skada att öva på att dividera kvadrater eller räkna ut andragradsekvationer då och då. På så sätt vet du säkert att du vet hur du gör när det är nödvändigt.
Оцените, пожалуйста статью