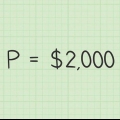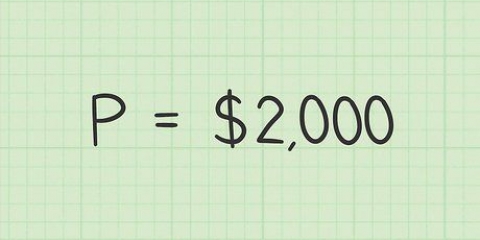Kapitalet (P) är det första beloppet som sätts in på kontot eller det aktuella beloppet som du antar för att göra ränteberäkningen. Räntan (r) måste vara i decimalform. En ränta på 3 % måste anges som 0,03. För att göra detta, dividera den angivna räntan med 100. Värdet på (n) är antalet gånger per år som räntan beräknas och läggs till ditt saldo (även känt som sammansättning). Räntan sammansätts vanligtvis månadsvis (n=12), kvartalsvis (n=4) eller årligen (n=1), men det kan finnas andra alternativ beroende på dina specifika kontovillkor. 
Daglig sammansättningsränta bestäms på liknande sätt, förutom att du då skulle ersätta 4:an som används ovan för variabel(er) med 365. 
Detta förenklas ytterligare genom att lösa termen inom parentes,  . Ekvationen ser nu ut så här:
. Ekvationen ser nu ut så här:  .
. 
Observera att detta är något högre än  , som du kanske hade förväntat dig när du lämnade in den årliga räntan. Detta illustrerar vikten av att förstå hur och när ditt intresse förvärras!
, som du kanske hade förväntat dig när du lämnade in den årliga räntan. Detta illustrerar vikten av att förstå hur och när ditt intresse förvärras! Räntan är skillnaden mellan A och P, så den totala intjänade sammansatta räntan är  .
. 


Kapitalet eller det stora "P" representerar saldot på kontot det datum då du påbörjar beräkningen. Räntesatsen `r` representerar den ränta som betalas på kontot varje år. Det måste uttryckas som ett decimaltal i ekvationen. Det vill säga en ränta på 3 % noteras som 0,03. Du får detta tal genom att dividera den angivna procentsatsen med 100. Värdet `n` representerar antalet gånger räntan höjs årligen. Detta är 365 med en daglig, 12 månad och 4 med en sammansatt ränta per kvartal. Värdet för `t` representerar antalet år under vilka du beräknar den framtida räntan. Detta är antalet år eller del av ett år, om du antar mindre än ett år (t.ex. 0,0833 (1/12) för en månad). 









Funktionen "framtida värde" är utformad för att förskottsbetala ett kontosaldo när det fortsätter att ackumulera ränta, snarare än med ackumulerande sparränta. Som ett resultat returnerar den automatiskt ett negativt tal. Du kan motverka detta problem genom att skriva: 
TW-funktionen tar liknande dataparametrar, separerade med kommatecken, men inte exakt samma. Till exempel: "intresse" syftar på  (den årliga räntan dividerad med `n`). Detta kommer automatiskt att beräkna termerna inom parentes för TW-funktionen.
(den årliga räntan dividerad med `n`). Detta kommer automatiskt att beräkna termerna inom parentes för TW-funktionen. Parametern "antal avbetalningar" avser variabeln  det totala antalet avbetalningar över vilka ackumulationen beräknas och det totala antalet betalningar. Med andra ord, om din PMT inte är 0, kommer VA-funktionen att anta att du lägger till PMT-beloppet över varje period, enligt definitionen av "antal avbetalningar".
det totala antalet avbetalningar över vilka ackumulationen beräknas och det totala antalet betalningar. Med andra ord, om din PMT inte är 0, kommer VA-funktionen att anta att du lägger till PMT-beloppet över varje period, enligt definitionen av "antal avbetalningar". Observera att den här funktionen vanligtvis används för att (till exempel) beräkna hur huvudstolen på ett bolån har betalat sig över tid, genom regelbundna betalningar. Till exempel, om du planerar att betala varje månad i fem år, blir "antal avbetalningar" 60 (5 år x 12 månader). `Sats` är ditt vanliga bidrag under hela perioden (ett bidrag per `n`) `[hw]` (aktuellt värde) är huvudbeloppet - ingående saldo på ditt konto. Den sista variabeln, `[typ_nummer]` kan lämnas tom för denna beräkning (i vilket fall funktionen ställer den automatiskt till 0). TW-funktionen erbjuder möjligheten att göra några grundläggande beräkningar inom funktionsparametrarna, till exempel kan den fullständiga funktionen TW se ut så här:  . Detta indikerar en årlig ränta på 5 % sammansatt månadsvis i 12 månader, under vilken period du sätter in 100 USD/månad med ett ingående saldo (kapitalbelopp) på 5 000 USD. Svaret på den här funktionen ger dig kontosaldot efter 1 år (6483,70 €).
. Detta indikerar en årlig ränta på 5 % sammansatt månadsvis i 12 månader, under vilken period du sätter in 100 USD/månad med ett ingående saldo (kapitalbelopp) på 5 000 USD. Svaret på den här funktionen ger dig kontosaldot efter 1 år (6483,70 €).
Beräkna ränta på ett sparkonto
Även om räntan på sparinlåning ibland är lätt att beräkna genom att multiplicera räntan med ingående saldo, är det i de flesta fall inte så lätt. Till exempel: många sparkonton anger ränta på årsbasis, men beräknar sammansatt ränta varje månad. Varje månad beräknas en bråkdel av årsräntan och läggs till ditt saldo, vilket i sin tur påverkar beräkningen av följande månader. Den här räntecykeln, där räntan beräknas i steg och läggs till ditt saldo kontinuerligt, kallas ränta och det enklaste sättet att beräkna det framtida saldot är att använda en räntesatsformel. Läs vidare för att lära dig detaljerna i dessa typer av ränteberäkningar.
Steg
Metod 1 av 3: Beräkna ränta

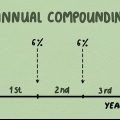
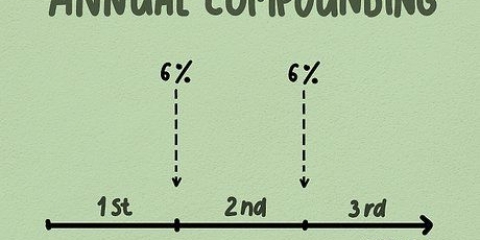
1. Känna till formeln för att beräkna effekten av ränta. Formeln för att beräkna sammansatt ränteackumulering på ett givet saldo är:  .
.
 .
. - (P) är kapitalet, (r) är den årliga räntan och (n) är antalet gånger räntan höjs per år. (A) är saldot som du beräknar, inklusive effekterna av räntan.
- (t) representerar de perioder under vilka räntan har uppkommit. Den måste motsvara den ränta du antar (om det till exempel är årlig ränta måste (t) vara ett antal år som en bråkdel). För att visa det korrekta antalet år som en bråkdel över en tidsperiod, dividera det totala antalet månader med 12, eller dividera det totala antalet dagar med 365.

2. Bestäm variablerna som används i formeln. Läs villkoren för ditt privata konto eller kontakta en anställd på din bank för att slutföra jämförelsen.

3. Koppla in dina värden i formeln. När du har bestämt värdena för varje variabel kan du ange dem i formeln för sammansatt ränta för att bestämma räntan över den angivna tidsskalan. Till exempel, med värdena P=1000, r=0,05 (5%), n=4 (sammanställt per kvartal) och t=1 år får vi följande ekvation:  .
.
 .
.
4. Gör beräkningen. Nu när siffrorna har skrivits in är det dags att lösa formeln. Börja med att förenkla de enkla delarna av ekvationen. Dividera den årliga räntan med antalet avbetalningar för att få den periodiska räntan (i det här fallet  ) och lös målet
) och lös målet  vilken just här
vilken just här  är. Detta resulterar i följande ekvation:
är. Detta resulterar i följande ekvation:  .
.
 ) och lös målet
) och lös målet  vilken just här
vilken just här  är. Detta resulterar i följande ekvation:
är. Detta resulterar i följande ekvation:  .
. . Ekvationen ser nu ut så här:
. Ekvationen ser nu ut så här:  .
.
5. Lös ekvationen. Lös sedan exponenten genom att höja det sista steget till styrkan fyra (dvs  ). Detta levererar
). Detta levererar  som ett resultat på. Ekvationen är nu:
som ett resultat på. Ekvationen är nu:  . Multiplicera dessa två siffror och du får
. Multiplicera dessa två siffror och du får  . Detta är värdet på ditt konto med 5% ränta (sammansatt per kvartal) efter ett år.
. Detta är värdet på ditt konto med 5% ränta (sammansatt per kvartal) efter ett år.
 ). Detta levererar
). Detta levererar  som ett resultat på. Ekvationen är nu:
som ett resultat på. Ekvationen är nu:  . Multiplicera dessa två siffror och du får
. Multiplicera dessa två siffror och du får  . Detta är värdet på ditt konto med 5% ränta (sammansatt per kvartal) efter ett år.
. Detta är värdet på ditt konto med 5% ränta (sammansatt per kvartal) efter ett år. , som du kanske hade förväntat dig när du lämnade in den årliga räntan. Detta illustrerar vikten av att förstå hur och när ditt intresse förvärras!
, som du kanske hade förväntat dig när du lämnade in den årliga räntan. Detta illustrerar vikten av att förstå hur och när ditt intresse förvärras! .
.Metod 2 av 3: Beräkna ränta med periodiska bidrag

1. Använd först formeln för ackumulerad ränta. Du kan även räkna ut ränta på ett konto som du överför regelbundna månadsavgifter till. Detta är användbart om du sparar en viss summa varje månad och sätter in pengarna på ditt sparkonto. Hela ekvationen ser ut så här: 

- Ett enkelt tillvägagångssätt är att skilja den sammansatta räntan på kapitalbeloppet från räntan på de månatliga bidragen (eller betalningarna/PMT). För att komma igång, beräkna först räntan på kapitalet eller kapitalet med hjälp av formeln för ackumulerat sparande.
- Som beskrivs med denna formel kan du beräkna räntan på ditt sparkonto med återkommande månatliga insättningar och sammansatt ränta dagligen, månadsvis eller kvartalsvis.

2. Använd den andra delen av formeln för att beräkna räntan på dina insättningar. (PMT) representerar beloppet på din månatliga insättning.

3. Bestäm dina variabler. Kontrollera ditt konto eller investeringsavtal för att hitta följande variabler: kapital `P`, den årliga räntan `r` och antalet avbetalningar per år `n`. Om dessa variabler inte är lätt tillgängliga, kontakta din bank för att begära denna information. Variabeln `t` representerar antalet år (eller delar därav) som ska beräknas över och `PMT` representerar betalningen/bidraget per månad. Värdet `A` representerar det totala värdet på kontot efter en period och insättningar som du väljer.

4. Koppla in dina värden i formeln. Med hjälp av exemplet P=1000, r=0,05 (5%), n=12 (sammanställt månadsvis), t=3 år och PMT=100, får vi följande ekvation: 


5. Förenkla ekvationen. Börja förenkla målet  om möjligt genom att dividera räntan, 0,05, med 12. Detta är förenklat
om möjligt genom att dividera räntan, 0,05, med 12. Detta är förenklat  Du kan också förenkla genom att lägga till en till räntan inom parentesen. Ekvationen ser nu ut så här:
Du kan också förenkla genom att lägga till en till räntan inom parentesen. Ekvationen ser nu ut så här: 
 om möjligt genom att dividera räntan, 0,05, med 12. Detta är förenklat
om möjligt genom att dividera räntan, 0,05, med 12. Detta är förenklat  Du kan också förenkla genom att lägga till en till räntan inom parentesen. Ekvationen ser nu ut så här:
Du kan också förenkla genom att lägga till en till räntan inom parentesen. Ekvationen ser nu ut så här: 

6. Lös exponenterna. Lös först termerna inuti exponenterna,  , Således
, Således  . Lös sedan exponenterna för att förenkla ekvationen till
. Lös sedan exponenterna för att förenkla ekvationen till  Förenkla genom att subtrahera en och du får
Förenkla genom att subtrahera en och du får 
 , Således
, Således  . Lös sedan exponenterna för att förenkla ekvationen till
. Lös sedan exponenterna för att förenkla ekvationen till  Förenkla genom att subtrahera en och du får
Förenkla genom att subtrahera en och du får 

7. Gör de sista beräkningarna. Multiplicera den första delen av ekvationen och du får $1 616. Lös den andra delen av ekvationen genom att först dividera täljaren med bråkets nämnare, så får du  . Multiplicera detta tal med värdet på insättningen (i detta fall $100) för att få den andra delen av ekvationen. Ekvationen är nu:
. Multiplicera detta tal med värdet på insättningen (i detta fall $100) för att få den andra delen av ekvationen. Ekvationen är nu:  . Kontosaldot är nu under dessa omständigheter
. Kontosaldot är nu under dessa omständigheter  .
.
 . Multiplicera detta tal med värdet på insättningen (i detta fall $100) för att få den andra delen av ekvationen. Ekvationen är nu:
. Multiplicera detta tal med värdet på insättningen (i detta fall $100) för att få den andra delen av ekvationen. Ekvationen är nu:  . Kontosaldot är nu under dessa omständigheter
. Kontosaldot är nu under dessa omständigheter  .
.
8. Beräkna din totala intjänade ränta. I denna ekvation är den faktiska räntan det totala beloppet (A) minus kapitalbeloppet (P) och antalet betalningar gånger insättningen (PMT*n*t). Så i exemplet:  och efter det
och efter det  .
.
 och efter det
och efter det  .
.Metod 3 av 3: Använd ett kalkylblad för att beräkna sammansatt ränta

1. Öppna ett nytt kalkylblad. Excel och liknande kalkylarksprogram (t.ex. Google Sheets) kan spara tid på att göra dessa beräkningar åt dig, och till och med tillhandahålla genvägar i form av inbyggda ekonomifunktioner för att hjälpa dig att beräkna sammansatt ränta.

2. Namnge dina variabler. När du använder ett kalkylblad är det alltid bra att vara så organiserad och tydlig som möjligt. Börja med att namnge en kolumn med celler med den viktiga information du kommer att använda i din beräkning (t.ex. ränta, kapital, tid, n, insättningar).

3. Ange dina variabler. Ange nu informationen du har om ditt specifika konto i nästa kolumn. Detta gör inte bara arbetsbladet lättare att läsa och tolka senare, det lämnar också utrymme för dig att ändra en eller flera av variablerna vid ett senare tillfälle, för att titta på olika möjliga besparingsscenarier.

4. Ställ in din ekvation. Nästa steg är att ange din egen version av ekvationen för upplupen ränta (  ), eller den utökade versionen som tar hänsyn till dina vanliga månatliga insättningar (
), eller den utökade versionen som tar hänsyn till dina vanliga månatliga insättningar (  ). Använd valfri tom cell, börja med ett `=` och använd normala matematiska konventioner (parenteser vid behov) för att ange korrekt ekvation. Istället för att ange variabler som (P) och (n), skriv in motsvarande namn på cellen där du lagrade datavärdena, eller klicka bara på önskad cell medan du redigerar din ekvation.
). Använd valfri tom cell, börja med ett `=` och använd normala matematiska konventioner (parenteser vid behov) för att ange korrekt ekvation. Istället för att ange variabler som (P) och (n), skriv in motsvarande namn på cellen där du lagrade datavärdena, eller klicka bara på önskad cell medan du redigerar din ekvation.
 ), eller den utökade versionen som tar hänsyn till dina vanliga månatliga insättningar (
), eller den utökade versionen som tar hänsyn till dina vanliga månatliga insättningar (  ). Använd valfri tom cell, börja med ett `=` och använd normala matematiska konventioner (parenteser vid behov) för att ange korrekt ekvation. Istället för att ange variabler som (P) och (n), skriv in motsvarande namn på cellen där du lagrade datavärdena, eller klicka bara på önskad cell medan du redigerar din ekvation.
). Använd valfri tom cell, börja med ett `=` och använd normala matematiska konventioner (parenteser vid behov) för att ange korrekt ekvation. Istället för att ange variabler som (P) och (n), skriv in motsvarande namn på cellen där du lagrade datavärdena, eller klicka bara på önskad cell medan du redigerar din ekvation.
5. Använd ekonomifunktioner. Excel erbjuder även vissa ekonomiska funktioner som kan hjälpa dig med din beräkning. Särskilt `future value` (TW) kan användas eftersom det beräknar värdet på ett konto någon gång i framtiden, givet samma variabler som du har blivit van vid nu. För att komma åt den här funktionen gå till en tom cell och skriv `=TW(`. Excel visar sedan en hjälpruta när du öppnar funktionsparentesen för att hjälpa dig att ange rätt parametrar för funktionen.

 (den årliga räntan dividerad med `n`). Detta kommer automatiskt att beräkna termerna inom parentes för TW-funktionen.
(den årliga räntan dividerad med `n`). Detta kommer automatiskt att beräkna termerna inom parentes för TW-funktionen. det totala antalet avbetalningar över vilka ackumulationen beräknas och det totala antalet betalningar. Med andra ord, om din PMT inte är 0, kommer VA-funktionen att anta att du lägger till PMT-beloppet över varje period, enligt definitionen av "antal avbetalningar".
det totala antalet avbetalningar över vilka ackumulationen beräknas och det totala antalet betalningar. Med andra ord, om din PMT inte är 0, kommer VA-funktionen att anta att du lägger till PMT-beloppet över varje period, enligt definitionen av "antal avbetalningar". . Detta indikerar en årlig ränta på 5 % sammansatt månadsvis i 12 månader, under vilken period du sätter in 100 USD/månad med ett ingående saldo (kapitalbelopp) på 5 000 USD. Svaret på den här funktionen ger dig kontosaldot efter 1 år (6483,70 €).
. Detta indikerar en årlig ränta på 5 % sammansatt månadsvis i 12 månader, under vilken period du sätter in 100 USD/månad med ett ingående saldo (kapitalbelopp) på 5 000 USD. Svaret på den här funktionen ger dig kontosaldot efter 1 år (6483,70 €).Tips
- Det är också möjligt, om än mer komplicerat, att beräkna sammansatt ränta på ett konto med oregelbundna betalningar. I denna metod beräknas ränteackumuleringen för varje betalning/bidrag separat (med samma ekvation som beskrivs ovan) och uppnås bäst med ett kalkylblad för att göra beräkningen enklare.
- Du kan också använda en gratis årlig räntekalkylator online för att fastställa räntan på ditt sparkonto. Sök på Internet efter "årlig ränteberäknare" eller "årlig ränteberäknare" för en lista över webbplatser som erbjuder denna tjänst gratis.
"Beräkna ränta på ett sparkonto"
Оцените, пожалуйста статью