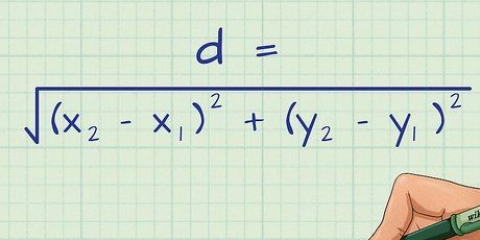Beräkna det absoluta värdet av ett tal: 15 steg (med bilder)

Steg
- Metod 1 av 2: Bestäm absolut värde
- Metod 2 av 2: Lösa komplexa ekvationer med absoluta värden (ekvationer med `i`)
Tips

Absolutvärdet av ett tal är lätt att hitta, och teorin bakom det är viktig för att lösa ekvationer med ett absolut värde. Varje absolutvärde är ett mått på hur långt talet är från noll. Om du tänker på en tallinje, med nollan i mitten, kan du ta reda på hur långt talet i fråga är från den nollan.

Steg

Metod 1 av 2: Bestäm absolut värde

1. Kom ihåg att det absoluta värdet är avståndet mellan ett tal och noll. Ett absolutvärde är avståndet från talet till noll längs en tallinje. antingen,

| - 4 |

${displaystyle |-4|}$ så anger helt enkelt hur långt bort -4 är från noll. Eftersom avstånd alltid är ett positionsnummer (du kan inte röra dig i "negativa" steg, bara i en annan riktning), är resultatet av det absoluta värdet alltid positivt.

Bild med titeln Hitta det absoluta värdet av ett tal Steg 2

2. Gör talet inom de absoluta värdestaplarna positivt. Enkelt uttryckt gör det absoluta värdet vilket tal som helst positivt. Det är användbart för att mäta avstånd, eller bestämma värden i ekonomiska frågor, arbeta med negativa siffror som skulder eller lån.

Bild med titeln Hitta det absoluta värdet av ett tal Steg 3

3. Använd enkla vertikala streck för att indikera ett absolut värde. Formatet för ett absolut värde är enkelt. Enstaka rader (finns nära Enter-tangenten på ett tangentbord) runt ett tal eller uttryck, som t.ex

| n |, | 3 + 5 |, | - 72 |

${displaystyle |n|,|3+5|,|-72|}$ , indikerar ett absolut värde.

| 2 |

${displaystyle |2|}$ är det absoluta värdet av 2.`

Bild med titeln Hitta det absoluta värdet av ett tal Steg 4

4. Utelämna minustecken för siffran inom absolutvärdesmärkena. Till exempel: |-5| blir då |5|.

Bild med titeln Hitta det absoluta värdet av ett tal Steg 5

5. Utelämna absolutvärdesmärkena. Siffran som återstår är svaret, så |-5| blir |5| och sedan 5. Följande är allt du behöver göra:

| - 5 | = 5

${displaystyle |-5|=5}$

Bild med titeln Hitta det absoluta värdet av ett tal Steg 6

6. Förenkla uttrycket inom det absoluta värdet. Är det ett enkelt uttryck, som t.ex

| - 10 |

${displaystyle |-10|}$ , då kan du bara göra det positivt. Men ett uttryck som

| (- 4 * 5) + 3 - 2 |

${displaystyle |(-4*5)+3-2|}$ måste förenklas innan du kan hitta dess absoluta värde. Den fasta ordningen för operationer gäller fortfarande:

Uppdrag:

| (- 4 * 5) + 3 - 2 |

${displaystyle |(-4*5)+3-2|}$

Förenkla inom parentes:

| (- 20) + 3 - 2 |

${displaystyle |(-20)+3-2|}$

Addera och subtrahera:

| - 19 |

${displaystyle |-19|}$

Gör allt inom det absoluta värdet positivt:

| 19 |

${displaystyle |19|}$

Slutligt svar: 19

Bild med titeln Hitta det absoluta värdet av ett tal Steg 7

7. Använd alltid denna ordningsföljd innan du beräknar det absoluta värdet. När du räknar ut längre ekvationer gör du allt som krävs innan du bestämmer det absoluta värdet. Försök inte att förenkla absoluta värden förrän allt har lagts till, subtraherat och delat korrekt. Till exempel:

Uppdrag:

1 + 2 + | 4 - 7 | 5 * | - 3 * 2 |

${displaystyle {frac {1+2+|4-7|}{5*|-3*2|}}}$

Gör operationsordningen inom och utanför det absoluta värdet:

3 + | - 3 | 5 * | - 6 |

${displaystyle {frac {3+|-3|}{5*|-6|}}}$

Bestäm de absoluta värdena:

3 + (3) 5 * (6)

${displaystyle {frac {3+(3)}{5*(6)}}}$

Ordning för operationer:

\frac{6}{30}

${displaystyle {frac {6}{30}}}$

Förenkla det slutliga svaret: $\frac{1}{5}$ ${frac{1}{5}}$

Bild med titeln Hitta det absoluta värdet av ett tal Steg 8

8. Fortsätt arbeta med några exempelövningar för att få kläm på det. Att beräkna det absoluta värdet av ett tal är väldigt enkelt, men det betyder inte att det inte skulle vara till hjälp att göra övningsproblem för att fräscha upp dina kunskaper:

| 12 |

${displaystyle |12|}$ =

12

${displaystyle 12}$

| - 24 |

${displaystyle |-24|}$ =

24

${displaystyle 24}$

| 3 + 2 - 11 + 5 - 6 |

${displaystyle |3+2-11+5-6|}$ =

7

$7$

Metod 2 av 2: Lösa komplexa ekvationer med absoluta värden (ekvationer med `i`)

Bild med titeln Hitta det absoluta värdet av ett tal Steg 9

1. Var försiktig när du hanterar komplexa ekvationer som involverar imaginära tal, som "i" eller -1{displaystyle {sqrt {-1}}} ${displaystyle {sqrt {-1}}}$ , och lösa dem separat. Du kan inte hitta absolutvärdet av imaginära tal på samma sätt som du kan hitta rationella tal. Du kan hitta det absoluta värdet av en komplex ekvation genom att räkna ut det i avståndsformeln. Ta uttrycket

| 3 - 4 i |

${displaystyle |3-4i|}$ som ett exempel.

Uppdrag: $| 3 - 4 i |$ ${displaystyle |3-4i|}$
Var uppmärksam: Om du använder ett uttryck som $\sqrt{- 1}$ ${displaystyle {sqrt {-1}}}$ du kan ersätta den med `i.` Kvadratroten ur -1 är ett imaginärt tal, dvs. $| i | = 1$ ${displaystyle |i|=1}$

Bild med titeln Hitta det absoluta värdet av ett tal Steg 10

2. Hitta koefficienterna för den komplexa ekvationen. Ta 3-4i som ekvationen för en linje. Det absoluta värdet är avståndet till noll, så du bestämmer avståndet till noll för punkten (3, -4) på denna linje.Koefficienterna är helt enkelt de två talen som inte är `i`. Även om talet bredvid i-et vanligtvis är det andra talet, spelar det ingen roll när man löser. Öva detta med följande koefficienter:

| 1 + 6 i |

${displaystyle |1+6i|}$ = (1, 6)

| 2 - i |

${displaystyle |2-i|}$ = (2, -1)

| 6 i - 8 |

${displaystyle |6i-8|}$ = (-8, 6)

Bild med titeln Hitta det absoluta värdet av ett tal Steg 11

3. Ta bort absolutvärdessymbolerna från ekvationen. Nu behöver du bara koefficienterna. Kom ihåg att du bestämmer ekvationens avstånd från noll. Eftersom du kommer att använda distansformeln i nästa steg, är detta samma sak som att bestämma det absoluta värdet.

Bild med titeln Hitta det absoluta värdet av ett tal Steg 12

4. Kvadrera båda koefficienterna. För att bestämma avståndet använder du avståndsformeln, även känd som

\sqrt{X} 2 + y^{2}

${displaystyle {sqrt {x^{2}+y^{2}}}}$ . Så som ett första steg måste du kvadrera båda koefficienterna för den komplexa ekvationen. Vi fortsätter med exemplet:

| 3 - 4 i |

${displaystyle |3-4i|}$ :

Koefficienter: (3, -4)

Avståndsformel:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Kvadrera koefficienterna: `

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Var uppmärksam: Öva på distansformeln igen om du inte förstår den. Observera att kvadrera båda siffrorna gör dem positiva, vilket i huvudsak ger dig det absoluta värdet.

Bild med titeln Hitta det absoluta värdet av ett tal Steg 13

5. Placera produkten av talen under radikalen. Det radikala tecknet indikerar att du subtraherar kvadratroten av talet under det. Lägg nu ihop siffrorna först, utan att göra något åt det radikala tecknet.

Koefficienter: (3, -4)

Avståndsformel:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Kvadrera koefficienterna:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Lägg till produkten av koefficienterna:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Bild med titeln Hitta det absoluta värdet av ett tal Steg 14

6. Ta kvadratroten för ditt slutliga svar. Du behöver bara förenkla ekvationen för det slutliga svaret. Detta är avståndet från din `punkt` på en tänkt tallinje till nollpunkten. Om det inte finns någon kvadratrot, lämna bara svaret från det sista steget under det radikala tecknet - detta är ett korrekt svar.

Koefficienter: (3, -4)

Avståndsformel:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Kvadrera koefficienterna:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Lägg till produkten av koefficienterna:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Subtrahera kvadratroten för det slutliga svaret: 5

$| 3 - 4 i | = 5$ ${displaystyle |3-4i|=5}$

Bild med titeln Hitta det absoluta värdet av ett tal Steg 15

7. Prova några övningar. Klicka med musen direkt bakom frågorna för att se svaren i vitt.

| 1 + 6 i |

${displaystyle |1+6i|}$ = √37

| 2 - i |

${displaystyle |2-i|}$ = √5

| 6 i - 8 |

${displaystyle |6i-8|}$ = 10

Tips

Om du har en variabel inom ett absolutvärde kan du inte ta bort absolutvärdetecknen med den här metoden, för om värdet på variabeln är negativt så skulle det absoluta värdet göra det positivt.
Om du har ett uttryck inom ett absolut värde, förenkla uttrycket innan du bestämmer dess absoluta värde.
När ett positivt tal är inom de absoluta värdemarkörerna är svaret alltid det talet.
Du behöver en annan metod för att lösa absolutvärdesekvationer med ett x och y, även om teorin bakom det absoluta värdet används som grund.
Ett absolut värde kan aldrig vara ett negativt tal, så om du ser något som | 2 - 4x| = -7, då vet du att denna ekvation är falsk utan att behöva lösa den.