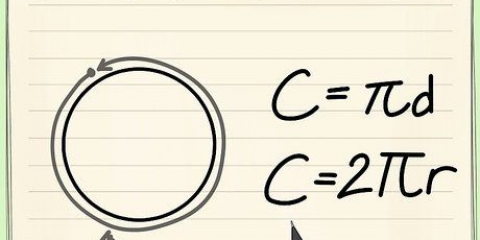Låt oss säga att cirkelns yta är 500 cm. Sedan räknar du ut ekvationen enligt följande: 2√3,14 x 500. 
Om beräkningen är lika med 2√3,14 x 500, så beräknar du först 3,14 x 500 = 1570. Beräkna sedan 2√1 570. 
Kvadratroten från 1570 är 39,6. 
Beräkna 39,6 x 2 = 79,2. Det betyder att omkretsen är 79,2 cm, vilket löser formeln. 

Antag att cirkelns yta är 200 cm. Ekvationen blir då 200 = 3,14 x R. 
Om du delar 200 med 3,14 blir resultatet 63,7. Så den nya ekvationen är 63,7 = R. 
Kvadratroten av 63,7 är 7,9. Ekvationen blir då 7,9 = R, vilket betyder att cirkelns radie är 7,9. Detta ger dig all information du behöver för att hitta omkretsen. 
Använd det första alternativet, 7,9 x 2 = 15,8, cirkelns diameter. Denna diameter gånger 3,14 är 49,6. För det andra alternativet blir beräkningen 2 x 3,14 x 7,9. Först räknar du ut 2 x 3,14 = 6,28, och det multiplicerat med 7,9 är 49,6. Lägg märke till hur båda metoderna ger dig samma svar.
Beräkna omkrets med hjälp av area
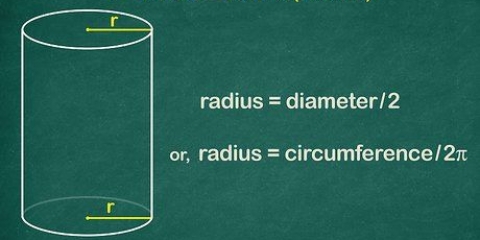
Formeln för att beräkna omkretsen (C) av en cirkel, C = πD eller C = 2πR, är enkel om du känner till cirkelns diameter (D) eller radie (R). Men vad gör du om du bara känner till cirkelns yta? Liksom många saker inom matematik finns det flera lösningar på detta problem. Formeln C = 2√πA är utformad för att hitta omkretsen av en cirkel med hjälp av arean (A). Du kan också vända ekvationen A = πR för att hitta R och sedan skriva in R i perimeterekvationen. Båda ekvationerna ger samma resultat.
Steg
Metod 1 av 2: Använd perimeterekvationen

1. Använd formeln C=2√πA för att lösa problemet. Denna formel beräknar omkretsen av en cirkel om du bara känner till dess area. C står för omkretsen och A för området. Skriv den här formeln för att börja lösa problemet.
- π-symbolen, som står för pi, är en återkommande decimal med (vid det här laget) tusentals siffror efter decimalkomma. För enkelhets skull, använd 3.14 som värdet på pi.
- Eftersom du ändå måste konvertera pi till dess numeriska form, använd 3.14 i ekvationen från början. Skriv det som C = 2√3,14 x A.

2. Inkludera arean som A i ekvationen. Eftersom du redan känner till cirkelns area är det värdet på A. Fortsätt sedan för att lösa problemet med hjälp av operationsordningen.

3. Multiplicera pi med arean av cirkeln. I operationsordningen kommer operationerna inom kvadratrotsymbolen först. Multiplicera pi med arean av cirkeln du kopplade in. Koppla sedan in det resultatet i ekvationen.

4. Särskildroten ur av summan. Det finns flera sätt att beräkna kvadratroten. Om du använder en miniräknare, tryck på funktionen √ och skriv in siffran. Du kan också lösa problemet för hand med hjälp av primtalsfaktorer.

5. Multiplicera kvadratroten med 2 för att hitta omkretsen. Slutligen slutför du beräkningen genom att multiplicera resultatet med 2. Detta returnerar ett slutligt tal, omkretsen.
Metod 2 av 2: Åtgärda problemet omvänt

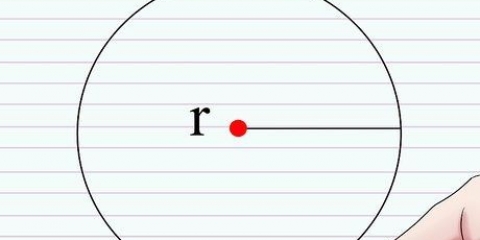
1. Använd formeln A = πR in. Detta är formeln för arean av en cirkel. A står för arean och R för radien. Normalt skulle du använda det om du kände till radien, men du kan också fylla i arean för att lösa ekvationen.
- Återigen, använd 3,14 som det avrundade värdet för pi.

2. Ange området som värde för A. Använd cirkelns area i ekvationen. Placera detta till vänster om ekvationen som värdet för A.

3. Dividera båda sidor av ekvationen med 3,14. För att lösa denna typ av ekvation måste du gradvis eliminera stegen till höger genom att göra motsatta operationer. Eftersom du vet värdet på pi, dividerar du varje sida med det värdet. Detta eliminerar pi till höger och ger dig ett nytt numeriskt värde till vänster.

4. Särskildroten ur av resultatet för att få cirkelns radie. Då elimineras exponenten på höger sida av ekvationen. Motsatsen till `exponentiering` är att hitta kvadratroten ur talet. Hitta kvadratroten av varje sida av ekvationen. Detta tar bort exponenten till höger och placerar radien till vänster.

5.Bestäm omkretsen av cirkeln med hjälp av radien. Det finns två formler för att hitta omkretsen (C). Den första är C = πD, där D är diametern. Multiplicera radien med 2 för att hitta diametern. Den andra är C = 2πR. Multiplicera 3,14 med 2 och multiplicera sedan resultatet med radien. Båda formlerna ger dig samma resultat.
"Beräkna omkrets med hjälp av area"
Оцените, пожалуйста статью