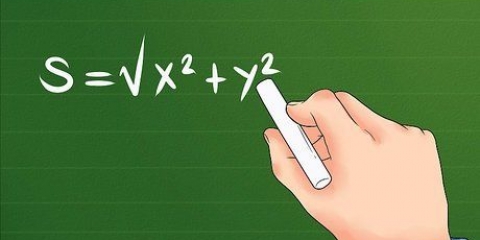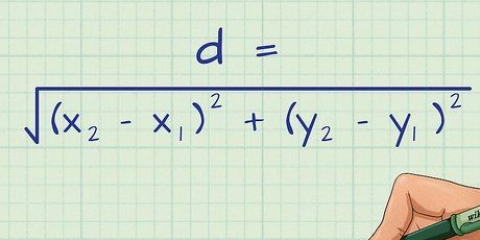Hur man beräknar avståndet mellan två punkter: 6 steg (med bilder)

Steg
Tips

Tänk på avståndet mellan två punkter som en linje. Längden på denna linje kan hittas med avståndsformeln: $\sqrt{(} (X_{2} - X_{1})^{2} + (y_{2} - y_{1})^{2})$ ${sqrt(}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .

Steg

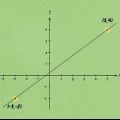
1. Ta koordinaterna för två punkter mellan vilka du vill hitta avståndet. Kalla en punkt 1 (x1,y1) och den andra punkten 2 (x2,y2). Det spelar ingen roll vilken punkt du utgår ifrån, så länge du applicerar etiketterna (1 och 2) konsekvent under hela problemet.

x1 är den horisontella koordinaten (längs x-axeln) för punkt 1, och x2 är den horisontella koordinaten för punkt 2. y1 är den vertikala koordinaten (längs y-axeln) för punkt 1, och y2 är den vertikala koordinaten för punkt 2.
Nej, till exempel punkterna (3.2) och (7.8). Om (3.2) är lika med (x1,y1), så är (7.8) lika med (x2,y2).

Bild med titeln Hitta avståndet mellan två punkter Steg 1

2. Använd avståndsformeln. Denna formel bestämmer längden på en rät linje mellan två punkter: punkt 1 och punkt 2. Det linjära avståndet är kvadratroten av kvadraten på det horisontella avståndet, plus kvadraten på det vertikala avståndet mellan två punkter. Enkelt uttryckt är det kvadratroten av:

(X 2 - X_{1})^{2} + (y_{2} - y_{1})^{2}

$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Bild med titeln Hitta avståndet mellan två punkter Steg 3

3. Bestäm det horisontella och vertikala avståndet mellan punkterna. Beräkna först y2 - y1 för att hitta det vertikala avståndet. Beräkna sedan x2 - x1 för att hitta det horisontella avståndet. Oroa dig inte om subtraktionen ger negativa tal. Nästa steg är att kvadrera dessa värden (vilket alltid resulterar i ett positivt heltal).

Bestäm avståndet längs y-axeln. För exemplet punkterna (3.2) och (7.8), där punkt 1 är (3.2) och punkt 2 (7.8) blir detta: (y2 - y1) = 8 - 2 = 6. Det betyder att avståndet på y-axeln mellan dessa två punkter är sex längdenheter.

Bestäm avståndet längs x-axeln. För samma provpunkter (3.2) och (7.8): (x2 - x1) = 7 - 3 = 4. Det betyder att det finns fyra längdenheter som skiljer de två punkterna på x-axeln åt.

Bild med titeln Hitta avståndet mellan två punkter Steg 4

4. Kvadra båda värdena. Det betyder att du kvadrerar x-axelns avstånd (x2 - x1), och du kvadrerar y-axelns avstånd (y2 - y1).

62 = 36

$6^{2}=36$

42 = 16

$4^{2}=16$

Bild med titeln Hitta avståndet mellan två punkter Steg 5

5. Lägg ihop rutorna. Detta ger dig kvadraten på det diagonala, linjära avståndet mellan dina två punkter. I exemplet med punkterna (3.2) och (7.8) är kvadraten på (7 - 3) 16 och kvadraten på (8 - 2) är 36. 36 + 16 = 52.

Bild med titeln Hitta avståndet mellan två punkter Steg 6

6. Ta kvadratroten ur ekvationen. Detta är det sista steget i ekvationen. Det linjära avståndet mellan de två punkterna är kvadratroten av summan av kvadraterna av avståndet på x-axeln och avståndet på y-axeln.

Om vi fortsätter med exemplet är avståndet mellan (3.2) och (7.8) kvadratroten ur 52, eller ungefär 7.21.

Tips

Det spelar ingen roll om du får ett negativt tal efter att ha subtraherat y2 - y1 eller x2 - x1. Eftersom skillnaden är kvadratisk får du alltid ett positivt avstånd i ditt svar.