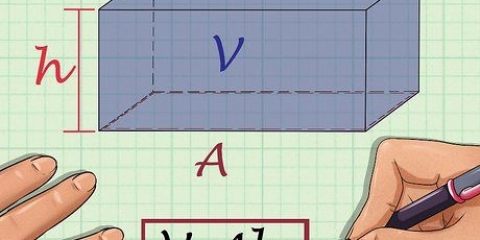
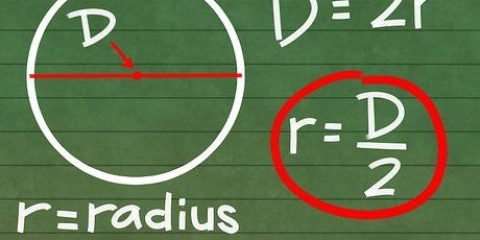
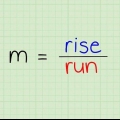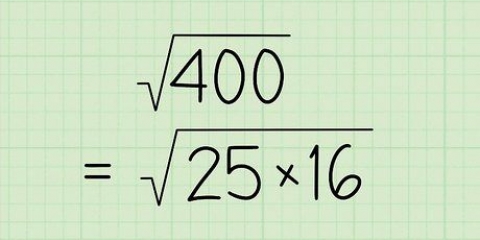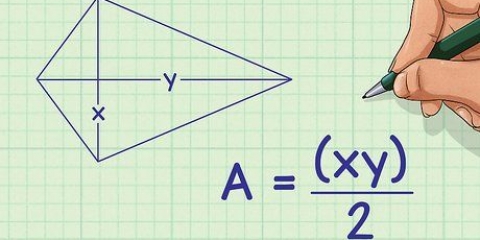X-axeln är den horisontella axeln; y-axeln är den vertikala axeln. Koordinaterna för en punkt skrivs som  .
. Till exempel kan ett linjesegment ha en ändpunkt vid  och en annan på
och en annan på  .
. 
Till exempel med poängen  och
och  , din formel kommer att se ut så här:
, din formel kommer att se ut så här: 


Till exempel:



Till exempel:



Eftersom du bestämmer kvadratroten kan du behöva avrunda ditt svar. Eftersom du arbetar utifrån ett koordinatsystem kommer ditt svar att vara i generella "enheter" och inte i centimeter, meter eller någon annan enhet. Till exempel:

 enheter.
enheter.
Beräkna längden på en linje med avståndsformeln
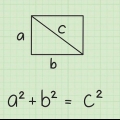
Du kan mäta längden på en vertikal eller horisontell linje i ett koordinatsystem genom att helt enkelt lägga till koordinaterna; det är dock lite svårare att mäta längden på en diagonal linje. Du kan använda avståndsformeln för att bestämma längden på en sådan linje. Denna formel är egentligen Pythagoras sats, vilket blir tydligt när man föreställer sig linjesegmentet som hypotenusan av en rätvinklig triangel. Genom att använda en enkel geometrisk formel blir det en relativt enkel uppgift att mäta linjer längs ett antal koordinater.
Steg
Del 1 av 2: Att skriva formeln

1. Skriv ner avståndsformeln. Formeln säger det  , varigenom
, varigenom  är lika med linjens avstånd,
är lika med linjens avstånd,  är lika med koordinaterna för linjesegmentets första slutpunkt, och
är lika med koordinaterna för linjesegmentets första slutpunkt, och  är lika med koordinaterna för linjesegmentets andra slutpunkt.
är lika med koordinaterna för linjesegmentets andra slutpunkt.
 , varigenom
, varigenom  är lika med linjens avstånd,
är lika med linjens avstånd,  är lika med koordinaterna för linjesegmentets första slutpunkt, och
är lika med koordinaterna för linjesegmentets första slutpunkt, och  är lika med koordinaterna för linjesegmentets andra slutpunkt.
är lika med koordinaterna för linjesegmentets andra slutpunkt.
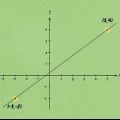
2. Bestäm koordinaterna för ändpunkterna för linjesegmentet. Dessa kan redan ha getts. Om inte, räkna längs x-axeln och y-axeln för att hitta koordinaterna.
 .
. och en annan på
och en annan på  .
.
3. Tillämpa koordinaterna på avståndsformeln. Se till att du anger värdena för rätt variabler. De två  -koordinaterna är inom de första parenteserna, och de två
-koordinaterna är inom de första parenteserna, och de två  -koordinaterna finns inom de nästa två parenteserna.
-koordinaterna finns inom de nästa två parenteserna.
 -koordinaterna är inom de första parenteserna, och de två
-koordinaterna är inom de första parenteserna, och de två  -koordinaterna finns inom de nästa två parenteserna.
-koordinaterna finns inom de nästa två parenteserna. och
och  , din formel kommer att se ut så här:
, din formel kommer att se ut så här: 
Del 2 av 2: Beräkna avståndet

1. Beräkna minussumman inom parentes. Enligt operationsordningen måste varje beräkning inom parentes beräknas först.
- Till exempel:

2. Kvadra värdet inom parentes. I operationsordningen står det att man sedan ska räkna ut potenserna.



3. Lägg till siffrorna under det radikala tecknet. Du kan göra den här beräkningen som om du arbetade med heltal.



4. Lösa åt d  . För att approximera det slutliga svaret, hitta kvadratroten av summan under radikalen.
. För att approximera det slutliga svaret, hitta kvadratroten av summan under radikalen.
 . För att approximera det slutliga svaret, hitta kvadratroten av summan under radikalen.
. För att approximera det slutliga svaret, hitta kvadratroten av summan under radikalen.
 enheter.
enheter.Tips
- Förväxla inte den här formeln med andra, till exempel medelpunktsformeln, lutningsformeln eller ekvationen för en linje.
- Tänk på operationsordningen när du beräknar svaret. Subtrahera först, sedan kvadratisk skillnaden, addera sedan och beräkna sedan kvadratroten.
"Beräkna längden på en linje med avståndsformeln"
Оцените, пожалуйста статью