Denna radie är vinkelrät mot den största radien, men du behöver inte mäta vinklar för detta problem. Du kan också kalla denna radie för `den mindre huvudaxeln`. 
Till exempel, om en ellips har en största radie på 5 och en minsta radie på 3, är ellipsens area 3 x 5 x π, eller ungefär 47 enheter i kvadrat. Om du inte har en miniräknare, eller om din miniräknare inte har en π-symbol, använd `3.14` som värde för pi. 

Beräkna arean av en ellips
En ellips är en tvådimensionell form som du kanske redan känner till från geometriklassen, som ser ut som en långsträckt cirkel. Att beräkna arean av en ellips är lätt när du vet längden på den största radien och den minsta radien.
Steg
Del 1 av 2: Beräkna arean

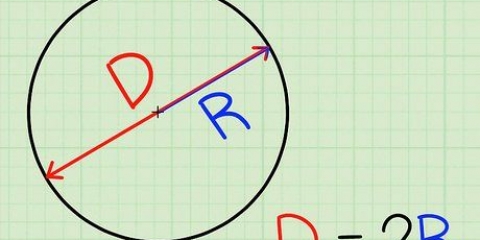
1. Hitta den största radien på ellipsen. Detta är avståndet från mitten av ellipsen till ellipsens yttersta kant. Betrakta detta som radien för den "tjocka" delen av ellipsen. Mät detta eller sök efter lämplig etikett i diagrammet. Vi kallar detta värde a.
- Du kan också kalla detta "huvudaxeln".

2. Hitta den minsta radien. Som du kanske har gissat är den minsta radien avståndet från mitten till den närmaste punkten på kanten. Vi kallar detta värde b.

3. Multiplicera med pi. Området för ellipsen är a X b x. Eftersom du multiplicerar två längdenheter tillsammans är ditt svar en kvadrat.
Del 2 av 2: Förstå varför det fungerar

1. Tänk på arean av en cirkel. Du kanske kommer ihåg att arean av en cirkel är lika med πr, vilket är detsamma som π x r X r. Anta att vi vill bestämma arean av en cirkel som om det vore en ellips? Vi mäter radien i en riktning: r. Mät det med räta vinklar: också r. Tillämpa detta på formeln för arean av en ellips: π x r x r! Det visar sig att en cirkel bara är en specifik typ av ellips.

2. Föreställ dig en tillplattad cirkel. Föreställ dig att en cirkel är tryckt i form av en ellips. När cirkeln komprimeras längre och längre kommer en radie att förkortas och den andra längre. Området förblir detsamma, eftersom ingenting går ut ur cirkeln. Så länge vi använder båda radierna i ekvationen kommer "klämning" och "sträckning" att ta bort varandra och vi får fortfarande rätt svar.
Tips
- Om du vill ha ett matematiskt bevis på detta måste du lära dig integrera.
"Beräkna arean av en ellips"
Оцените, пожалуйста статью