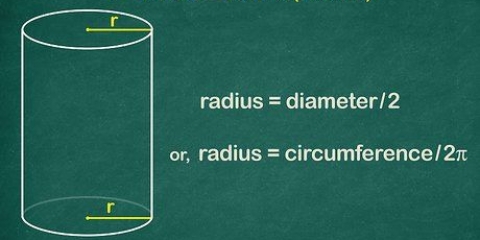
I vårt exempel tar vi kvadratrötterna från 25 och 16. Se nedan: Sqrt(25×16) Sqrt(25) × Sqrt(16) 5 × 4 = 20 
Låt oss ta kvadratroten ur 147 som ett exempel. 147 är inte produkten av två perfekta rutor, så vi kan inte få ett bra heltalsvärde. Men det är produkten av en perfekt kvadrat och ett annat nummer - 49 och 3. Vi kan använda denna information för att skriva vårt svar på de enklaste termerna: sqrt(147) = Sqrt(49 × 3) = Sqrt(49) × Sqrt(3) = 7 × Sqrt(3) 
Låt oss återgå till vårt exempel. Eftersom 2 = 4 och 1 = 1 vet vi att Sqrt(3) är mellan 1 och 2 – förmodligen närmare 2 än 1. Vi uppskattar att 1,7. 7 × 1,7 = 11.9. När vi kollar detta med kalkylatorn ser vi att vi är ganska nära svaret: 12.13. Detta fungerar även för de större siffrorna. Till exempel är Sqrt(35) ungefär mellan 5 och 6 (förmodligen närmare 6). 5 = 25 och 6 = 36. 35 är mellan 25 och 36, så kvadratroten blir mellan 5 och 6. Eftersom 35 är strax under 36, kan vi med viss säkerhet säga att dess kvadratrot bara är lägre än 6. Att kolla med en miniräknare ger oss ett svar på cirka 5,92 – vi hade rätt. 
Ett exempel: vi bestämmer kvadratroten ur 45 med den här metoden. Vi vet att 45 = 9 × 5 och att 9 = 3 × 3. Så vi kan skriva kvadratroten så här: Sqrt(3 × 3 × 5). Ta bara bort 3:orna och placera en 3:a utanför radikalen för att få en förenklad kvadratrot: (3)Sqrt(5). Nu kan du enkelt uppskatta. Ett sista exempel; vi bestämmer kvadratroten ur 88: sqrt(88) = Sqrt(2 × 44) = Sqrt(2 × 4 × 11) = Sqrt(2 × 2 × 2 × 11). Vi har flera 2:or i vår kvadratrot. Eftersom 2 är primtal kan vi ta bort ett par och placera en 2:a utanför kvadratroten. = Vår kvadratrot i enklaste termer är (2) Sqrt(2 × 11) eller (2) Sqrt(2) Sqrt(11). Nu kan vi närma oss Sqrt(2) och Sqrt(11) och hitta ett uppskattat svar, om vi vill. 

I vårt exempel är siffran längst till vänster siffran 7. Eftersom vi vet att 2 = 4 7 < 3 = 9, kan vi säga att n = 2 eftersom det är det största heltal vars kvadrat är mindre än eller lika med 7. Skriv 2 i den övre högra kvadranten. Detta är den första siffran i svaret. Skriv 4 (kvadraten av 2) i den nedre högra kvadranten. Detta nummer är viktigt för nästa steg. 
I vårt exempel skriver vi en 4 under 7 och subtraherar den. Detta ger 3 som ett svar. 
I vårt exempel är följande nummer "80". notera "80" bredvid 3:an i den vänstra kvadranten. Multiplicera sedan talet längst upp till höger med 2. Detta nummer är 2, så 2 × 2 = 4. notera "`4"` längst ner till höger, följt av _×_=. 
I vårt exempel fyller vi i 8, och detta ger 4(8) × 8 = 48 × 8 = 384. Detta är mer än 380. Så 8 är för stort, men 7 är det förmodligen inte. Fyll i 7 och lös: 4(7) × 7 = 329. 7 är bra eftersom 329 är mindre än 380. Not 7 uppe till höger. Detta är den andra siffran i kvadratroten av 780,14. 
I vårt exempel subtraherar vi 329 från 380, och detta ger 51 som resultat. 
I vårt svar skriver vi nu ett kommatecken eftersom vi även stöter på detta i 780.14. Flytta nästa par (14) ner i den vänstra kvadranten. 27 x 2 = 54, så vi skriver "54 _×_=" i den nedre högra kvadranten. 
I vårt exempel är 549 × 9 = 4941, vilket är mindre än eller lika med siffran till vänster (5114). 549 × 10 = 5490, vilket är för högt, så 9 är vårt svar. Skriv 9 som nästa tal längst upp till höger och subtrahera multiplikationsresultatet från det vänstra talet: 5114 -4941 = 173. 
Beräkna kvadratroten ur ett tal utan miniräknare
Innan miniräknarens tillkomst var både studenter och professorer tvungna att beräkna kvadratrötter med penna och papper. Olika tekniker har utvecklats vid den tiden för att ta itu med denna ibland tunga uppgift, där vissa ger en grov uppskattning och andra beräknar det exakta värdet. Läs vidare för att lära dig hur du hittar kvadratroten ur ett tal i några enkla steg.
Steg
Metod 1 av 2: Rooting med primfaktorer

1. Dela upp ditt nummer i rutor. Den här metoden använder faktorerna för ett tal för att hitta kvadratroten ur ett tal (beroende på antalet kan detta vara ett exakt svar eller en uppskattning). De faktorer av ett givet tal är en slumpmässig sekvens av tal multiplicerade tillsammans för att bilda det specifika talet. Till exempel kan du säga att faktorerna 8 är lika med 2 och 4 eftersom 2 × 4 = 8. Perfekta kvadrater, å andra sidan, är heltal som är produkten av andra heltal. Till exempel: 25, 36 och 49 är perfekta kvadrater eftersom de är lika med 5, 6 respektive 7. Andra potensfaktorer är, som du säkert har förstått, faktorer som också är perfekta rutor. För att hitta en kvadratrot med primtalsfaktorer, prova först att dela talet i dess kubfaktorer.
- Ta följande exempel. Vi ska hitta kvadratroten av 400. Till att börja med delar vi upp talet i rutor. Eftersom 400 är en multipel av 100 vet vi att den är jämnt delbar med 25 - en perfekt kvadrat. Snabb memorering säger oss att 400 / 25 = 16. 16 råkar också vara en perfekt ruta. Så de kvadratiska faktorerna på 400 är 25 och 16 eftersom 25 × 16 = 400.
- Vi skriver detta som: Sqrt(400) = Sqrt(25 × 16)

2. Ta kvadratrötterna av dina kvadratrötter. Produktregeln för kvadratrötter säger att för ett givet tal a och b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). På grund av denna egenskap kan vi nu ta kvadratrötterna av kubfaktorerna och multiplicera dem för svaret.

3. Om ditt nummer inte kan faktoriseras helt perfekt, förenkla det. I verkligheten kommer talen du vill hitta kvadratrötterna av inte att vara snygga avrundade tal med fina kvadratrötter som 400. I dessa fall kanske det inte går att få ett heltal som svar. Med hjälp av alla kuber du kan hitta kan du istället bestämma svaret som en mindre, enklare att använda kvadratrot. Du gör detta genom att reducera talet till en kombination av kubfaktorer och andra faktorer och sedan förenkla det.

4. Förenkla vid behov. Med kvadratroten i de enklaste termerna är det vanligtvis ganska lätt att få en grov uppskattning av svaret genom att uppskatta de återstående kvadratrötterna och multiplicera dem. Ett sätt att förbättra dina gissningar är att hitta de perfekta kvadraterna på vardera sidan av talet i din kvadratrot. Du vet att decimalvärdet för talet i din kvadratrot är någonstans mellan dessa två siffror, så din gissning bör också ligga mellan dessa tal.

5. Alternativt, som ett första steg, kan du förenkla numret tillminsta gemensamma nämnare. Sökandet efter kvadratfaktorer är inte nödvändigt om du enkelt kan hitta primtalsfaktorerna för ett tal (faktorer som samtidigt är primtal). Skriv talet i termer av minsta gemensamma multipel. Sök sedan bland dina faktorer efter motsvarande par av primtal. Om du hittar två primtalsfaktorer som matchar, ta bort dem från kvadratroten och sätt a av dessa siffror utanför radikalen.
Metod 2 av 2: Hitta kvadratrötter utan miniräknare
Med en lång division

1. Dela upp siffrorna i ditt nummer i par. Denna metod liknar lång division, vilket gör att du kan exakt hitta kvadratroten ur ett tal siffra för siffra. Även om det inte är nödvändigt, kan det göra det lättare att lösa upp ett nummer i användbara bitar, särskilt om det är långt. Rita först en vertikal linje som delar upp arbetsområdet i 2 områden, sedan en kortare linje nära toppen av det högra området, dela upp det i en mindre övre del och en större del under. Dela sedan upp talet i talpar, med början från decimalkomma. Enligt denna regel blir 79520789182.47897 lika med "7 95 20 78 91 82,47 89 70". Skriv detta nummer i det övre vänstra området.
- Som ett exempel, låt oss beräkna kvadratroten av 780,14. Dela upp din arbetsyta enligt ovan och skriv ner "7 80, 14" i det övre vänstra hörnet. Det är okej om det bara finns ett nummer längst till vänster, istället för två. Du skriver sedan svaret (kvadratroten av 780,14) överst i det högra området.

2. Hitta det största heltal n vars kvadrat är mindre än eller lika med siffran eller talet längst till vänster. Hitta den största kvadraten som är mindre än eller lika med detta tal, och ta sedan kvadratroten av denna kvadrat. Detta nummer är n. Observera att i det övre högra området och skriv kvadraten på n i den nedre kvadranten av det området.

3. Subtrahera talet du beräknade av siffran eller numret längst till vänster. Precis som med lång division är nästa steg att subtrahera kvadraten från talet som vi precis använde för att beräkna. Skriv detta tal under talet längst till vänster och subtrahera dem från varandra. Skriv svaret nedan.

4. Flytta nästa nummer nedåt. Placera detta bredvid värdet du hittade i föregående redigering. Multiplicera talet längst upp till höger med två och skriv ner det längst ner till höger. Spara utrymme bredvid talet du precis skrev ner för multiplikationssumman som du ska göra i nästa steg. Skriv här `"_×_="`.

5. Ange siffrorna till höger. I det tomma utrymmet av summan (till höger), skriv in det största heltal som kommer att göra resultatet av multiplikationssumman till höger mindre än eller lika med det aktuella talet till vänster.

6. Subtrahera talet du just beräknade från det aktuella talet till vänster. Så du subtraherar resultatet av multiplikationen till höger från det aktuella svaret till vänster. Skriv ditt svar direkt nedan.

7. Upprepa steg 4. Flytta nästa nummerpar från 780,14 nedåt. Om du kommer fram till ett kommatecken, skriv det kommatecken i svaret till höger. Multiplicera sedan talet längst upp till höger med 2 och skriv svaret bredvid ("_ × _") som ovan.

8. Upprepa steg 5 och 6. Hitta det största talet som ger ett svar som är mindre än eller lika med det aktuella talet till vänster. Lösa.

9. För att göra resultatet korrekt, upprepa föregående procedur tills du hittar svaret med antalet decimaler (hundradelar, tusendelar) du behöver.
Förstå proceduren
- Observera att om du dividerar 88962 med 7 med långdivision är det första steget detsamma: du har att göra med den första siffran i 88962 (8) och du vill att den största siffran multiplicerad med 7 ska vara mindre än eller lika med 8. I huvudsak bestämmer du d så att 7×d ≤ 8 < 7×(d+1). I detta fall är d lika med 1.
- I vårt exempel (10A+B)² = L = S = 100A² + 2×10A×B + B². Kom ihåg att 10A+B representerar vårt svar L tillsammans med B i enhetspositionen och A i tiotalspositionen. Till exempel, om A=1 och B=2 är 10A+B talet 12. (10A+B)² är arean av hela torget, medan 100A² är området för det största inre torget, B² är arean av minsta kvadraten och 10A×B är arean av var och en av de återstående rektanglarna. Genom denna långa, komplicerade procedur kan vi hitta arean av hela torget genom att lägga till arean av kvadraterna och rektanglarna som utgör den.

1. Betrakta talet vars kvadratrot du vill beräkna som arean S av en kvadrat. Eftersom arean av en kvadrat är L, där L är längden på en av dess sidor, så genom att ta kvadratroten av ditt tal, försöker du beräkna längden L på sidan av den kvadraten.

2. Ge varje siffra i ditt svar en bokstav. Ge variabeln A som den första siffran i L (kvadratroten vi försöker beräkna). B är den andra siffran, C är den tredje och så vidare.

3. Ge ett brev till var och en "nummerpar" av numret du börjar med. Ge variabeln Sa till det första siffrorna i S (startvärdet), Sb till det andra sifferparet osv.

4. Förstå sambandet mellan denna metod och lång division. Denna metod för att hitta en kvadratrot är i huvudsak lång division, dividering av det initiala värdet med dess kvadratrot och tar kvadratroten som svar "utgångspunkt". Precis som med lång division, där du bara är intresserad av nästa siffra åt gången, är du bara intresserad av de två nästa siffrorna åt gången (som motsvarar nästa siffra i kvadratroten).

5. Hitta det största talet vars kvadrat är mindre än eller lika med Sa är. Den första siffran A i vårt svar är då det största heltal vars kvadrat inte är större än Sa (A så att A² ≤ Sa < (A+1)²). I vårt exempel är Sa = 7 och 2² ≤ 7 < 3², så A = 2.

6. Visualisera kvadraten du vill hitta arean på. Ditt svar, kvadratroten av det initiala värdet, är L, som beskriver längden på en kvadrat av area S (startvärdet). Värdena för A, B och C representerar siffrorna i värdet L. Ett annat sätt att säga detta är att för ett 2-siffrigt svar, 10A + B = L, och för ett 3-siffrigt svar, 100A +10B + C = L, och så vidare.

7. Subtrahera A² från Sa. Ta med ett par siffror (Sb) ner från siffran S. sa sb är nästan den totala arean av kvadraten, från vilken du precis subtraherade arean av den största inre kvadraten. Resten är säg talet N1, som vi fick i steg 4 (N1 =380 i vårt exempel). N1 är lika med 2×10A×B + B² (arean av de 2 rektanglarna plus arean av den lilla kvadraten).

8. Titta på N1 = 2×10A×B + B², även skrivet som N1 = (2×10A + B) × B. I vårt exempel känner du redan till N1 (380) och A (2), så nu måste du hitta B. B är förmodligen inte ett heltal, så du behöver faktiskt hitta det största heltal B, så att (2×10A + B) × B ≤ N1. Så nu har du: N1 < (2×10A + (B+1)) × (B+1).)

9. Lös ekvationen. För att lösa denna ekvation, multiplicera A med 2, flytta den till tiotal (multiplicera med 10), placera B i enheterna och multiplicera resultatet med B. Med andra ord, (2×10A + B) × B. Det är precis vad du gör när du skriver "N_×_=" (med N=2×A) i den nedre högra kvadranten i steg 4. I steg 5 bestämmer du det största heltal B som passar under linjen, så att (2×10A + B) × B ≤ N1.

10. Subtrahera arean (2×10A + B) × B från den totala arean. Detta ger arean S-(10A+B)² som du ännu inte har tagit hänsyn till (och som du använder för att beräkna följande tal på samma sätt).

11. För att beräkna nästa siffra C, upprepa proceduren. Flytta nästa nummerpar från S nedåt (Sc) för att få N2 till vänster, och leta efter det största C så att du nu har: (2×10×(10A+B)+C) × C ≤ N2 (lika med två gånger det tvåsiffriga talet "A B" följd av "_×_=" . Bestäm nu det största antalet du kan ange här, vilket ger dig ett svar som är mindre än eller lika med N2.
Tips
- Flytta decimalkomma två platser (en faktor 100) flyttar decimalkomma i motsvarande kvadratrot med en plats (en faktor 10).
- I exemplet kan 1,73 betraktas som "resten": 780,14 = 27,9² + 1,73.
- Den här metoden fungerar för alla talsystem, inte bara decimalsystemet (tio decimaler).
- Lägg gärna beräkningarna där du vill. Vissa människor skriver det ovanför talet de vill beräkna kvadratroten ur.
- En alternativ metod är följande: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x) + ...))). Till exempel, för att beräkna kvadratroten av 780,14, skulle du ta heltal i kvadrat närmast 780,14 (28), så =780,14, x=28 och y=-3,86. Att fylla i och uppskatta ger oss x + y/(2x) och detta ger (förenklade termer) 78207/2800 eller cirka 27 931(1); nästa termin, 4374188/156607 eller cirka 27.930986(5). Varje term lägger till ungefär 3 decimaler med precision till den föregående.
Varningar
- Se till att du delar upp talet i par med början från decimalkomma. Dela 79520789182.47897 som "79 52 07 89 18 2.4 78 97" ger ett resultat som inte är korrekt.
"Beräkna kvadratroten ur ett tal utan miniräknare"
Оцените, пожалуйста статью