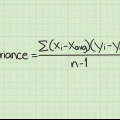Anta i det här fallet att du arbetar med medicinska data och att du har en lista över kroppstemperaturerna för tio patienter. Den förväntade normala kroppstemperaturen är 98,6 grader. Temperaturen på tio patienter mäts och ger värdena 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2 och 99.1. Temperaturen på tio patienter mäts och ger värdena 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2 och 99.1. Skriv dessa värden i den första kolumnen. 
Medelvärdet för en datamängd är summan av dess värden dividerat med antalet värden i uppsättningen. Detta kan representeras symboliskt, med variabeln  :
: 
För dessa data beräknas genomsnittet enligt följande: 



För den givna datamängden, subtrahera medelvärdet, 98,87, från varje uppmätt värde och fyll i den andra kolumnen med resultaten. Dessa tio beräkningar ser ut så här: 










För varje värde i den mellersta kolumnen, använd en miniräknare för att beräkna kvadraten. Anteckna resultaten i den tredje kolumnen, enligt följande: 










För denna datauppsättning beräknas SSE genom att lägga till de tio värdena i den tredje kolumnen: 



=Average(A2:___) Skriv inte tomt utrymme. Fyll i det utrymmet med cellnamnet för din senaste datapunkt. Till exempel, om du har 100 datapunkter, skulle du använda funktionen: =Average(A2:A101) Den här funktionen innehåller data från cellerna A2 till A101, eftersom den översta raden innehåller kolumnrubrikerna. När du trycker på Enter eller klickar till en annan cell i tabellen, fylls den nyligen programmerade cellen automatiskt med medelvärdet av dina datavärden. 
Felberäkningsfunktionen, som du anger i cell B2, är: =A2-$104$. Dollartecken behövs för att se till att du låser låda A104 för varje beräkning. 
I cell C2 anger du följande funktion: =B2^2 
Förutsatt att du har 100 datapunkter i tabellen, dra musen till cellerna B101 och C101. När du släpper musknappen kopieras formlerna till alla celler i tabellen. Tabellen ska automatiskt fyllas med de beräknade värdena. 
I en cell under tabellen, förmodligen C102 i det här exemplet, anger du följande funktion: =Summa(C2:C101) Om du klickar på Enter eller klickar bort i en annan cell i tabellen får du SSE-värdet för dina data. 

Därför, efter att du har beräknat SSE, kan du hitta standardavvikelsen enligt följande: 
För provet av temperaturmätningarna kan du hitta standardavvikelsen enligt följande: 




Beräkningarna för kovarians är för detaljerade för att beskrivas här, förutom att notera att du kommer att använda SSE för varje datatyp och sedan jämföra den. För en mer detaljerad beskrivning av kovariansen och de involverade beräkningarna, se hitta artiklar om detta ämne på wikiHow. Som ett exempel på att använda kovarians kan du jämföra patienternas ålder i en medicinsk studie med effektiviteten av ett läkemedel för att sänka febertemperaturen. Sedan har du en datauppsättning med åldrar och en andra datauppsättning med temperaturer. Du hittar sedan SSE för varje datamängd, och därifrån variansen, standardavvikelserna och kovariansen.
Beräkna summan av kvadrater (sse)
Summan av kvadrater, eller SSE, är en preliminär statistisk beräkning som leder till olika datavärden. När du har en uppsättning datavärden är det användbart att kunna avgöra hur nära dessa värden är relaterade till varandra. Du måste organisera dina data i en tabell och sedan göra några ganska enkla beräkningar. När du har hittat SSE för en datauppsättning kan du sedan hitta variansen och standardavvikelsen.
Steg
Metod 1 av 3: Beräkna SSE för hand

1. Gör en tabell med tre kolumner. Det enklaste sättet att beräkna SSE är att börja med en tabell med tre kolumner. Märk de tre kolumnerna  ,
,  , och
, och  .
.
 ,
,  , och
, och  .
.
2. Fyll i detaljerna. Den första kolumnen innehåller värdena för dina mätningar. Fyll kolumnen  med dina avläsningar. Detta kan vara resultatet av ett experiment, en statistisk studie eller bara data från ett matematiskt problem.
med dina avläsningar. Detta kan vara resultatet av ett experiment, en statistisk studie eller bara data från ett matematiskt problem.
 med dina avläsningar. Detta kan vara resultatet av ett experiment, en statistisk studie eller bara data från ett matematiskt problem.
med dina avläsningar. Detta kan vara resultatet av ett experiment, en statistisk studie eller bara data från ett matematiskt problem.
3. Beräkna medelvärdet. Innan du kan beräkna felet för varje mätning måste du beräkna medelvärdet av hela datamängden.
 :
:




4. Beräkna de individuella felvärdena. I den andra kolumnen i din tabell måste du ange felvärdena för varje datavärde. Felet är skillnaden mellan avläsningen och medelvärdet.











5. Beräkna SSE. I den tredje kolumnen i tabellen, hitta kvadraten på vart och ett av de resulterande värdena i den mellersta kolumnen. Dessa representerar kvadraterna på avvikelsen från medelvärdet för varje uppmätt datavärde.











6. Lägg ihop kvadraterna av felen. Det sista steget är att hitta summan av värdena i den tredje kolumnen. Det önskade resultatet är SSE, eller summan av kvadraterna av felen.

Metod 2 av 3: Skapa ett Excel-kalkylblad för att beräkna SSE

1. Märk kolumnerna i kalkylarket. Du skapar en tabell med tre kolumner i Excel, med samma tre rubriker som ovan.
- I cell A1, skriv "Värde" som rubrik.
- I ruta B1, skriv `Avvikelse` som rubrik.
- I ruta C1, skriv `Avvikelse i kvadrat` som rubrik.

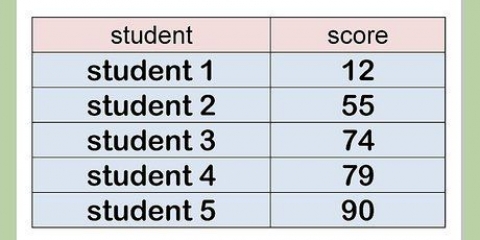
2. Ange dina uppgifter. I den första kolumnen måste du ange värdena för dina mätningar. Om setet är litet kan du enkelt skriva in det för hand. Om du har en stor datauppsättning kan du behöva kopiera och klistra in data i kolumnen.

3. Bestäm medelvärdet av datapunkterna. Excel har en funktion som räknar ut medelvärdet åt dig. I en tom cell under din datatabell (det spelar ingen roll vilken cell du väljer), skriv in:

4. Gå in i felmätningsfunktionen. I den första tomma cellen i kolumnen `Avvikelse` måste du ange en funktion för att beräkna skillnaden mellan varje datapunkt och medelvärdet. För att göra detta, använd cellnamnet där medelvärdet finns. Låt oss anta att du har använt cell A104 för nu.

5. Fyll i funktionen för de kvadratiska felen. I den tredje kolumnen kan du instruera Excel att beräkna önskad kvadrat.

6. Kopiera funktionerna för att fylla hela tabellen. Efter att ha angett funktionerna i den översta cellen i varje kolumn, B2 respektive C2, måste du fylla hela tabellen. Du kan skriva om funktionen i varje rad i tabellen, men det skulle ta alldeles för lång tid. Använd musen och markera cellerna B2 och C2 tillsammans och dra till den nedre cellen i varje kolumn utan att släppa musknappen.

7. Hitta SSE. Kolumn C i din tabell innehåller alla kvadratiska felvärden. Det sista steget är att låta Excel beräkna summan av dessa värden.
Metod 3 av 3: Relaterar SSE till andra statistiska data

1. Beräkna avvikelsen för SSE. Att hitta SSE för en datauppsättning är i allmänhet en byggsten för att hitta andra, mer användbara, värden. Den första av dessa är varians. Variansen är ett mått som anger hur mycket de uppmätta data avviker från medelvärdet. Det är faktiskt medelvärdet av de kvadratiska skillnaderna från medelvärdet. För provproblemet med patienternas temperatur kan vi anta att 10 patienter utgör endast ett prov. Därför beräknas variansen enligt följande: 


- Eftersom SSE är summan av de kvadratiska felen kan du hitta medelvärdet (det är variansen) bara genom att dividera med antalet värden. Men om du beräknar variansen för en urvalsuppsättning, snarare än en hel population, dividerar du variansen med (n-1) istället för n. Så:
- Varians = SSE/n, om du beräknar variansen för en hel population.
- Varians = SSE/(n-1), om du beräknar variansen för ett urval av data.




2. Beräkna standardavvikelsen för SSE. Standardavvikelsen är ett vanligt förekommande värde som anger hur mycket värdena för en datamängd avviker från medelvärdet. Standardavvikelsen är kvadratroten av variansen. Observera att variansen är medelvärdet av de kvadratiska felmåtten.






3. Använd SSE för att bestämma kovariansen. Den här artikeln fokuserade på datauppsättningar som bara mäter ett enstaka värde åt gången. Men i många studier kanske du jämför två separata värden. Till exempel vill du veta hur dessa två värden relaterar till varandra, inte bara till genomsnittet av datamängden. Detta värde är kovariansen.
"Beräkna summan av kvadrater (sse)"
Оцените, пожалуйста статью