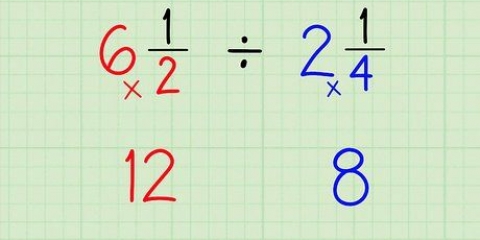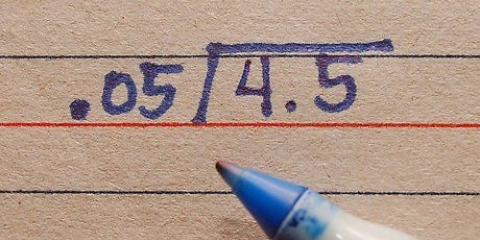Dela matriser

Om du vet hur man multiplicerar två matriser med varandra, då är du på god väg att kunna `dela` en matris med en annan matris. Division står inom citattecken eftersom matriser inte tekniskt kan delas. Istället multiplicerar vi en matris med omvänd från en annan matris. Dessa beräkningar används ofta för att lösa linjära ekvationssystem.

Steg

Del 1 av 3: Förstå att "delning" är omöjligt

Bild med titeln Dela matriser Steg 1
1. Förstå vad "dela" en matris innebär. Tekniskt sett finns det inget som heter matrisdelning. Att dela matriser är inte en definierad funktion. Det som ligger närmast det är att multiplicera med inversen av en annan matris. Med andra ord, även om [A] ÷ [B] inte är definierad, kan du lösa problemet [A] * [B]. Eftersom dessa två ekvationer är ekvivalenta med skalärer, "känns" detta som en matrisdivision, men det är viktigt att använda rätt terminologi.
  • Observera att [A] * [B] och [B] * [A] inte är samma problem. Du kanske måste lösa båda för att hitta alla möjliga svar.
  • Till exempel istället för (13263913)÷(7423){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}, skriva (13263913)*(7423)-1{displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{-1}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}.
    kanske du också borde (7423)-1*(13263913){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}^{-1}*{begin{pmatrix}13&26\39&13end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}*{begin{pmatrix}13&26\39&13end{pmatrix}} beräkna, vilket kan ge bara ett annat svar.
Bild med titeln Dela matriser Steg 2
2. Kontrollera att `divisormatrisen` är kvadratisk. För att kunna bestämma inversen av en matris måste den vara en kvadratisk matris, alltså med samma antal rader och kolumner. Om matrisen du vill hitta inversen av inte är en kvadratisk matris, så finns det ingen unik lösning på problemet.
  • Begreppet `divisormatris` är lite löst, eftersom det egentligen inte handlar om ett divisionsproblem. För [A] * [B] hänvisar detta till matris [B]. I vårt exempel är detta (7423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}}.
  • En matris med en invers kallas `invertibel` eller `icke singular.` Matriser utan invers är `singular.`
    • Bild med titeln Dela matriser Steg 3
    3. Kontrollera om de två matriserna kan multipliceras med varandra. För att multiplicera två matriser tillsammans måste antalet kolumner i den första matrisen vara lika med antalet rader i den andra matrisen. Om detta inte fungerar i båda fallen ([A] * [B] eller [B] * [A]) finns det ingen lösning på problemet.
  • Till exempel, om [A] är en 4 x 3 matris (4 rader, 3 kolumner) och [B] är en 2 x 2 matris (2 rader, 2 kolumner), så finns det ingen lösning. [A] * [B] fungerar inte eftersom 3 ≠ 2, och [B] * [A] fungerar inte eftersom 2 ≠ 4.
  • Vet att inversen [B] alltid har samma antal rader och kolumner som den ursprungliga matrisen [B]. Det är inte nödvändigt att beräkna inversen för att slutföra detta steg.
  • I vårt exempelproblem är båda matriserna 2 x 2, så de kan multipliceras i valfri ordning.
    • Bild med titeln Dela matriser Steg 4
    4. Bestäm determinanten för en 2 x 2 matris. Det krävs ytterligare en kontroll innan du kan bestämma inversen av en matris. Matrisens determinant kan inte vara noll. Om determinanten är noll, har matrisen ingen invers. Så här bestämmer du determinanten i det enklaste fallet (2 x 2-matrisen):
  • 2×2 matris: matrisens determinant (abcd){displaystyle {begin{pmatrix}a&före Kristus&dend{pmatrix}}}{begin{pmatrix}a&b\c&dend{pmatrix}} är ad - f.Kr. Med andra ord, ta produkten av huvuddiagonalen (upptill vänster till nedre höger), subtrahera sedan produkten av antidiagonalen (upptill höger till nedre vänster) därifrån.
  • Till exempel matrisen (7423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}} har determinanten (7)(3) - (4)(2) = 21 - 8 = 13. Detta är inte noll, så det är möjligt att bestämma inversen.
    • Bild med titeln Dela matriser Steg 5
    5. Bestäm determinanten för en större matris. Om din matris är 3 x 3 eller större, krävs lite mer arbete för att bestämma determinanten:
  • 3 x 3 matris: Välj ett element och korsa raden och kolumnen det tillhör. Bestäm determinanten för den återstående 2 x 2-matrisen, multiplicera med det valda elementet och behåll en matristeckentabell för att bestämma tecknet. Upprepa för de andra två elementen i samma rad och kolumn som den första du valde, lägg sedan till alla tre bestämningsfaktorerna. Läs den här artikeln för steg-för-steg-instruktioner och tips för att göra detta snabbare.
  • Större matriser: Användning av en grafräknare eller programvara rekommenderas här. Metoden liknar den för en 3 x 3 matris, men tar mycket tid om du gör detta för hand. Till exempel, för att hitta determinanten för en 4 x 4 matris måste du först hitta determinanterna för fyra 3 x 3 matriser.
    • Bild med titeln Dela matriser Steg 6
    6. Fortsätta. Om din matris inte är en kvadrat, eller om dess determinant är noll, skriv den som "ingen unik lösning". Problemet är löst. Om matrisen är en kvadrat och dess determinant inte är noll, hoppa till nästa del för nästa steg: hitta inversen.

    Del 2 av 3: Invertering av matrisen

    Bild med titeln Dela matriser Steg 7
    1. Byt positioner för elementen i huvuddiagonalen 2 x 2. Om du har att göra med en 2 x 2 matris kan du använda en genväg för att göra denna beräkning mycket enklare. Det första steget i denna snabba lösning innebär att byta det övre vänstra elementet med det nedre högra elementet. Till exempel:
    • (7423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}} → (3427){displaystyle {begin{pmatrix}3&4\2&7end{pmatrix}}}{begin{pmatrix}3&4\2&7end{pmatrix}}
    • Anmärkning: De flesta använder en miniräknare för att bestämma inversen av en 3 x 3-matris (eller större). Om du ändå vill räkna ut detta för hand, titta i slutet av denna del.
    Bild med titeln Dela matriser Steg 8
    2. Ta motsatsen till de andra två elementen men lämna dem i den positionen. Med andra ord, multiplicera toppen bedöma och botten vänster-element med-1:
  • (3427){displaystyle {begin{pmatrix}3&4\2&7end{pmatrix}}}{begin{pmatrix}3&4\2&7end{pmatrix}} → (3-4-27){displaystyle {begin{pmatrix}3&-4\-2&7end{pmatrix}}}{begin{pmatrix}3&-4\-2&7end{pmatrix}}
    • Bild med titeln Dela matriser Steg 9
    3. Ta det reciproka av determinanten. Du har hittat determinanten för denna matris i avsnittet ovan, så det finns ingen anledning att beräkna den igen. Skriv bara det reciproka av 1/(determinant):
  • I vårt exempel är determinanten 13. Det ömsesidiga i detta är 113{displaystyle {frac {1}{13}}}{frac{1}{13}}.
    • Bild med titeln Dela matriser Steg 10
    4. Multiplicera den nya matrisen med den reciproka av determinanten. Multiplicera varje element i den nya matrisen med det ömsesidiga du just hittat. Den resulterande matrisen är inversen av 2 x 2-matrisen:
  • 113*(3-4-27){displaystyle {frac {1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}}{frac{1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}
    =(313-413-213713){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}
    • Bild med titeln Dela matriser Steg 11
    5. Bekräfta att inversen är korrekt. För att kontrollera ditt arbete, multiplicera inversen med den ursprungliga matrisen. Om inversen är korrekt är deras produkt alltid matrisens identitet, (1001){displaystyle {begin{pmatrix}1&0\0&1end{pmatrix}}}{begin{pmatrix}1&0\0&1end{pmatrix}} Om det är matematiskt korrekt, fortsätt till nästa avsnitt för att slutföra problemutvecklingen.
  • För syftet med exempelproblemet multiplicerar vi (313-413-213713)*(7423)=(1001){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix }}.
  • Se wikihow för mer information om att multiplicera matriser.
  • Obs: Matrismultiplikation är inte kommutativ: ordningen på faktorerna har betydelse. När man multiplicerar en matris med dess invers, kommer båda att resultera i identitetsmatrisen.
    • Bild med titeln Dela matriser Steg 12
    6.Bestäm matrisinversionen av en 3 x 3-matris eller större. Om du inte är ny på denna process kan du spara mycket tid genom att använda en grafräknare eller matematisk programvara på större matriser. Om du behöver beräkna det för hand, här är en snabb sammanfattning av en metod du kan använda:
  • Lägg till identitetsmatrisen I till höger om din matris. Till exempel, [B] → [B | jag]. Identitetsmatrisen har `1`-element längs huvuddiagonalen och `0`-element i alla andra positioner.
  • Gör radoperationer för att reducera matrisen tills den vänstra sidan är i form av radnivå, fortsätt sedan att minska tills den vänstra sidan är identitetsmatrisen.
  • När hela operationen är klar är din matris i formen [I | B]. Med andra ord, den högra sidan blir inversen av den ursprungliga matrisen.

    • Del 3 av 3: Multiplicera matriserna för att slutföra problemet

    Bild med titeln Dela matriser Steg 13
    1. Skriv ner båda möjliga ekvationerna. I "vanlig matematik" med skalärer är multiplikation kommutativ; 2 x 6 = 6 x 2. Detta gäller inte matriser, så du kan behöva lösa två problem:
    • [A] * [B] är lösningen X för problem X[B] = [A].
    • [B] * [A] är lösningen X för problem [B]X = [A].
    • Om detta är en del av en ekvation, se till att du tillämpar samma operation på båda sidor av ekvationen. Om [A] = [C], så är [B][A] det inte lika med [C][B], eftersom [B] är till vänster om [A], men till höger om [C].
    Bild med titeln Dela matriser Steg 14
    2. Bestäm måtten på ditt svar. Dimensionerna för den slutliga matrisen är de yttre dimensionerna av de två faktorerna. Den har samma antal rader som den första matrisen och samma antal kolumner som den andra matrisen.
  • För att återgå till det ursprungliga exemplet: båda (13263913){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}} och (313-413-213713){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}} är 2 x 2 matriser, så måtten på svaret är också 2 x 2.
  • För att ta ett lite mer komplicerat exempel: om [A] är en 4 x är en 3-matris och [B] är en 3 x 3 matris, då har matrisen [A] * [B] måtten 4 x 3.
    • Bild med titeln Dela matriser Steg 15
    3. Bestäm värdet på det första elementet. Kolla in den länkade artikeln för detaljerade instruktioner, eller uppdatera dina kunskaper med denna sammanfattning:
  • För att hitta rad 1, kolumn 1 i [A][B], hitta punktprodukten för [A] rad 1 och [B] kolumn 1. Så, för en 2 x 2 matris, räknar du a1,1*b1,1+a1,2*b2,1{displaystyle a_{1,1}*b_{1,1}+a_{1,2}*b_{2,1}}a_{{1,1}}*b_{{1,1}}+a_{{1,2}}*b_{{2,1}}.
  • I vårt exempel (13263913)*(313-413-213713){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}, är rad 1 kolumn 1 i ditt svar:
    (13*313)+(26*-213){displaystyle (13*{frac {3}{13}})+(26*{frac {-2}{13}})}(13*{frac{3}{13}})+(26*{frac{-2}{13}})
    =3+-4{displaystyle =3+-4}=3+-4
    =-1{displaystyle =-1}=-1
    • Bild med titeln Dela matriser Steg 16
    4. Beräkna prickprodukten för varje position i din matris. Till exempel är elementet i position 2.1 punktprodukten av [A] rad 2 och [B] kolumn 1. Försök att räkna ut exemplet själv. Du bör få följande svar:
  • (13263913)*(313-413-213713)=(-1107-5){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end {pmatrix}}
  • Och den andra lösningen: (313-413-213713)*(13263913)=(-92193){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{ pmmatrix}}

    • Tips

    • Du kan dividera en matris med en skalär, genom att dividera varje element i matrisen med skalären.
    • Till exempel matrisen (6824){displaystyle {begin{pmatrix}6&8\2&4end{pmatrix}}}{begin{pmatrix}6&8\2&4end{pmatrix}} dividerat med 2 = (3412){displaystyle {begin{pmatrix}3&4\1&2end{pmatrix}}}{begin{pmatrix}3&4\1&2end{pmatrix}}

    Varningar

    • Miniräknare är inte alltid 100% korrekta i matrismatte. Till exempel, om din miniräknare indikerar att ett element har ett mycket litet värde (t.ex. 2E), så är värdet förmodligen noll.

    Shv.FaqCartx.info / Utbildning & kommunikation
    Оцените, пожалуйста статью
    Ansluter kindle till en tv
    Ansluter kindle till en tv
    Gör ett folioskop
    Gör ett folioskop
    Kontakta en säljare på amazon
    Kontakta en säljare på amazon
    Att förändra världen
    Att förändra världen
    Vet när laxen är tillräckligt tillagad
    Vet när laxen är tillräckligt tillagad
    Vara bra på sport
    Vara bra på sport