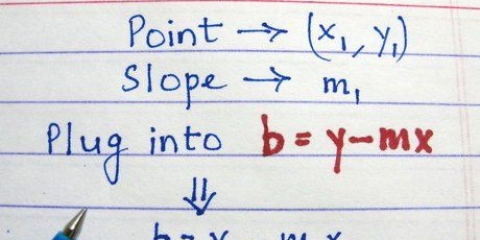Använda sluttningsformeln

Steg
Tips

Lutningsformeln är ett vanligt sätt att skriva en linjär ekvation. Denna formel är skriven som "y = mx + b" – där bokstäverna ges ett visst värde för att kunna lösa denna ekvation, eller där ekvationen löses för att hitta variablernas värden. Så: "X" och "y" är de "X-" och "y"-koordinater för en linje, "m" är lutningen (lutningen), förhållandet (ändring av y)/(ändring av x), och "b" är skärningspunkten med y-axeln. Om du vill veta hur du använder lutningsformeln har du kommit rätt.

Steg

Metod 1 av 5: Använd lutningsformeln för problem

1. Läs uppgiften. Innan du kan gå vidare måste du läsa uppgiften noggrant så att du förstår exakt vad som efterfrågas av dig. Läs följande uttalande: Ditt bankkonto ökar linjärt varje vecka. Om du har 560 USD på ditt bankkonto efter 20 veckors arbete och 585 USD efter 21 veckor, hur uttrycker du förhållandet mellan det belopp du tjänade och hur många veckor du arbetade med hjälp av lutningsformeln.

Bild med titeln Använd Slope Intercept Form (i Algebra) Steg 2

2. Tänk på problemet i termer av lutningsformeln. Du bör skriva ner det så här: y = mx + b. Variabeln "m" är lutningen och "b" är startpunkten där linjen skär y-axeln. Observera att problemet säger det, " Ditt bankkonto ökar linjärt varje vecka," vilket innebär att du sparar lika mycket varje vecka, vilket i sin tur gör att du har en rak, lutande linje. Den där "konstant," och jämnt kontinuerlig sparplan är det som gör den linjär. Om du inte sparar lika mycket varje gång är det inte linjärt.

Bild med titeln Använd Slope Intercept Form (i Algebra) Steg 3

3. Hitta lutningen på linjen. För att hitta lutningen måste du kunna bestämma förändringshastigheten. Om du börjar med €560 och följande vecka har du €585, då har du tjänat €25 efter 1 veckas arbete. Du kan också beräkna detta genom att subtrahera €560 från €585. 585-560 = 25.

4. Hitta skärningspunkten med y-axeln. För att hitta denna korsning, även kallad "b" i y = mx + b måste du veta startpunkten för ditt problem (det vill säga skärningspunkten med y-axeln). Det betyder att du måste ta reda på hur mycket pengar du började med. Om du hade 560 USD efter 20 veckors arbete och du vet att du tjänade 25 USD på en vecka, använd följande multiplikation för att beräkna hur mycket du tjänade på 20 veckor. 20 x 25 = 500, så du tjänade 500 USD under dessa veckor.

För efter 20 veckor har du €560 och dessutom tjänat €500. då vet du hur mycket du började med att subtrahera 500 från 560. 560 - 500 = 60.

Så den "b" eller startpunkten är 60.

5. Skriv ekvationen. Nu när du vet lutningen, m är 25, (tjänar 25 dollar per vecka), och startpunkten b är 60, kan du koppla in detta i ekvationen:

y = mx + b

y = 25x + 60

6. Testa om ekvationen är korrekt. De "y" är summan pengar du har tjänat och "X" antalet veckor du har arbetat. Se hur mycket pengar du har tjänat under ett givet antal veckor genom att ange denna data i ekvationen. Prova två exempel:

Hur mycket tjänade du på 10 veckor? fylla "10" in för "X" att ta reda på här.

y = 25x + 60 =

y = 25(10) + 60 =

y = 250 + 60 =

y = 310. Efter 10 veckor har du tjänat 310 €.

Hur många veckor måste du arbeta för att tjäna 800 euro? fylla "800" in för "y"-variabel i ekvationen att komma bakom värdet på "X" att komma.

y = 25x + 60 =

800 = 25x + 60 =

800 - 60 =

25x = 740 =

25x/25 = 740/25 =

x = 29.6. Du kan tjäna 800 euro på cirka 30 veckor.

Metod 2 av 5: Konvertera en ekvation till lutningsformeln

1. Skriv ekvationen. Anta att du har att göra med följande ekvation, 4y +3x = 16.

2. Isolera y-termen på ena sidan av ekvationen. Det gör du genom att subtrahera 3x från båda sidor av ekvationen. Ekvationen ska nu se ut så här: 4y = -3x +16.

4y + 3x = 16

4y + 3x - 3x = 16 -3x

4y = -3x +16

3. Dividera alla termer med koefficienten y. Detta är numret för variabeln y. Lägg inte en siffra här, då är du klar. Om det finns ett tal (koefficienten), dividera varje term i ekvationen med det talet. I det här fallet är y-koefficienten 4, så du måste dividera 4x, -3x och 16 med 4 för att få det slutliga svaret. Så här fungerar det här:

4y = -3x +16 =

/₄y = /₄X +/_{4 = (genom division)}

y = /₄X + 4 (genom att förenkla divisionen)

4. Bestäm termerna i ekvationen. När du använder ekvationen för att dra en linje, kom ihåg det "y" y-koordinaten är en "-3/4" sluttningen eller sluttningen, "X" är då x-koordinaterna och "4" skärningen med y-axeln.

Metod 3 av 5: Lutningsformeln med hjälp av en punkt och lutningen

1. Skriv linjens ekvation som lutningsformeln. Skriv bara först y = mx + b. Du kan sedan fylla i ekvationen när du har tillräckligt med data. Anta att du vill lösa följande problem: Hitta ekvationen för en linje med lutningen 4 som går genom punkten (-1, -6).

2. Fyll i detaljerna. Du vet det "m" är lika med linjens lutning, lika med 4 och det "y" och "X" respektive "X" och "y" koordinaterna är. I det här fallet är uppgifterna "X" = -1 och "y" = -6. "b" representerar skärningen med y-axeln; detta värde är ännu inte känt. Så här ser ekvationen ut nu:

y = -6, m = 4, x = -1 (de angivna värdena)

y = mx + b (formeln)

-6 = (4)(-1) + b (efter ifyllning)

3. Lösa åt "b". Nu gäller det att träna "b," hitta skärningen med y-axeln. Multiplicera 4 och -1 och subtrahera sedan resultatet från -6. Så här gör du det:

-6 = (4)(-1) + b

-6 = -4 + b

-6 - (-4) = -4 -(-4) + b

-6 - (-4) = b (term förenklad höger)

-2 = b (term vänster förenklad)

4. Skriv ekvationen. Nu du "b," du kan fylla i de nödvändiga värdena i lutningsformeln. Allt du behöver veta är lutningen och skärningen med y-axeln (b):

m = 4, b = -2

y = mx + b

y = 4x -2 (substitution)

Metod 4 av 5: Skriv ner lutningsformeln med två punkter

1. Skriv ner de två punkterna. Innan du kan göra linjens ekvation skriver du först ner de två punkter som ges. Anta att du vill lösa följande problem: Hitta ekvationen för linjen genom punkterna (-2, 4) och (1, 2).

2. Använd dessa punkter för att hitta ekvationens lutning. Formeln för att bestämma linjens lutning genom två punkter är (y₂ - y₁) / (x₂ - X₁). Du har att göra med koordinaterna (x₁, Y₁) = (-2, 4) och (x₂, Y₂ ) = (1, 2). Infoga nu detta värde i ekvationen och lös m.

(y₂ - y₁) / (x₂ - X₁) =

(2 - 4)/(1 - -2) =

-2/3 = m

Linjens lutning är -2/3.

3. Välj en av punkterna att lösa för skärningspunkten med y-axeln. Det spelar ingen roll vilket par du väljer. Välj den som är lättast för dig att arbeta med Anta att du väljer punkten (1, 2). Fyll nu i detta i ekvationen "y = mx + b". Lösa åt "b":

y = 2, x, = 1, m = -2/3

y = mx + b

2 = (-2/3)(1) + b

2 = -2/3 + b

2 - (-2/3) = b

2 + 2/3 = b, eller b = /₃

4. Fyll i siffrorna i den ursprungliga ekvationen. Nu när du vet att lutningen är lika med 2/3 och skärningen med y-axeln ("b") är lika med 2 2/3, du kan koppla in dessa värden till den ursprungliga ekvationen på linjen och du är klar.

y = mx + b

y = /₃X + 2 2/3

Metod 5 av 5: Rita linjen

1. Skriv ekvationen och använd den för att dra linjen. Anta att du har följande ekvation: y = 4x + 3.

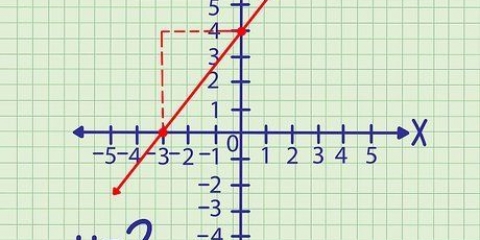
2. Börja med skärningspunkten med y-axeln. Skärningen med y-axeln ges av "+3" eller "b" i ekvationen. Detta är punkten (0, 3). Ange denna punkt med en prick.

3. Använd linjens lutning för att hitta koordinaterna för den andra punkten. För du vet att lutningen representeras av "m=4," kan man säga att lutningen är lika med y/x=4/1. Detta innebär att varje gång linjen stiger 4 punkter på y-axeln, skiftar den 1 punkt till höger på x-axeln. Så du börjar vid punkt (0, 3) och går upp 4 punkter och 1 punkt till höger, och slutar vid punkt (1, 7) som nästa punkt på linjen.

Om lutningen är negativ går linjen ner från vänster till höger.

4. Förbind de två punkterna med en linje. Använd en penna och linjal för detta. Detta är allt du behöver göra och du har ritat en perfekt linje enligt den givna ekvationen. Två poäng räcker för att dra gränsen. Kontrollera vid behov genom att rita några fler punkter.

Tips

Ett exempel på linjär minskning och ökning är den konstanta förändringen av ett objekts hastighet, mätt i meter per sekund, avstånd mätt över tid.
Algebra är aktiv. Du behöver inte bara läsa och förstå teorin, du måste också arbeta med den för att förstå hur den fungerar.
Detta är det riktiga sättet att visa att du förstår: Förändringen av y jämfört med förändringen av x kallas ökningen (tillväxt) eller minskning (försämring) av skillnaden mellan y dividerat med skillnaden mellan x. Att dividera med kallas också ett förhållande, bråk eller förhållande. Här är förhållandet "graden av förändring.
Träna i början också ut de enkla övningarna på papper. Om du arbetar med svårare övningar i ett senare skede kommer du att ha mycket nytta av denna metod eftersom den ger dig en bättre uppfattning om proceduren att följa för att göra en graf.
Kom ihåg: multiplikation kommer före addition, så y = mx + b; så först m ×x och sedan x+b.
Läs inte bara exemplen. Skriv ner dem och öva på de olika stegen så att du förstår hela processen väl.
Du kommer säkert att imponera på din lärare om du lär dig att förstå hur man tillämpar en linjär ekvation på alla typer av problem.
Det kartesiska koordinatsystemet som används i algebra för att göra en graf, etc. är uppkallad efter sin franska uppfinnare och använder den för koordinater på kartor. Liknande system används inom olika områden inom matematiken, såväl som inom astronomi, navigering, datorskärmar, neonskyltar och resultattavlor, eller för att lokalisera nästan vad som helst.
Lutningen på en linje mäter förhållandet mellan den vertikala förändringen (y) jämfört med den horisontella förändringen (x). Det kan handla om punkter på en linje, men också om en viss linjär tillväxthastighet, eller lutningen på en kulle.