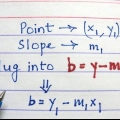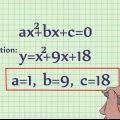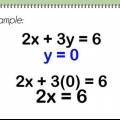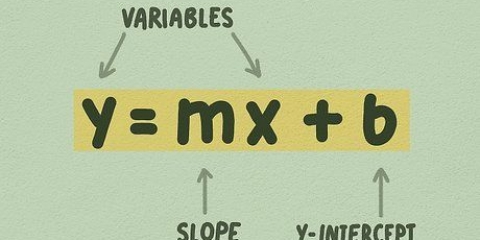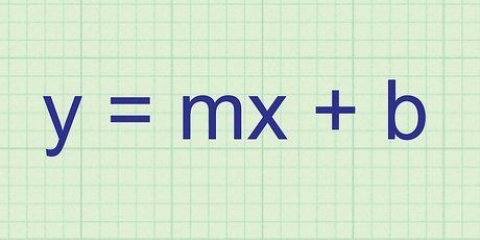Hitta skärningspunkten mellan en ekvation och Y-axeln

Steg
Tips

Y-snittet för en ekvation är den punkt där grafen för en ekvation skär y-axeln. Det finns flera sätt att hitta denna korsning, beroende på informationen som ges i början av ditt kommando.

Steg

Metod 1 av 3: Hitta skärningspunkten med y-axeln med hjälp av lutningen

1. Notera lutningen. Lutningen för `y över x` är ett enda tal som anger lutningen på en linje. Denna typ av problem ger dig också (x,y)-koordinaten för en punkt på grafen. Om du inte har båda dessa detaljer, fortsätt med de andra metoderna nedan.

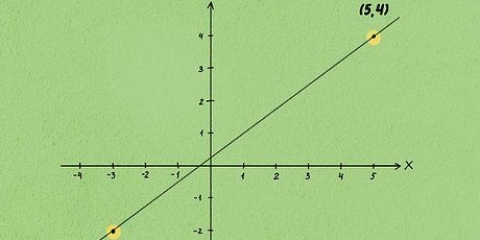
Exempel 1: En rak linje med lutning 2 går igenom punkten (-3,4). Bestäm skärningspunkten med y-axeln för denna linje med hjälp av stegen nedan.

Bild med titeln Hitta Y Intercept Steg 2

2. Lär dig den vanliga formen av en linjär ekvation. Vilken rät linje som helst kan skrivas som y = mx + b. När ekvationen är i denna form, är m lutningen och konstanten b skärningen med y-axeln.

Bild med titeln Hitta Y Intercept Steg 3

3. Ersätt lutningen i denna ekvation. Skriv ner den linjära ekvationen, men istället för m använder du lutningen på din lina.

Exempel 1 (fortsättning):y = mx + b
m = lutning = 2
y = 2x + b

Bild med titeln Hitta Y Intercept Steg 4

4. Ersätt x och y med punktens koordinater. Om du har koordinaterna för en punkt på linjen kan du X och y-ersätt koordinater för X och y i din linjära ekvation. Gör detta för att jämföra din uppgift.

Exempel 1 (fortsättning): Punkten (3,4) är på denna linje. vid denna tidpunkt, x = 3 och y = 4.
Byt ut dessa värden till y = 2X +b:
4 = 2(3) + b

Bild med titeln Hitta Y Intercept Steg 5

5. Lösa åt b. Glöm inte, b är skärningspunkten med linjens y-axel. Nu b är den enda variabeln i ekvationen, arrangera om ekvationen för att lösa denna variabel och hitta svaret.

Exempel 1 (fortsättning):4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
Skärningen av denna linje med y-axeln är -2.

Bild med titeln Hitta Y Intercept Steg 6

6. Skriv ner detta som en koordinat. Skärningen med y-axeln är den punkt där linjen skär y-axeln. Eftersom y-axeln går genom punkten x = 0 är x-koordinaten för skärningspunkten med y-axeln alltid 0.

Exempel 1 (fortsättning): Skärningen med y-axeln är vid y = -2, så koordinatpunkten är (0, -2).

Metod 2 av 3: Använd två punkter

Bild med titeln Hitta Y Intercept Steg 7

1. Notera koordinaterna för båda punkterna. Denna metod behandlar problem där endast två punkter ges på en rät linje. Skriv varje koordinat i formen (x,y).

Bild med titeln Hitta Y Intercept Steg 8

2. Exempel 2: En rät linje går genom punkterna (1, 2) och (3, -4). Bestäm skärningspunkten med y-axeln för denna linje med hjälp av stegen nedan.

Bild med titeln Hitta Y Intercept Steg 9

3. Beräkna x- och y-värdena. Lutningen eller lutningen är ett mått på hur mycket linjen rör sig i vertikal riktning för varje steg i horisontell riktning. Du kanske känner till detta som "y över x" (

\frac{y}{X}

${frac{y}{x}}$ ). Så här bestämmer du dessa värden med hjälp av två punkter:

Ändringen av `y` är förändringen i vertikal riktning, eller skillnaden mellan y-värden för de två punkterna.

Ändringen av `x` är ändringen i horisontell riktning, eller skillnaden mellan X-värden för de två punkterna.

Exempel 2 (fortsättning): Y-värdena för de två punkterna är 2 och -4, så linjen ökar i vertikal riktning med (-4) - (2) = -6.
X-värdena för de två punkterna (i samma ordning) är 1 och 3, så linjen ökar horisontellt med 3 - 1 = 2.

Bild med titeln Hitta Y Intercept Steg 10

4. Dividera y med x för att bestämma lutningen. Nu när du känner till dessa två värden kan du använda dem i `

\frac{y}{X}

${frac{y}{x}}$ ` för att bestämma linjens lutning.

Exempel 2 (fortsättning):

s l O sid e = \frac{y}{X} = - 6 2 =

$lutning={frac{y}{x}}={frac{-6}{2}}=$ -3.

Bild med titeln Hitta Y Intercept Steg 11

5. Ta en ny titt på standardformen för en linjär ekvation. Du kan beskriva en rak linje med formeln y = mx + b, varigenom m lutningen är och b skärningen med y-axeln. Nu när vi har lutningen m och en punkt (x,y), kan vi använda denna ekvation för att hitta b att lösa (skärningen med y-axeln).

Bild med titeln Hitta Y Intercept Steg 12

6. Fyll i lutningen och punkten i ekvationen. Ta ekvationen i standardform och ersätt m av lutningen du beräknat. Byt ut variablerna X och y med koordinaterna för en enda punkt på linjen. Det spelar ingen roll vilken punkt du använder.

Exempel 2 (fortsättning): y = mx + b
Lutning = m = -3, alltså y = -3x + b
Linjen går genom en punkt med (x,y)-koordinater (1,2), alltså 2 = -3(1) + b.

Bild med titeln Hitta Y Intercept Steg 13

7. Lös för b. Nu är den enda variabeln kvar i ekvationen b, skärningen med y-axeln. Ordna om ekvationen så att b på ena sidan av ekvationen, och du har ditt svar. Kom ihåg att skärningen med y-axeln alltid har en x-koordinat på 0.

Exempel 2 (fortsättning): 2 = -3(1) + b
2 = -3 + b
5 = b
Skärningen med y-axeln är (0,5).

Metod 3 av 3: Använd en ekvation

Bild med titeln Hitta Y Intercept Steg 14

1. Skriv ner linjens ekvation. Om du har linjens ekvation kan du bestämma skärningspunkten med y-axeln med en liten algebra.

Exempel 3: Vilken är skärningspunkten med linjens y-axel x + 4y = 16?
Notera: Exempel 3 är en rak linje. Se slutet av det här avsnittet för ett exempel på en andragradsekvation (med en variabel upphöjd till 2).

Bild med titeln Hitta Y Intercept Steg 15

2. Ersätt x med 0. Y-axeln är en vertikal linje genom x = 0. Detta betyder att varje punkt på y-axeln har en x-koordinat på 0, inklusive skärningspunkten mellan linjen och y-axeln. Ange 0 för x i ekvationen.

Exempel 3 (fortsättning): x + 4y = 16
x = 0
0 + 4y = 16
4y = 16

Bild med titeln Hitta Y Intercept Steg 16

3. Lös för y. Svaret är skärningspunkten mellan linjen och y-axeln.

Exempel 3 (fortsättning): 4y = 16

4 y 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
Skärningen av linjen med y-axeln är 4.

Bild med titeln Hitta Y Intercept Steg 17

4. Bekräfta detta genom att rita en graf (valfritt). Kontrollera ditt svar genom att rita ut ekvationen så exakt som möjligt. Den punkt där linjen går genom y-axeln är skärningspunkten med y-axeln.

Bild med titeln Hitta Y Intercept Steg 18

5. Hitta skärningspunkten med y-axeln för en andragradsekvation. En andragradsekvation har en variabel (x eller y) upphöjd till andra potens. Med samma substitution kan du lösa för y, men eftersom andragradsekvationen är en kurva kan den skära y-axeln vid 0, 1 eller 2 punkter. Det betyder att du kommer att få 0, 1 eller 2 svar.

Exempel 4: För att hitta skärningspunkten för

y 2 = X + 1

$y^{2}=x+1$ med y-axeln ersätter du x = 0 och lösa andragradsekvationen.
I det här fallet kan vi

y 2 = 0 + 1

$y^{2}=0+1$ lösa genom att ta kvadratroten på båda sidorna. Kom ihåg att du får två svar när du tar kvadratrot: ett negativt och ett positivt svar.

\sqrt{y} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 eller y = -1. Dessa är båda skärningspunkter med y-axeln för denna kurva.

Tips

Vissa länder använder en c eller någon annan variabel för b i ekvationen y = mx + b. Dess innebörd förblir dock densamma; det är bara en annan notation.
För mer komplicerade ekvationer kan du använda termerna med y isolera på ena sidan av ekvationen.
När du beräknar lutningen mellan två punkter kan du X och y-subtrahera koordinater i valfri ordning, så länge du sätter punkten i samma ordning för både y och x. Till exempel kan lutningen mellan (1, 12) och (3, 7) beräknas på två olika sätt:

Andra punkten – första punkten: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2,5$
Första punkten – andra punkten: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2,5$