Instrucțiuni gratuite pas cu pas 
Detta värde är x-värdet i din lutningsekvation, där lutning = y/x. Så om du mätte 7 kommer din ekvation att vara "lutning = y/7". 
Detta belopp är det motsatta eller y-värde i din lutningsekvation. Så om du mätte 5, blir ekvationen "lutning = 5/7". 
Så för att fortsätta exemplet blir ekvationen `lutning = 5/7` och det är 0,71428571. 
För att fortsätta med exemplet ger en lutning på 0,71428571 en vinkel på 35,5 grader. 
Du har faktiskt skapat en liten rät vinkel vid den trubbiga vinkeln du vill mäta, vilket gör den övre radien för den trubbiga vinkeln till hypotenusan för din räta vinkel. 
Du bestämmer lutningen på den spetsiga triangelns vinkel, med vilken du kan beräkna graderna i den spetsiga vinkeln. Summan av kardemumman är intilliggande värde i ekvationen `lutning = motsatt/intilliggande`. 
Längden på din vertikala linje är motsatt värde i ekvationen `lutning = motsatt/intilliggande`. Om du känner till värdena för både motsatt och intilliggande, kan du beräkna lutningen för den spetsiga vinkeln. 
Till exempel kommer ekvationen `lutning = 2/4` att ge en lutning på 0,5. 
För att fortsätta med exemplet, om din lutning är 0,5, är den spetsiga vinkeln en vinkel på 26,565 grader. 
För att fortsätta med exemplet, om du har en spetsig vinkel på 26,565 grader, har du en trubbig vinkel på 153,435 grader (180 – 26,565 = 153,435). 
Den horisontella linjen kommer att vara den intilliggande sidan av din triangel, och den vertikala linjen kommer att vara den motsatta sidan av den spetsiga vinkeln du vill mäta. 
Mät den horisontella linjen från spetsen till den punkt där den skär den vertikala linjen. Mät den vertikala linjen från den punkt där den skär den horisontella linjen till den punkt där den skär den diagonala linjen. 
Till exempel, om din horisontella linje är 8 och den vertikala linjen är 4, så blir din ekvation "lutning = 4/8". Lutningen på din vinkel är då 0,5. 
För att fortsätta med exemplet, om din lutning är 0,5, blir den spetsiga vinkeln 26,565 grader. 
För att fortsätta med exemplet, om den mindre spetsiga vinkeln är 26,565 grader, är reflexvinkeln 333,435 grader.
Mäta en vinkel utan gradskiva
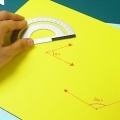
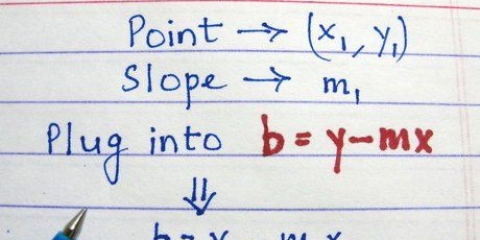Det enklaste sättet att mäta en vinkel är med a gradskiva. Men om du inte har en gradskiva till hands kan du bestämma storleken på en vinkel med hjälp av de grundläggande geometriska principerna för trianglar. Du behöver en vetenskaplig miniräknare för att lösa ekvationerna. De flesta smartphones är utrustade med det, men du kan också ladda ner gratisappar eller använda en gratis kalkylator online. Beräkningarna du måste göra beror på om du har att göra med en spetsig vinkel (mindre än 90 grader), trubbig vinkel (mer än 90 grader men mindre än 180) eller en "reflexvinkel" (mer än 180 grader men mindre) . än 360).
Steg
Metod 1 av 3: Skarpa hörn
1. Rita en vertikal linje som förbinder vinkelns två strålar. För att hitta antalet grader i en spetsig vinkel, koppla ihop de två strålarna för att bilda en triangel. Rikta in den korta änden av din linjal med den nedre strålen och rita sedan en vertikal linje som skär den andra strålen med hjälp av den långa sidan av din linjal.
- Den vertikala linjen skapar en rätvinklig triangel. Vinkeln som bildas av den intilliggande sidan (vinkelns nedre radie) av triangeln och den motsatta sidan (den vertikala linjen) är 90 grader.
2. Mät längden på den intilliggande sidan runt den intilliggande eller x-värde hitta. Placera änden av din linjal på vertexet. Mät längden på den intilliggande sidan från vertex till den punkt där den skär den motsatta sidan.
3. Vi mäter längden på den andra sidan för att hitta motsatsen. Rikta in den korta änden av din linjal med den intilliggande sidan av triangeln. Mät längden på den vertikala linjen från den punkt där den möter den intilliggande sidan till den punkt där den möter den övre radien av hörnet (hypotenusan i din triangel).
4. Dividera motsatsen med intilliggande (y-värdet med x-värdet) för att hitta lutningen på vinkeln. Lutningen är brantheten på den diagonala linjen, eller hypotenusan, i din triangel. När du vet detta nummer kan du beräkna graderna av din spetsiga vinkel.
Dricks: Avrunda inte talet innan du konverterar det här talet till grader - annars blir resultatet mindre exakt.
5. Använd din miniräknare för att beräkna vinkeln i grader. Skriv lutningsvärdet i din vetenskapliga miniräknare och tryck sedan på knappen för inverterad tangent (tan). Detta ger dig vinkeln i grader.
Metod 2 av 3: trubbig vinkel
1. Förläng den nedre radien av hörnet i en rak linje. Markera din vertex med en punkt, använd sedan långsidan av din linjal för att rita en rak linje till vänster om vertex. Den nedre radien av hörnet bör vara en enda lång linje som sträcker sig under hörnets öppna övre radie.
- Se till att linjen är helt rak. Om linjen är vinklad uppåt eller nedåt kommer det att förstöra noggrannheten i din ekvation.
Dricks: Om du arbetar på ofodrat papper kan du rikta in linjalens kortsida med sidan av papperet för att se till att linjeförlängningen är rak.
2. Rita en vertikal linje som förbinder den översta strålen med linjen. Rikta in den korta sidan av din linjal med den nedre strålen vid en punkt där långsidan skär den översta strålen. Följ långsidan för att dra en linje rakt upp från den nedre strålen som förbinder de två.
3. Mät längden på den nedre raden från vertex. Placera din linjal under den nedre raden, börja vid den vertikala linjen som skapar den rätta vinkeln. Mät längden från den skärningspunkten till spetsen av den ursprungliga vinkeln.
4. Mät längden på den vertikala linjen. Rikta in den korta änden av din linjal med den nedre raden av den lilla spetsiga triangeln. Mät med linjalen till den punkt där den vertikala linjen skär den öppna radien för din trubbiga vinkel. Detta är längden på din vertikala linje.
5. Bestäm lutningen för den spetsiga vinkeln. Dela motsatt värde av intilliggande värde för att bestämma lutningen för den spetsiga vinkeln. Du kommer att använda detta värde för att beräkna den spetsiga vinkeln i grader.
6. Beräkna graderna av den spetsiga vinkeln. Ange lutningen i din vetenskapliga miniräknare och tryck sedan på knappen `omvänd solbränna`. Värdet som visas är antalet grader av den spetsiga vinkeln.
7. Subtrahera antalet grader av den spetsiga vinkeln från 180. En platt linje är en rät vinkel med 180 grader. Eftersom du har ritat en rät linje blir summan av den spetsa vinkeln du beräknat och den trubbiga vinkeln 180 grader. Att subtrahera graderna av den spetsiga vinkeln från 180 ger dig antalet grader av din trubbiga vinkel.
Metod 3 av 3: Reflexvinkel (trubbig vinkel > 180)
1. Bestäm den mindre spetsiga vinkeln för den trubbiga vinkeln som är större än 180 grader (nedan: reflexvinkel). En reflexvinkel är större än 180 grader men mindre än 360 grader. Det betyder att om du tittar på reflexvinkeln kommer du också att se en spetsig vinkel inom den.
- Genom att bestämma antalet grader av den spetsiga vinkeln kan du beräkna antalet grader av reflexvinkeln. Du kan använda den grundläggande lutningsekvationen och den inversa tangentfunktionen på din vetenskapliga miniräknare för att hitta graderna av den spetsiga vinkeln.
Dricks: Om du är förvirrad eftersom vinkeln är upp och ner, vänd på papperet och ignorera reflexvinkeln tills det sista steget.
2. Rita en vertikal linje som förbinder strålarna i den spetsiga vinkeln. Rikta in den korta änden av din linjal med radien på hörnet som är horisontellt istället för diagonalt. Rita sedan en vertikal linje som korsar hörnets horisontella radie.
3. Mät motsatsen och den angränsande linjen för den spetsiga vinkeln. I ekvationen `lutning = motsatt/intilliggande` är motsatsen längden på den vertikala linjen, eller den motsatta sidan av din triangel. Intill är längden på den horisontella linjen, eller den intilliggande sidan av din triangel.
4. Dividera motsatsen med intilliggande för att beräkna den spetsiga vinkelns lutning. Använd värdena som finns för längden på de vertikala och horisontella linjerna i din lutningsekvation. När du delar längden på den vertikala linjen med längden på den horisontella linjen får du lutningen för vinkeln.
5. Använd din miniräknare för att hitta graderna av den spetsiga vinkeln. Skriv in värdet du har för vinkelns lutning i din vetenskapliga miniräknare och tryck sedan på knappen `invers tangent` (tan). Värdet som visas är antalet grader av den mindre, spetsiga vinkeln.
6. Subtrahera antalet grader av den spetsiga vinkeln från 360. En cirkel har 360 grader. Eftersom en reflexvinkel är en vinkel större än 180 grader, betrakta den som en del av en cirkel. Graderna av reflexvinkeln och graderna av den mindre spetsiga vinkeln summerar till 360.
Tips
- Se till att din vetenskapliga kalkylators trigonometriska funktioner är inställda i grader, inte radianer.
- Lutningen är förhållandet mellan x-rörelsen och y-rörelsen. Måttenheten du använder för att kvantifiera längden på de två linjerna är irrelevant - se bara till att du använder samma enhet för båda linjerna. Med andra ord, om du mäter längden på en linje i centimeter måste du också mäta den andra i centimeter.
Förnödenheter
- Vetenskaplig kalkylator
- Linjal
"Mäta en vinkel utan gradskiva"
Оцените, пожалуйста статью
