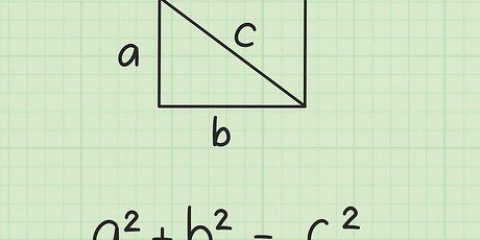
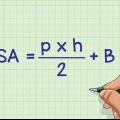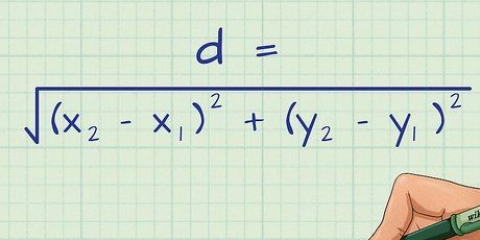Rätta vinklar anges ofta i läroböcker och prov med en liten fyrkant i det högra hörnet. Denna speciella märkning betyder "90 grader." 
Om din triangel har sidorna 3 och 4, och du har tilldelat bokstäver till dessa sidor så att a = 3 och b = 4, räknar du ut ekvationen som: 3 + 4 = c. 
Om a = 3, a = 3 x 3 eller 9.Om b = 4, då är b = 4 x 4 eller 16. När du räknar in dessa värden i din ekvation bör det nu se ut så här: 9 + 16 = c. 
I vårt exempel, 9 + 16 = 25, notera då 25 = c. 
I vårt exempel, c = 25.Kvadratroten ur 25 är 5 (5 x 5 = 25, Så Sqrt(25) = 5).Och det betyder c = 5, längden på vår hypotenusa! 

Du beräknar hypotenusan för denna triangel baserat på längden på ett av benen och multiplicerar dess längd med Sqrt(2). Det är bra att känna till detta förhållande, särskilt om dina test- eller läxproblem ger dig längderna på sidorna i form av variabler istället för heltal. 
Givet längden på det kortaste benet (det som är mitt emot 30 graders vinkeln), multiplicera längden på det benet med 2 för att få längden på hypotenusan. Till exempel om längden på det kortaste benet 4 är, då vet du att hypotenusan 8 måste vara. Om du vet längden på det längre benet (motsatt 60 graders vinkel), multiplicera den längden med2/Sqrt(3) för att hitta längden på hypotenusan.Till exempel om längden på det kortaste benet 4 är, då vet du att hypotenusan 4,62 måste vara. 

För att hitta sinus för en 80-graders vinkel kommer du att göra det synd 80 måste skriva följt av likhetstecknet eller Enter, eller80 synd. (Svaret är -0,9939.) Du kan också söka efter "sin kalkylator" med din webbläsare för några lättanvända miniräknare så att du inte behöver gissa. 
Sinusregeln kan faktiskt användas för att lösa för varje triangel, men bara en rätvinklig triangel kommer att ha en hypotenusa. 

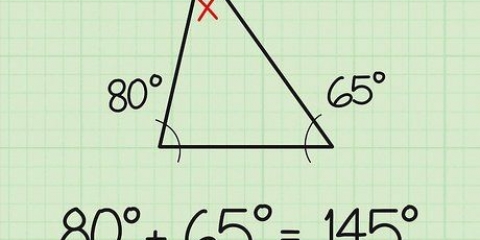
Till exempel om du vet det A = 40 grader, sedan B = 180 – (90 + 40). Förenkla detta till B = 180 – 130 och det kan du snabbt härleda B = 50 grader. 
För att fortsätta med vårt exempel, låt oss säga att längden på sidan a = 10.Vinkel C = 90 grader, vinkel A = 40 grader och vinkel B = 50 grader. 

Utgående från vårt exempel ser vi det synd 40 = 0,64278761.För att hitta värdet på c dividerar vi längden av a med detta tal och hittar det 10 / 0,64278761 = 15,6, längden på vår hypotenusa!
Bestämma längden på hypotenusan
Alla räta trianglar har en rät vinkel (90 grader), och hypotenusan är den sida som är motsatt den vinkeln. Hypotenusan är den längsta sidan av triangeln, och är också mycket lätt att hitta med ett antal olika metoder. Den här artikeln kommer att lära dig hur du bestämmer längden på hypotenusan med hjälp av Pythagoras sats, förutsatt att du vet längden på de andra två sidorna av triangeln. Då lär du dig att beräkna hypotenusan för några speciella räta trianglar som du ofta kommer att stöta på i tester. Och slutligen kommer du att lära dig hur man beräknar längden på hypotenusan med hjälp av sinusregeln, när endast längden på en av sidorna är känd och storleken på en av vinklarna är känd.
Steg
Metod 1 av 3: Använda Pythagoras sats

1. Lär dig Pythagoras sats. Pythagoras sats beskriver förhållandet mellan sidorna i en rätvinklig triangel. Den säger att för en godtycklig rätvinklig triangel med sidorna a och b, och hypotenusan med längden c, har vi a + b = c.

2. Se till att din triangel är en rätvinklig triangel.Pythagoras sats fungerar bara för räta trianglar, och per definition kan bara en rätvinklig triangel ha en hypotenusa.Om din triangel innehåller en vinkel på exakt 90 grader, är det en rätvinklig triangel och du kan fortsätta.

3. Tilldela variablerna a, b och c till sidorna av din triangel.Variabeln "c" är alltid tilldelad hypotenusan, d.v.s. den längsta sidan.Välj en av de andra sidorna för a, och namnge den återstående sidan b (det spelar ingen roll vilken, matematiken förblir densamma).Bearbeta sedan längderna av a och b till formeln, som visas i följande exempel:

4. Bestäm kvadraterna av a och b.För att hitta kvadraten på ett tal, multiplicera bara det talet med sig självt, så a = a x a. Hitta kvadraterna för både a och b och infoga dem i formeln.

5. Räkna värdena påa och b tillsammans på. Ta med detta i din ekvation och det ger dig värdet av c. Nu återstår bara ett steg och du har bestämt hypotenusan!

6. Bestäm kvadratroten ur c. Använd kvadratrotsfunktionen på din miniräknare (eller multiplikationstabeller, om du kan dem utantill) för att hitta kvadratroten ur c. Svaret är längden på din hypotenusa!
Metod 2 av 3: Bestämning av hypotenusan för speciella rätvinkliga trianglar

1. Lär dig känna igen trianglarna i en pythagoras trekant. Längden på sidorna av en pythagoras triad är heltal som följer Pythagoras sats. Du kommer regelbundet att stöta på dessa speciella trianglar i geometriläroböcker och i standardtest som SAT och GRE.I synnerhet, om du memorerar de första 2 Pythagoras trianglar, kan du spara mycket tid på dessa tester eftersom du omedelbart vet hypotenusan för någon av dessa trianglar bara genom att titta på längderna på sidorna!
- Den första Pythagoras trion är 3-4-5 (3 + 4 = 5, 9 + 16 = 25).När du ser en rätvinklig triangel med sidorna av längden 3 och 4 vet du genast säkert att hypotenusan blir 5 utan att behöva göra några beräkningar.
- Förhållandet mellan en Pythagoras trippel förblir densamma även när sidorna multipliceras med ett annat tal. Till exempel: en rätvinklig triangel med sidor 6 och 8 kommer att ha en hypotenusa på 10 (6 + 8 = 10, 36 + 64 = 100).Det samma gäller för9-12-15, även 1,5-2-2,5.Gör beräkningarna så får du se!
- Den andra pytagoreiska trion som du ofta kommer att stöta på i tester är 5-12-13 (5 + 12 = 13, 25 + 144 = 169).Se också upp för dess pluralformer, som t.ex 10-24-26 och 2,5-6-6,5.

2. Lär dig förhållandet mellan sidorna i en rätvinklig triangel med vinklarna 45-45-90. En 45-45-90 rätvinklig triangel har vinklar på 45, 45 och 90 grader, och kallas även för en likbent rätvinklig triangel. Den här finns ofta i standardtester och är en mycket enkel triangel att lösa. Förhållandet mellan sidorna i denna triangel är 1:1:Sqrt(2), vilket betyder att längden på benen är lika stor, och längden på hypotenusan är då helt enkelt längden på benen multiplicerad med kvadratroten ur två.

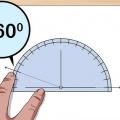
3. Lär dig proportionerna för en rät vinkel 30-60-90 triangel. Denna triangel har vinklar på 30, 60 och 90 grader och kan göras genom att dela en liksidig triangel på mitten. Sidorna i den räta triangeln 30-60-90 har alltid förhållandet 1:Sqrt(3):2, eller x:Sqrt(3)x:2x.Om man får längden på ett ben i den högra 30-60-90 triangeln och ombeds att bestämma hypotenusan, är det mycket lätt att göra:
Metod 3 av 3: Beräkna hypotenusan med sinusregeln

1. Förstå vad "Sinus" betyder att. Villkoren "sinus," "cosinus" och "tangent" alla hänvisar till vissa proportioner mellan vinklarna och/eller sidorna i en rätvinklig triangel.I en rätvinklig triangel, är sinus av en vinkel definierad som längden på sidan som är motsatt vinkeln delat med triangelns hypotenusa. Förkortningen för sinus som den visas på din miniräknare är synd.

2. Lär dig hur du beräknar sinus. Även en enkel vetenskaplig miniräknare har en sinusfunktion. Titta på nyckeln som är markerad synd.För att hitta sinus för en vinkel trycker du vanligtvis på synd-knapp och knappa sedan in vinkeln i grader.På vissa miniräknare måste du dock först ange vinkeln i grader och sedan trycka på synd-tryck på knappen. Du måste experimentera med din miniräknare eller titta i manualen för att avgöra vilken det är.

3. Lär dig sinusregeln.Sinusregeln är ett användbart verktyg för att lösa triangelproblem. Du kan huvudsakligen använda den för att hitta hypotenusan för en rätvinklig triangel, om du känner till längden på en sida och en annan av dess vinklar än den räta vinkeln. För alla triangel med sidor a, b och c och hörnen a, B och C, sinusregeln säger att en / synd a = b / synd B = c / synd C.

4. Tilldela variablerna a, b och c till sidorna av din triangel. Hypotenusan (den längsta sidan) ska alltid vara "c" är. För enkelhets skull, märk sidan med känd längd som "a" och andra "b". Tilldela sedan variablerna A, B och C till triangelns hörn. Den räta vinkeln mittemot hypotenusan blir då "C".Hörnet mitt emot "a" är vinkel "a" och vinkeln på motsatt sida "b" är "B".

5. Beräkna den tredje vinkeln. Eftersom det är en rät vinkel vet du det redan C = 90 grader och du vet också vilken vinkel a eller B är. Eftersom summan av alla vinklar i en triangel alltid måste vara lika med 180 grader, är det lätt att beräkna den tredje vinkeln med formeln: 180 – (90 + A) = B. Du kan också vända denna ekvation så att 180 – (90 + B) = A.

6. Undersök din triangel.Vid denna punkt vet du alla vinklarna på triangeln och längden på sidan a. Nu är det dags att bearbeta dessa värden till sinusregeln, för att beräkna längden på de andra två sidorna.

7. Tillämpa sinusregeln på din triangel.Vi behöver bara bearbeta våra tal och lösa följande ekvation för att hitta längden på hypotenusan c: längd på sidan a / synd A = längden på sidan c / synd C.Detta kan fortfarande se lite skrämmande ut, men 90 graders sinus är en konstant och alltid lika med 1!Vår ekvation kan därför förenklas till: en / synd A = c/1, eller enklare en / synd A = c.

8. Dela längden på sidena genom vinkelns sinus a för att hitta längden på hypotenusan!Du kan beräkna detta i två separata steg, genom att först: synd Beräkna och skriv A, dividera sedan med a. Eller testa allt på en gång i din miniräknare. Om du gör detta, glöm inte parentesen efter delningstecknet.Till exempel, knappa in 10 / (synd 40) eller 10 / (40 synd), beroende på din miniräknare.
"Bestämma längden på hypotenusan"
Оцените, пожалуйста статью