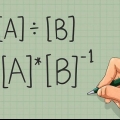Transponering av matris A = A Första kolumnen av A:
1
2
3 
a =
1 4 7
2 5 8
3 6 9 
matris z =
4 7 2 1
3 9 8 6 matris z =
4 3
7 9
2 8
1 6 
Om matris B är a m X n matris (m rader och n kolumner), då är den transponerade matrisen B a n X m matris (n rader och m kolumner). För varje element bxy (X-de, y-kolumnen) i B har matrisen B ett lika stort element på byx (y-raden, X-kolumnen). 

Om du inte kan visualisera detta, rita en 4x4-matris på ett papper. Vik nu över huvuddiagonalen. Ser du hur element a14 och a41 röra vid varandra? De byter plats i transponeringen, precis som alla andra par som rör vid varandra när de är vikta. 


Komplex konjugation av C =
2-i 3+2i
0-i 5-0i 
Konjugerad transponering av C = C =
2-i 0-i
3+2i 5-0i
Transponera en matris
En matristransposition är ett användbart matematiskt verktyg för att förstå matrisernas struktur. Funktioner som du kanske redan känner till från matriser, som att vara kvadratisk och symmetri, påverkar transponeringsresultaten på ett uppenbart sätt. Transposition tjänar också till att uttrycka vektorer som matriser, eller beräkna produkter av vektorer. När du hanterar komplexa matriser kommer det närbesläktade konceptet med en konjugerad transponering att hjälpa dig med många problem.
Steg
Del 1 av 3: Transponering av en matris

1. Börja med valfri matris. Du kan transponera vilken matris som helst oavsett antalet rader och kolumner. Kvadratiska matriser, med lika många rader och kolumner, transponeras mest, så vi använder en enkel kvadratisk matris som exempel:
- matris a =
1 2 3
4 5 6
7 8 9

2. Gör den första raden i matrisen till den första kolumnen i transponeringen. Skriv om rad ett i matrisen som en kolumn:
1
2
3

3. Upprepa för de återstående raderna. Den andra raden i den ursprungliga matrisen blir den andra kolumnen i transponeringen. Upprepa det här mönstret tills du har förvandlat varje rad till en kolumn:
1 4 7
2 5 8
3 6 9

4. Öva på en icke-fyrkantig matris. Transponeringen är exakt densamma för en icke-kvadratmatris. Du skriver om den första raden som den första kolumnen, den andra raden som den andra kolumnen och så vidare. Här är ett färgkodat exempel som visar var elementen hamnar:
4 7 2 1
3 9 8 6
4 3
7 9
2 8
1 6

5. Uttryck transponeringen matematiskt. Konceptet är ganska enkelt, men det är bra att kunna beskriva det i matematiska termer. Ingen jargong behövs utanför grundläggande matrisnotation:
Del 2 av 3: Specialfall

1. (M = M. Transponeringen av en transponering är den ursprungliga matrisen. Detta är mycket vettigt, eftersom du bara byter rader och kolumner. Om du byter dem igen kommer du tillbaka till början.

2. Luta kvadratiska matriser över huvuddiagonalen. I en kvadratisk matris kommer en transponering att "luta" matrisen längs huvuddiagonalen. Med andra ord, elementen i en diagonal linje av element a11 i det nedre högra hörnet förblir detsamma. De andra elementen kommer att röra sig över diagonalen och hamna på samma avstånd från diagonalen, på motsatt sida.

3. Transponera en symmetrisk matris. En symmetrisk matris är symmetrisk kring huvuddiagonalen. Om vi använder `tilt` eller `fold` enligt beskrivningen ovan kan vi direkt se att ingenting förändras. Alla elementpar som byter plats var redan identiska. Faktum är att detta är standardsättet att definiera en symmetrisk matris. Om matris A = A är matris A symmetrisk.
Del 3 av 3: Konjugerad transponering av en komplex matris

1. Börja med en komplex matris. Komplexa matriser har element med en verklig och imaginär komponent. Även om du kan ta en vanlig transponering av dessa matriser, är de flesta praktiska beräkningar konjugerade transpositioner istället.
- Matris C =
2+i 3-2i
0+i 5+0i

2. Ta den komplexa konjugationen. Den komplexa konjugationen ändrar tecknet för de imaginära komponenterna, utan att ändra de verkliga komponenterna. Utför denna operation för alla element i matrisen.
2-i 3+2i
0-i 5-0i

3. Transponera resultaten. Ta en vanlig konvertering av resultatet. Matrisen du slutar med är den konjugerade transponeringen av den ursprungliga matrisen.
2-i 0-i
3+2i 5-0i
Tips
- Den här artikeln använder notationen A för att beteckna omvandlingen av matris A. Beteckningen A` eller à betyder detsamma.
- Den här artikeln hänvisar till den konjugerade omvandlingen av matris A som A, den vanligaste notationen i linjär algebra. Kvantfysiker använder ofta A istället. A* är ett annat alternativ, men försök att undvika detta eftersom vissa källor kommer att använda denna symbol för att indikera en komplex konjugation.
"Transponera en matris"
Оцените, пожалуйста статью