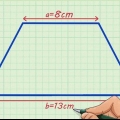
Om du till exempel har en trapets med en topp på 2 cm, en botten på 3 cm och två sidolängder på 1 cm, skulle din formel se ut så här:


Till exempel:


Trapetsens omkrets är därför 7 cm. 

Till exempel, om du har en trapets med en höjd av 6 cm, måste du rita en linje från varje övre vertex till botten. Notera 6 cm för varje rad. 
Till exempel, om toppen av trapetsen är 6 cm, är den mittersta delen av botten också 6 cm. 

Till exempel, om du vet att höjden på trapetsen är 6 cm och längden på sidan (hypotenus) är 9 cm, skulle din ekvation se ut så här:


Till exempel: är ekvationen  , sedan gör du kvadraten 6 och 9 och subtraherar kvadraten på 6 från kvadraten på 9:
, sedan gör du kvadraten 6 och 9 och subtraherar kvadraten på 6 från kvadraten på 9:




Till exempel:




Så notera som bas för den första triangeln.
som bas för den första triangeln. 
Till exempel, om den andra sidan av trapetsen är 7 cm, beräkna enligt följande:





Så notera som basen i den andra triangeln.
som basen i den andra triangeln. 
Till exempel: 
Efter att ha konverterat kvadratrötterna till decimaler har du
Så, den ungefärliga omkretsen av din trapets är 38,314 cm.. 

Till exempel, om du har en trapets med en höjd av 6 cm, dra en linje från varje topppunkt till botten. Notera 6 cm vid varje rad. 
Till exempel, om toppen av trapetsen är 6 cm, är den mittersta delen av botten också 6 cm. 
Med detta förhållande kan du hitta längden på triangelns hypotenusa, som också är den första sidan av trapetsen. Hypotenusan är sidan mitt emot 90 graders vinkeln i en rätvinklig triangel. 
Anta att den givna inre vinkeln är 35 grader och triangelns höjd är 6 cm, då kommer din formel att se ut så här:


Om du till exempel använder en miniräknare kommer du att upptäcka att sinus för en 35 graders vinkel är 0,5738 (avrundat). Så din formel är nu:


Till exempel:




Således är längden på hypotenusan och den första saknade sidan av trapetsen cirka 10,4566 cm. 
Till exempel, om den givna inre vinkeln är 45 grader, beräkna:





Så längden på hypotenusan och den andra saknade sidan av trapetsen är cirka 8,4854 cm. 

Till exempel, om den första räta triangeln har en hypotenusa på 10,4566 och en höjd på 6, är din formel:


Till exempel:






Så basen av triangeln och den första saknade delen av botten av trapetsen är cirka 8,5639 cm. 
Till exempel, om den andra räta triangeln har en hypotenusa på 8,4854 och en höjd på 6, skulle du beräkna enligt följande:






Så basen av den andra triangeln, och den andra saknade delen av trapetsens botten, är lika med 6 cm. 
Till exempel: 
Så den ungefärliga omkretsen av trapetsen är 45,5059 cm.
Beräkna omkretsen av en trapets
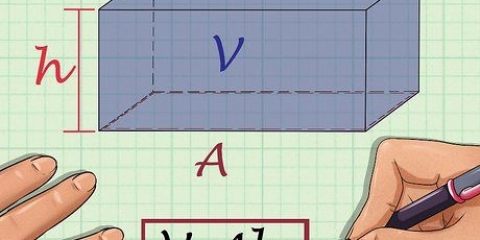
En trapets definieras som en fyrhörning med två parallella sidor. Som med alla polygoner måste du lägga till alla fyra sidorna för att hitta omkretsen av en trapets (eller trapets). Ofta kommer du dock att missa sidolängder, men du har andra data, som höjden på trapetsen eller vinkelmåtten. Med hjälp av dessa data kan du hitta de okända längderna på sidorna med hjälp av reglerna för geometri och trigonometri.
Steg
Metod 1 av 3: Om du vet längden på båda sidorna och basen

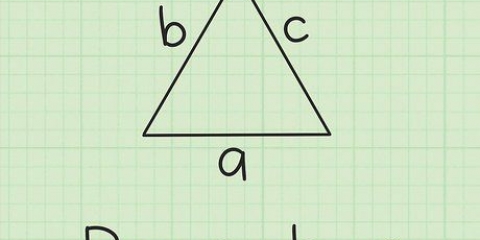
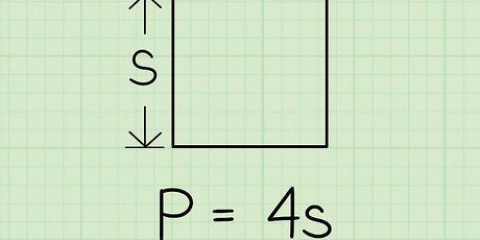
1. Ställ in formeln för omkretsen av en trapets. Formeln är  , varigenom
, varigenom  är lika med trapetsens omkrets och variabeln
är lika med trapetsens omkrets och variabeln  är lika med längden på toppen av trapetsen,
är lika med längden på toppen av trapetsen,  är lika med bottens längd,
är lika med bottens längd,  är lika med längden på vänster sida och
är lika med längden på vänster sida och  är lika med längden på höger sida.
är lika med längden på höger sida.
 , varigenom
, varigenom  är lika med trapetsens omkrets och variabeln
är lika med trapetsens omkrets och variabeln  är lika med längden på toppen av trapetsen,
är lika med längden på toppen av trapetsen,  är lika med bottens längd,
är lika med bottens längd,  är lika med längden på vänster sida och
är lika med längden på vänster sida och  är lika med längden på höger sida.
är lika med längden på höger sida.
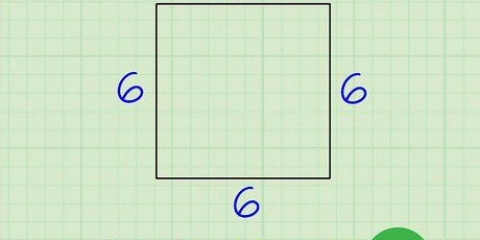
2. Använd sidlängderna i formeln. Om du inte vet längden på alla fyra sidorna av trapetsen kan du inte använda den här formeln.


3. Lägg ihop sidolängderna. Detta kommer att ge dig omkretsen av din trapets.


Trapetsens omkrets är därför 7 cm.
Metod 2 av 3: Om du känner till höjden, båda sidlängderna och topplängden

1. Dela trapetsen i en rektangel och två räta trianglar. För att göra detta, rita höjden från båda övre hörnen.
- Om du inte kan bilda de två räta trianglarna eftersom en sida av trapetsen är vinkelrät mot basen, se till att denna sida är lika lång som höjden och dela trapetsen i en rektangel och en rätvinklig triangel.

2. Ange längden på varje konturlinje. Eftersom dessa är de motsatta sidorna av en rektangel kommer de att vara lika långa.

3. Notera längden på den mittersta delen av botten. (Detta är botten av rektangeln.) Längden kommer att vara lika med längden på toppen (överdelen av rektangeln), eftersom de motsatta sidorna av en rektangel är lika långa. Om du inte vet längden på toppen kan du inte använda den här metoden.

4. Ställ upp Pythagoras sats för den första räta triangeln. Formeln är  , varigenom
, varigenom  är längden på hypotenusan i den räta triangeln (sidan mitt emot den räta vinkeln),
är längden på hypotenusan i den räta triangeln (sidan mitt emot den räta vinkeln),  är höjden på den räta triangeln och
är höjden på den räta triangeln och  är längden på triangelns bas.
är längden på triangelns bas.
 , varigenom
, varigenom  är längden på hypotenusan i den räta triangeln (sidan mitt emot den räta vinkeln),
är längden på hypotenusan i den räta triangeln (sidan mitt emot den räta vinkeln),  är höjden på den räta triangeln och
är höjden på den räta triangeln och  är längden på triangelns bas.
är längden på triangelns bas.
5. Använd de kända värdena för den första triangeln i formeln. Se till att ange sidolängden på trapetsen för  . Ange höjden på trapetsen för
. Ange höjden på trapetsen för  .
.
 . Ange höjden på trapetsen för
. Ange höjden på trapetsen för  .
.

6. Kvadra de kända värdena i ekvationen. Subtrahera sedan de kvadratiska värdena från varandra för att få  att isolera.
att isolera.
 att isolera.
att isolera. , sedan gör du kvadraten 6 och 9 och subtraherar kvadraten på 6 från kvadraten på 9:
, sedan gör du kvadraten 6 och 9 och subtraherar kvadraten på 6 från kvadraten på 9:



7. Ta kvadratroten för att få värdet av b  att hitta. (För fullständiga instruktioner om att förenkla kvadratrötter, läs denna artikel om ämnet). Resultatet kommer att ge dig värdet av den saknade basen i din första räta triangel. Skriv denna längd vid basen av din triangel.
att hitta. (För fullständiga instruktioner om att förenkla kvadratrötter, läs denna artikel om ämnet). Resultatet kommer att ge dig värdet av den saknade basen i din första räta triangel. Skriv denna längd vid basen av din triangel.
 att hitta. (För fullständiga instruktioner om att förenkla kvadratrötter, läs denna artikel om ämnet). Resultatet kommer att ge dig värdet av den saknade basen i din första räta triangel. Skriv denna längd vid basen av din triangel.
att hitta. (För fullständiga instruktioner om att förenkla kvadratrötter, läs denna artikel om ämnet). Resultatet kommer att ge dig värdet av den saknade basen i din första räta triangel. Skriv denna längd vid basen av din triangel.



Så notera
 som bas för den första triangeln.
som bas för den första triangeln.
8. Hitta den saknade längden på den andra räta triangeln. För att göra detta, ställ in Pythagoras sats för den andra triangeln och följ stegen för att hitta längden på den saknade sidan. Om du arbetar med en likbent trapets (den där de två icke-parallella sidorna har samma längd), så är de två räta trianglarna kongruenta, så värdet på den första triangeln är lika med värdet för den andra triangeln.





Så notera
 som basen i den andra triangeln.
som basen i den andra triangeln.
9. Lägg ihop alla sidolängder på trapetsen. Omkretsen av en polygon är summan av alla sidor:  . För botten, lägg till undersidan av rektangeln, plus baserna för de två trianglarna. Du kommer förmodligen att ha kvadratrötter i ditt svar. För fullständiga instruktioner om hur du lägger till kvadratrötter, läs artikeln om detta ämne. Du kan också använda en kalkylator för att konvertera kvadratrötterna till decimaler.
. För botten, lägg till undersidan av rektangeln, plus baserna för de två trianglarna. Du kommer förmodligen att ha kvadratrötter i ditt svar. För fullständiga instruktioner om hur du lägger till kvadratrötter, läs artikeln om detta ämne. Du kan också använda en kalkylator för att konvertera kvadratrötterna till decimaler.
 . För botten, lägg till undersidan av rektangeln, plus baserna för de två trianglarna. Du kommer förmodligen att ha kvadratrötter i ditt svar. För fullständiga instruktioner om hur du lägger till kvadratrötter, läs artikeln om detta ämne. Du kan också använda en kalkylator för att konvertera kvadratrötterna till decimaler.
. För botten, lägg till undersidan av rektangeln, plus baserna för de två trianglarna. Du kommer förmodligen att ha kvadratrötter i ditt svar. För fullständiga instruktioner om hur du lägger till kvadratrötter, läs artikeln om detta ämne. Du kan också använda en kalkylator för att konvertera kvadratrötterna till decimaler.
Efter att ha konverterat kvadratrötterna till decimaler har du

Så, den ungefärliga omkretsen av din trapets är 38,314 cm..
Metod 3 av 3: Om du känner till höjden, längden på de övre och nedre inre hörnen

1. Dela trapetsen i en rektangel och två räta trianglar. För detta, ange höjden från båda övre hörnen.
- Om du inte kan bilda två räta trianglar eftersom en sida av trapetsen är vinkelrät mot basen, se till att denna sida är lika stor som höjden och dela trapetsen i en rektangel och en rätvinklig triangel.

2. Märk varje kontur. Eftersom dessa är motsatta sidor av en rektangel kommer de att ha samma längd.

3. Notera längden på den mittersta delen av botten. (Detta är botten av rektangeln.) Denna längd kommer att vara lika med längden på toppen, eftersom de motsatta sidorna av en rektangel är lika långa.

4. Ställ in sinusformeln för den första räta triangeln. Formeln är  , varigenom
, varigenom  det inre hörnet är,
det inre hörnet är,  triangelns höjd och
triangelns höjd och  är hypotenusans längd.
är hypotenusans längd.
 , varigenom
, varigenom  det inre hörnet är,
det inre hörnet är,  triangelns höjd och
triangelns höjd och  är hypotenusans längd.
är hypotenusans längd.
5. Använd de kända värdena i sinusförhållandet. Se till att använda triangelns höjd som längden på den motsatta sidan i formeln. du löser detta för H.


6. Bestäm sinus för vinkeln. Gör detta med hjälp av SIN-knappen på en vetenskaplig miniräknare. Använd detta värde i formeln.


7. Lös detta för H. För att göra detta, multiplicera varje sida med H och dividera sedan varje sida med sinusvinkeln. Eller dela triangelns höjd med sinusvinkeln.




Således är längden på hypotenusan och den första saknade sidan av trapetsen cirka 10,4566 cm.

8. Hitta längden på hypotenusan i den andra räta triangeln. Ställ in sinusformeln ( ) för den andra givna inre vinkeln. Detta kommer att ge dig längden på hypotenusan, som också är den första sidan av trapetsen.
) för den andra givna inre vinkeln. Detta kommer att ge dig längden på hypotenusan, som också är den första sidan av trapetsen.
 ) för den andra givna inre vinkeln. Detta kommer att ge dig längden på hypotenusan, som också är den första sidan av trapetsen.
) för den andra givna inre vinkeln. Detta kommer att ge dig längden på hypotenusan, som också är den första sidan av trapetsen.




Så längden på hypotenusan och den andra saknade sidan av trapetsen är cirka 8,4854 cm.

9. Ställ upp Pythagoras sats för den första räta triangeln. Pythagoras sats är högljudd  , där hypotenusans längd är lika med
, där hypotenusans längd är lika med  , och triangelns höjd
, och triangelns höjd  .
.
 , där hypotenusans längd är lika med
, där hypotenusans längd är lika med  , och triangelns höjd
, och triangelns höjd  .
.
10. Använd de kända värdena i Pythagoras sats för den första räta triangeln. Se till att du anger rätt värde för hypotenusan  och höjden
och höjden  .
.
 och höjden
och höjden  .
.

11. Lös detta för b  . Detta ger dig längden på basen av den första räta triangeln, och den första saknade delen av basen av trapetsen.
. Detta ger dig längden på basen av den första räta triangeln, och den första saknade delen av basen av trapetsen.
 . Detta ger dig längden på basen av den första räta triangeln, och den första saknade delen av basen av trapetsen.
. Detta ger dig längden på basen av den första räta triangeln, och den första saknade delen av basen av trapetsen.





Så basen av triangeln och den första saknade delen av botten av trapetsen är cirka 8,5639 cm.

12. Hitta längden på den saknade basen i den andra räta triangeln. Använd Pythagoras sats ( ). Använd hypotenusans längd för
). Använd hypotenusans längd för  och höjden för
och höjden för  . Lös detta för
. Lös detta för  och du får längden på den andra saknade delen av botten trapetsen.
och du får längden på den andra saknade delen av botten trapetsen.
 ). Använd hypotenusans längd för
). Använd hypotenusans längd för  och höjden för
och höjden för  . Lös detta för
. Lös detta för  och du får längden på den andra saknade delen av botten trapetsen.
och du får längden på den andra saknade delen av botten trapetsen.





Så basen av den andra triangeln, och den andra saknade delen av trapetsens botten, är lika med 6 cm.

13. Lägg ihop alla sidor av trapetsen. Omkretsen av en polygon är summan av alla sidor:  . För botten, lägg till botten av rektangeln till basen av de två trianglarna.
. För botten, lägg till botten av rektangeln till basen av de två trianglarna.
 . För botten, lägg till botten av rektangeln till basen av de två trianglarna.
. För botten, lägg till botten av rektangeln till basen av de två trianglarna.
Så den ungefärliga omkretsen av trapetsen är 45,5059 cm.
Tips
- Använd specialtrianglarnas lagar för att hitta de saknade längderna av specialtrianglar, utan att använda sinusformeln eller Pythagoras sats. Lagarna gäller för en 30-60-90 triangel, eller en 90-45-45 triangel.
- Använd en vetenskaplig kalkylator för att bestämma sinus för en vinkel, genom att ange vinkeln och sedan trycka på `SIN`-knappen. Du kan också använda en trigonometritabell.
Förnödenheter
- Kalkylator
- Penna
- Papper
"Beräkna omkretsen av en trapets"
Оцените, пожалуйста статью