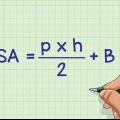Att bestämma determinanten för en 3x3-matris: 12 steg (med bilder)

Steg
- Del 1 av 2: Fastställande av determinant
- Del 2 av 2: Förenkla problemet
Tips

Determinanten för en matris används flitigt inom matematik, linjär algebra och högre geometri. Utanför den vetenskapliga världen använder datorgrafikingenjörer och programmerare ofta matrisernas bestämningsfaktorer. Läs den här artikeln för att bestämma determinanten för en 3x3-matris.

Steg

Del 1 av 2: Fastställande av determinant

1. Skriv ner din 3 x 3 matris. Vi börjar med en 3 x 3 matris A och provar determinanten |A| att gilla det. Vi använder följande allmänna notation för matrisen (och detta är vår exempelmatris):

$m = (\begin{matrix} a \end{matrix} 11 a_{12} a_{13} a_{21} & a_{22} & a_{23} a_{31} & a_{32} & a_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & 7 \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4&7\4&6&2end{pmatrix}}$

Bild med titeln Hitta determinanten för en 3X3-matris Steg 2

2. Välj en rad eller kolumn. Detta kommer att vara din referensrad eller kolumn. Du får samma svar oavsett vilken du väljer. Välj nu bara den första raden. Senare kommer vi att ge dig råd om hur du väljer det alternativ som är lättast att beräkna.

Låt oss välja den första raden i vår exempelmatris A. Ringa in 1 5 3. Generellt sett ringa in a₁₁ a₁₂ a₁₃.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 3

3. Kryssa över raden och kolumnen för det första elementet. Titta på raden eller kolumnen du ringde in och välj det första elementet. Rita en linje genom motsvarande rad och kolumn. Om allt går bra ger detta nu fyra siffror. Vi behandlar detta som en 2 x 2 matris.

I vårt exempel är referensraden 1 5 3. Det första elementet finns på rad 1 och kolumn 1. Stryk rad 1 och kolumn 1 helt. Skriv ner de återstående elementen som ett2 x 2 matris:

~~1 5 3~~
2 4 7
4 6 2

Bild med titeln Hitta determinanten för en 3X3-matris Steg 4

4. Bestäm determinanten för 2 x 2-matrisen. Glöm inte: matrisen

(\begin{matrix} a & b \\ c & d \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ har en bestämningsfaktor för ad - f.Kr. Det vet du genom att dra ett kryss (X) genom 2 x 2-matrisen. Multiplicera de två talen som är förbundna med i X. Subtrahera sedan produkten av de två talen som är förbundna med /. Använd den här formeln för att beräkna determinanten för matrisen du just hittade.

I vårt exempel är matrisens determinant

(\begin{matrix} 4 & 7 \\ 6 & 2 \end{matrix})

${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Denna determinant kallas mindre av elementet vi valde i vår ursprungliga matris. I det här fallet har vi den minderårige av a₁₁ hittade det.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 5

5. Multiplicera svaret med ditt valda element. Kom ihåg att du valde ett element från din referensrad (eller kolumn) när du bestämde vilken rad och kolumn som skulle strykas över. Multiplicera detta element med den determinant du just beräknade för 2x2-matrisen.

I vårt exempel har vi en₁₁ vald, som har värdet 1. Multiplicera detta med -34 (determinanten för 2x2-matrisen) för att få 1*-34 = -34 att få.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 6

6. Bestäm tecknet på ditt svar. Multiplicera nu svaret med 1 eller med -1 för att få kofaktor av ditt valda element. Vilken du använder beror på elementets position i 3x3-matrisen. Memorera följande enkla tabell för att ta reda på vilket element som orsakar vad:

+ - +
- + -
+ - +

För att vi a₁₁ har valt, markerat med ett +, multiplicerar vi talet med +1 (med andra ord, vi gör ingenting med det). Svaret är fortfarande -34.

Ett annat sätt att bestämma tecknet är med formeln (-1), där i och j bildar elementets rad och kolumn.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 7

7. Upprepa denna process för det andra elementet i din referensrad eller kolumn. Fortsätt med den ursprungliga 3x3-matrisen, med raden eller kolumnen du cirklade in tidigare. Upprepa samma process med detta element:

Korsa raden och kolumnen för det elementet. I det här fallet väljer du elementet a₁₂ (med värde 5). Korsa den första raden (1 5 3) och den andra kolumnen

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Behandla de återstående elementen som en 2x2-matris. I vårt exempel är matrisen

(\begin{matrix} 2 & 7 \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Bestäm determinanten för denna 2x2-matris. Använd formeln ad - bc. (2*2 - 7*4 = -24)

Multiplicera detta med det valda elementet i 3x3-matrisen. -24 * 5 = -120

Bestäm om du ska multiplicera med -1. Använd teckentabellen eller formeln (-1). Vi har element a₁₂ valt, och det är en – på teckentabellen. Vi måste ändra tecknet på vårt svar: (-1)*(-120) = 120.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 8

8. Upprepa för det tredje elementet. Du måste nu hitta en kofaktor. Beräkna i för den tredje termen i din referensrad eller kolumn. Här är en snabb förklaring av hur man beräknar kofaktorn för ₁₃ i vårt exempel:

Korsa rad 1 och kolumn 3 och få

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2&4\4&6end{pmatrix}}$

Dess determinant är 2*6 - 4*4 = -4.

Multiplicera detta med elementet a₁₃: -4 * 3 = -12.

element a₁₃ är ett + på teckentabellen, så svaret är -12.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 9

9. Lägg ihop de tre resultaten. Detta är det sista steget. Du beräknade kofaktorer, en för varje element i en enda rad eller kolumn. Lägg ihop dessa och du har hittat determinanten för 3x3-matrisen.

I vårt exempel är determinanten -34 + 120 + -12 = 74.

Del 2 av 2: Förenkla problemet

Bild med titeln Hitta determinanten för en 3X3-matris Steg 10

1. Välj referensen med flest nollor. Glöm inte att du varje kan välja rad eller kolumn som referens. Du får samma svar oavsett vad du väljer. Om du väljer en rad eller kolumn med nollor behöver du bara beräkna kofaktorn för de element som inte är noll. Anledningen är följande:

Anta att du väljer rad 2, med elementen a₂₁, a₂₂, och a₂₃. För att lösa detta problem tittar vi på tre olika 2x2-matriser. Anta att vi kallar detta A₂₁, a₂₂ och A₂₃.
Determinanten för 3x3-matrisen är a₂₁|A₂₁| - a₂₂|A₂₂| + a₂₃|A₂₃|.
Om villkoren a₂₂ och a₂₃ är båda 0, då blir vår formel₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| - 0 + 0 = a₂₁|A₂₁|. Nu behöver vi bara beräkna kofaktorn för ett enda element.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 11

2. Lägg ihop raderna för att förenkla matrisen. Om du tar värdena på en rad och lägger till dem i en annan rad kommer matrisens determinant inte att ändras. Detsamma gäller kolumner. Du kan göra detta upprepade gånger - eller multiplicera värdena med en konstant innan du lägger till - för att få så många nollor i matrisen som möjligt. Detta kan spara mycket arbete.

Anta till exempel att du har en 3x3-matris:

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

Var 9:e i position a₁₁ för att bli av med det kan vi multiplicera den andra raden med -3 och lägga till resultatet till den första. Den nya första raden blir då [9 -1 2] + [-9 -3 0] = [0 -4 2].

Den nya matrisen är

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Försök att använda samma knep för kolumnerna, att₁₂ att göra en 0.

Bild med titeln Hitta determinanten för en 3X3-matris Steg 12

3. Lär dig tricket för att lösa triangelmatriser. I dessa speciella fall är determinanten helt enkelt produkten av elementen längs huvuddiagonalen, från a₁₁ överst till vänster till a₃₃ nere till höger. Vi pratar fortfarande om 3x3 matriser, men "triangulära" matriser har speciella värdemönster som inte noll är:

Övre triangelmatris: Alla element som inte är noll är på eller över huvuddiagonalen. Alla värden nedan är noll.

Nedre triangelmatris: Alla element som inte är noll är på eller under huvuddiagonalen.

Diagonalmatris: Alla element som inte är noll är på huvuddiagonalen. (En delmängd av ovanstående.)

Tips

Denna metod kan användas för kvadratiska matriser av alla storlekar. Till exempel, om du använder detta för en 4x4-matris, så håller du efter "stryka" en 3x3-matris, för vilken du kan beräkna determinanten enligt ovan. Var varnad, för att göra detta för hand kommer att bli väldigt tråkigt!
Om alla element i en rad eller kolumn är lika med 0, är determinanten för den matrisen lika med 0.