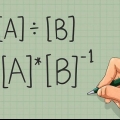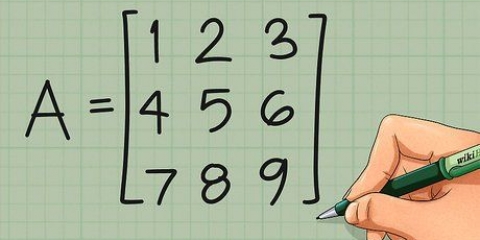Om du har fler variabler, fortsätt bara raden så länge det tar. Om du till exempel försökte lösa ett system med sex variabler, skulle din standardform se ut som Au+Bv+Cw+Dx+Ey+Fz=G. I den här artikeln kommer vi att fokusera på system med endast tre variabler. Att lösa ett större system är exakt samma sak, men tar bara mer tid och fler steg. Observera att i standardform är operationerna mellan termerna alltid ett tillägg. Om det finns en subtraktion i din ekvation, istället för en addition, måste du arbeta med detta senare genom att göra din koefficient negativ. För att göra detta lättare att komma ihåg kan du skriva om ekvationen och lägga till operationen och göra koefficienten negativ. Till exempel kan du skriva om ekvationen 3x-2y+4z=1 som 3x+(-2y)+4z=1. 
Anta att du har ett system som består av de tre ekvationerna 3x+y-z=9, 2x-2y+z=-3 och x+y+z=7. Den översta raden i din matris kommer att innehålla siffrorna 3, 1, -1, 9, eftersom dessa är koefficienterna och lösningen av den första ekvationen. Observera att varje variabel som inte har en koefficient antas ha en koefficient på 1. Den andra raden i matrisen blir 2, -2, 1, -3 och den tredje raden 1, 1, 1, 7. Se till att passa in x-koefficienterna i den första kolumnen, y-koefficienterna i den andra, z-koefficienterna i den tredje och lösningstermerna i den fjärde. När du är klar med att arbeta med matrisen kommer dessa kolumner att vara viktiga när du skriver din lösning. 

Du kan ange vilken specifik position som helst i en matris med en kombination av R och C. Till exempel, för att beteckna en term i den andra raden, tredje kolumnen, kan du kalla den R2C3. 

Det är vanligt att använda bråk i skalär multiplikation eftersom man ofta vill få en diagonal rad med 1:or. Vänj dig vid att arbeta med bråk. Det blir också lättare (för de flesta stegen i att lösa matrisen) att kunna skriva dina bråk i felaktig form och sedan konvertera dem tillbaka till blandade tal för den slutliga lösningen. Det är därför siffran 1 2/3 är lättare att arbeta med om du skriver den som 5/3. Till exempel börjar den första raden (R1) i vårt exempelproblem med termerna [3.1,-1,9]. Lösningsmatrisen måste innehålla en 1 i den första positionen på den första raden. För att "förvandla" 3:an till en 1:a kan vi multiplicera hela raden med 1/3. Detta skapar den nya R1 av [1.1/3,-1/3.3]. Se till att lämna eventuella negativa tecken där de hör hemma. 
Du kan använda förkortad notation och deklarera denna operation som R2-R1=[0,-1,2,6]. Kom ihåg att addition och subtraktion är precis motsatta former av samma operation. Du kan tänka på det som att lägga till två tal eller subtrahera motsatsen. Till exempel, om du börjar med den enkla ekvationen 3-3=0, kan du tänka på detta som ett additionsproblem av 3+(-3)=0. Resultatet är detsamma. Detta verkar enkelt, men det är ibland lättare att överväga ett problem i en eller annan form. Håll bara ett öga på dina negativa tecken. 
Par; att det finns en rad 1 av [1,1,2,6] och en rad 2 av [2,3,1,1]. Du vill ha en 0-term i den första kolumnen i R2. Det vill säga att du vill ändra 2:an till en 0. För att göra detta måste du subtrahera en 2:a. Du kan få en 2:a genom att först multiplicera rad 1 med skalär multiplikation 2, och sedan subtrahera den första raden från den andra raden. I förkortad form kan detta skrivas som R2-2*R1. Multiplicera först R1 med 2 för att få [2,2,4,12]. Subtrahera sedan detta från R2 för att få [(2-2),(3-2),(1-4),(1-12)]. Förenkla detta och din nya R2 blir [0,1,-3,-11]. 
Ett vanligt fel uppstår när man utför ett kombinerat multiplikations- och additionssteg i ett drag. Anta till exempel att du måste subtrahera R1 från R2 två gånger. När du multiplicerar R1 med 2 för att göra detta steg, kom ihåg att R1 inte ändras i matrisen. Du gör bara multiplikationen för att ändra R2. Kopiera R1 i sin ursprungliga form först och gör sedan ändringen till R2. 
1. Gör en 1 i första raden, första kolumnen (R1C1). 2. Gör en nolla i den andra raden, första kolumnen (R2C1). 3. Gör en 1 i andra raden, andra kolumnen (R2C2). 4. Gör en nolla i den tredje raden, första kolumnen (R3C1). 5. Gör en nolla i tredje raden, andra kolumnen (R3C2). 6. Gör en 1 i tredje raden, tredje kolumnen (R3C3). 
Skapa en nolla i den andra raden, tredje kolumnen (R2C3). Skapa en nolla i första raden, tredje kolumnen (R1C3). Skapa en 0 i första raden, andra kolumnen (R1C2). 


Observera att multiplikation och division bara är inversa funktioner av varandra. Vi kan säga att vi multiplicerar med 1/3 eller dividerar med 3, utan att ändra resultatet. 
Skriv rad 3 (som inte har ändrats) om R3=[1,1,1,7]. Var försiktig när du subtraherar negativa tal för att se till att tecknen förblir korrekta. Låt oss nu först sätta bråken i deras felaktiga form. Detta gör senare steg i lösningen enklare. Du kan förenkla bråken i det sista steget av problemet. 
Observera att om den vänstra halvan av sekvensen börjar se ut som lösningen med 0 och 1, kan den högra halvan se ful ut, med oegentliga bråk. Lämna dem bara för vad de är nu. Kom ihåg att fortsätta kopiera de opåverkade raderna, så R1=[1,1/3,-1/3,3] och R3=[1,1,1,7]. 
Fortsätt kopiera längs R1=[1.1/3,-1/3.3] och R2=[0.1,-5/8.27/8]. Kom ihåg att du bara byter en rad åt gången. 

Observera att de fraktioner som verkade ganska komplicerade i föregående steg redan börjar lösas. Fortsätt med R1=[1.1/3,-1/3.3] och R2=[0.1,-5/8.27/8]. Observera att du vid denna tidpunkt har diagonalen på 1:or för din lösningsmatris. Du behöver bara konvertera tre element i matrisen till nollor för att hitta din lösning. 
Ta sedan R1=[1,1/3,-1/3,3] och R3=[0,0,1,1]. 
Ta de oförändrade R2=[0,1,0,4] och R3=[0,0,1,1]. 

1002 0104 0011 


Eftersom varje ekvation förenklas till ett sant matematiskt påstående, är dina lösningar korrekta. Om någon av lösningarna inte är korrekt, kontrollera ditt arbete igen och leta efter eventuella fel. Några vanliga misstag uppstår när man blir av med minustecken på vägen eller när man förväxlar multiplikation och addition av bråk. 
Lös matriser
En matris är ett mycket användbart sätt att representera tal i ett blockformat, som du sedan kan använda för att lösa ett system av linjära ekvationer. Om du bara har två variabler kommer du förmodligen att använda en annan metod. Läs om detta i Lösa ett ekvationssystem för exempel på dessa andra metoder. Men om du har tre eller fler variabler är en matris idealisk. Genom att använda upprepade kombinationer av multiplikation och addition kan man systematiskt komma fram till en lösning.
Steg
Del 1 av 4: Rita upp matrisen

1. Kontrollera att du har tillräckligt med data. För att få en unik lösning för varje variabel i ett linjärt system med hjälp av en matris måste du ha lika många ekvationer som antalet variabler du försöker lösa. Till exempel: med variablerna x, y och z behöver du tre ekvationer. Om du har fyra variabler behöver du fyra ekvationer.
- Om du har färre ekvationer än antalet variabler kommer du att lära dig några gränser för variablerna (som x = 3y och y = 2z), men du kommer inte att kunna få en exakt lösning. För den här artikeln kommer vi bara att arbeta mot en unik lösning.

2. Skriv dina ekvationer i standardform. Innan du kan hälla data från ekvationerna till en matrisform skriver du först varje ekvation i standardform. Standardformen för en linjär ekvation är Ax+By+Cz=D, där de stora bokstäverna är koefficienterna (siffror), och den sista siffran (i det här exemplet, D) är till höger om likhetstecknet.

3. Placera talen från ekvationssystemet i en matris. En matris är en grupp av tal, ordnade i en sorts tabell, med vilken vi ska arbeta för att lösa systemet. Den innehåller i princip samma data som själva ekvationerna, men i ett enklare format. För att göra matrisen för dina ekvationer i standardform, kopiera helt enkelt koefficienterna och resultatet av varje ekvation till en enda rad och stapla dessa rader ovanpå varandra.

4. Rita en stor hakparentes runt hela matrisen. Enligt konventionen betecknas en matris med ett par hakparenteser, [ ], runt hela sifferblocket. Parenteserna påverkar inte lösningen på något sätt, men de indikerar att du arbetar med matriser. En matris kan bestå av valfritt antal rader och kolumner. I den här artikeln kommer vi att använda parenteser runt en rad termer för att indikera att de hör ihop.

5. Användning av vanlig symbolik. När man arbetar med matriser är det vanligt att man refererar till raderna med förkortningen R och kolumnerna med förkortningen C. Du kan använda siffror tillsammans med dessa bokstäver för att beteckna en specifik rad eller kolumn. Till exempel, för att indikera rad 1 i en matris, kan du skriva R1. Rad 2 blir då R2.
Del 2 av 4: Lära sig operationerna för att lösa ett system med en matris

1. Förstå formen på lösningsmatrisen. Innan du börjar lösa ditt ekvationssystem måste du förstå vad du ska göra med matrisen. Vid det här laget har du en matris som ser ut så här:
- 31-19
- 2-21-3
- 1117
- Du arbetar med ett antal grundläggande operationer för att skapa `lösningsmatrisen`. Lösningsmatrisen kommer att se ut så här:
- 100x
- 010y
- 001z
- Observera att matrisen består av 1:or på en diagonal linje med 0:or i alla andra utrymmen utom den fjärde kolumnen. Siffrorna i den fjärde kolumnen är lösningarna för variablerna x, y och z.

2. Använd skalär multiplikation. Det första verktyget till ditt förfogande för att lösa ett system med hjälp av en matris är skalär multiplikation. Detta är helt enkelt en term som betyder att du multiplicerar elementen i en rad i matrisen med ett konstant tal (inte en variabel). När du använder skalär multiplikation, kom ihåg att du måste multiplicera varje term i hela sekvensen med vilket tal du än väljer. Om du glömmer den första termen och bara multiplicerar så får du en felaktig lösning. Du behöver dock inte multiplicera hela matrisen samtidigt. Med skalär multiplikation arbetar du bara på en rad i taget.

3. Använd radaddition eller radsubtraktion. Det andra verktyget du kan använda är att lägga till eller subtrahera två rader av matrisen. För att skapa 0-termerna i din lösningsmatris måste du lägga till eller subtrahera tal för att komma till 0. Till exempel, om R1 i en matris är [1,4,3,2] och R2 är [1,3,5,8], så kan du subtrahera den första raden från den andra raden och skapa en ny rad [ 0,-1, 2,6], eftersom 1-1=0 (första kolumnen), 3-4=-1 (andra kolumnen), 5-3=2 (tredje kolumnen) och 8-2=6 (fjärde kolumnen) kolumn). När du utför en rad addition eller subtraktion, skriv om ditt nya resultat istället för raden du började med. I det här fallet skulle vi ta ut rad 2 och infoga den nya raden [0,-1,2,6].

4. Kombinera radaddition och skalär multiplikation i ett enda steg. Du kan inte förvänta dig att termerna alltid matchar, så kan använda en enkel addition eller subtraktion för att skapa nollor i din matris. Oftare måste du lägga till (eller subtrahera) en multipel av en annan rad. För att göra detta, gör den skalära multiplikationen först och lägg sedan till resultatet till målraden du försöker ändra.

5. Kopiera rader som förblir oförändrade medan du arbetar. När du arbetar med matrisen kommer du att ändra en enda rad åt gången, antingen genom skalär multiplikation, radaddition eller radsubtraktion, eller genom en kombination av steg. När du ändrar en rad, se till att kopiera de andra raderna i din matris i deras ursprungliga form.

6. Arbeta först uppifrån och ned. För att lösa systemet arbetar du i ett mycket organiserat mönster, och "löser" i princip en term i matrisen åt gången. Ordningen för en array med tre variabler kommer att se ut så här:

7. Arbeta tillbaka nerifrån och upp. Vid det här laget, om du har gjort stegen rätt, är du halvvägs genom lösningen. Du måste ha den diagonala linjen med 1:or, med 0:or under den. Siffrorna i den fjärde kolumnen spelar ingen roll just nu. Nu arbetar du säkerhetskopiering enligt följande:

8. Kontrollera om du har skapat lösningsmatrisen. Om ditt arbete är korrekt har du skapat lösningsmatrisen med 1:or i en diagonal linje av R1C1, R2C2, R3C3 och 0:or i de andra positionerna i de tre första kolumnerna. Siffrorna i den fjärde kolumnen är lösningarna för ditt linjära system.
Del 3 av 4: Att sätta ihop stegen för att lösa systemet

1. Börja med ett exempelsystem av linjära ekvationer. För att öva på dessa steg, låt oss börja med systemet vi använde tidigare: 3x+y-z=9, 2x-2y+z=-3 och x+y+z=7. Om du skriver detta i en matris har du R1= [3.1,-1,9], R2=[2,-2,1,-3] och R3=[1,1,1,7].

2. Skapa en 1 i första positionen R1C1. Observera att R1 för närvarande börjar med en 3:a. Du måste ändra den till en 1. Du kan göra detta genom skalär multiplikation, genom att multiplicera alla fyra termerna av R1 med 1/3. I stenografi kan du skriva som R1*1/3. Detta ger ett nytt resultat för R1 om R1=[1,1/3,-1/3,3]. Använd R2 och R2, oförändrade, om R2=[2,-2,1,-3] och R3=[1,1,1,7].

3. Skapa en 0 i den andra raden, första kolumnen (R2C1). Vid denna punkt är R2=[2,-2,1,-3]. För att komma närmare lösningsmatrisen måste du ändra den första termen från en 2 till en 0. Du kan göra detta genom att subtrahera två gånger värdet från R1, eftersom R1 börjar med en 1. I stenografi är operationen R2-2*R1. Kom ihåg att du inte ändrar R1, bara arbeta med den. Så kopiera först R1 om R1=[1,1/3,-1/3,3]. Om du sedan dubblar varje term av R1 får du 2*R1=[2,2/3,-2/3,6]. Slutligen, subtrahera detta resultat från den ursprungliga R2 för att få din nya R2. Arbetar term för term, denna subtraktion blir (2-2), (-2-2/3), (1-(-2/3), (-3-6). Vi förenklar detta till nya R2=[0,-8/3,5/3,-9]. Observera att den första termen är 0 (oavsett vad ditt mål var).

4. Skapa en 1:a i andra raden, andra kolumnen (R2C2). För att fortsätta att bilda den diagonala linjen för 1:or måste du konvertera den andra termen -8/3 till 1. Gör detta genom att multiplicera hela raden med det reciproka talet (-3/8). Symboliskt är detta steg R2*(-3/8). Den resulterande andra raden är R2=[0.1,-5/8.27/8].

5. Skapa en nolla i den tredje raden, första kolumnen (R3C1). Ditt fokus flyttas nu till den tredje raden, R3=[1,1,1,7]. För att göra en 0 i den första positionen måste du subtrahera en 1 från 1:an i den positionen. Om du tittar upp, finns det en 1 i första positionen av R1. Så du behöver bara subtrahera R1 från R3 för att få det resultat du behöver. Arbetsperiod för termin blir detta (1-1), (1-1/3), (1-(-1/3)), (7-3). Dessa fyra miniproblem kan sedan förenklas till nya R3=[0.2/3.4/3.4].

6. Gör en nolla i tredje raden, andra kolumnen (R3C2). Detta värde är för närvarande 2/3, men måste konverteras till en 0. Vid första anblicken ser det ut som att du kan göra dubbelsubtraktion av R1-värdena, eftersom motsvarande kolumn i R1 innehåller en 1/3. Men om du dubblar och subtraherar alla värden på R1 ändras nollan i den första kolumnen i R3, vilket du inte vill ha. Detta skulle vara ett steg tillbaka i din lösning. Så du måste arbeta med någon kombination av R2. Om du subtraherar 2/3 från R2 skapar du en nolla i den andra kolumnen, utan att ändra den första kolumnen. I förkortad form är detta R3- 2/3*R2. De individuella termerna blir (0-0), (2/3-2/3), (4/3-(-5/3*2/3)), (4-27/8*2/3). Förenkling ger då R3=[0,0,42/24.42/24].

7. Skapa en 1:a i tredje raden, tredje kolumnen (R3C3). Detta är en enkel multiplikation med det reciproka talet som står. Det aktuella värdet är 42/24, så du kan multiplicera med 24/42 för att få önskat värde på 1. Observera att de två första termerna båda är 0, så all multiplikation förblir 0. Det nya värdet på R3=[0,0,1,1].

8. Skapa en nolla i den andra raden, tredje kolumnen. R2 är för närvarande [0,1,-5/8,27/8], med ett värde på -5/8 i den tredje kolumnen. Du måste omvandla det till en 0. Det betyder att du måste utföra någon operation med R3 som består av att lägga till 5/8. Eftersom den motsvarande tredje kolumnen i R3 är en 1, måste du multiplicera alla värden för R3 med 5/8 och lägga till resultatet till R2. Kort sagt är detta R2+5/8*R3. Term för term är detta R2=(0+0), (1+0), (-5/8+5/8), (27/8+5/8). Detta kan förenklas till R2=[0,1,0,4].

9. Skapa en nolla i första raden, tredje kolumnen (R1C3). Den första raden är för närvarande R1=[1.1/3,-1/3.3]. Du måste konvertera -1/3 i den tredje kolumnen till en 0, med någon kombination av R3. Du vill inte använda R2, eftersom 1:an i den andra kolumnen i R2 skulle modifiera R1 på fel sätt. Så du multiplicerar R3*1/3 och adderar resultatet till R1. Notationen för detta är R1+1/3*R3. Att räkna ut det term för term resulterar i R1=(1+0), (1/3+0), (-1/3+1/3), (3+1/3). Du kan förenkla detta till en ny R1=[1,1/3,0,10/3].

10. Gör en nolla i första raden, andra kolumnen (R1C2). Om allt görs rätt bör detta vara det sista steget. Du måste konvertera 1/3 i den andra kolumnen till en 0. Du kan få detta genom att multiplicera och subtrahera R2*1/3. Kort sagt är detta R1-1/3*R2. Resultatet är R1=(1-0), (1/3-1/3), (0-0), (10/3-4/3). Att förenkla ger då R1=[1,0,0,2].

11. Sök efter lösningsmatrisen. Vid det här laget, om allt gick bra, skulle du ha de tre raderna R1=[1,0,0,2], R2=[0,1,0,4] och R3=[0,0,1,1] måste ha. Observera att om du skriver detta i blockmatrisform med raderna ovanpå varandra, har du diagonala 1:or med 0:or längre fram, och dina lösningar finns i den fjärde kolumnen. Lösningsmatrisen ska se ut så här:

12. Förstår din lösning. När du har omvandlat de linjära ekvationerna till en matris, sätt in x-koefficienterna i den första kolumnen, y-koefficienterna i den andra kolumnen, z-koefficienterna i den tredje kolumnen. Om du nu vill skriva om matrisen till ekvationer betyder dessa tre rader i matrisen faktiskt de tre ekvationerna 1x+0y+0z=2, 0x+1y+0z=4 och 0x+0y+1z=1. Eftersom vi kan stryka över 0-ledarna och inte behöver skriva 1-koefficienterna, förenklas dessa tre ekvationer till lösningen, x=2, y=4 och z=1. Detta är lösningen på ditt linjära ekvationssystem.
Del 4 av 4: Kontrollera din lösning

1. Bearbeta lösningarna i varje variabel i varje ekvation. Det är alltid en bra idé att kontrollera om din lösning faktiskt är korrekt. Det gör du genom att testa dina resultat i de ursprungliga ekvationerna.
- De ursprungliga ekvationerna för detta problem var: 3x+y-z=9, 2x-2y+z=-3 och x+y+z=7. När du ersätter variablerna med deras värden du hittade får du 3*2+4-1=9, 2*2-2*4+1=-3 och 2+4+1=7.

2. Förenkla vilken ekvation som helst. Utför operationerna i varje ekvation enligt de grundläggande reglerna för operationer. Den första ekvationen förenklas till 6+4-1=9, eller 9=9. Den andra ekvationen kan förenklas till 4-8+1=-3, eller -3=-3. Den sista ekvationen är helt enkelt 7=7.

3. Skriv ner dina slutliga lösningar. För detta givna problem är den slutliga lösningen x=2, y=4 och z=1.
Tips
- Om ditt ekvationssystem är mycket komplext, med många variabler, kanske du vill använda en grafräknare istället för att göra arbetet för hand. För information om detta kan du också konsultera wikiHow.
Оцените, пожалуйста статью