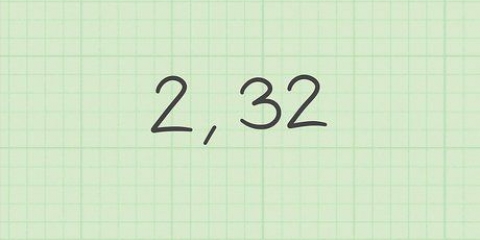Avrundande siffror

Steg
Tips
Varningar

Avrundning gör att tal har färre decimaler. Även om avrundade tal är mindre exakta än oavrundade tal, är de att föredra i många fall. Beroende på situationen kan det vara nödvändigt att avrunda decimaler eller heltal. Om du vill lära dig hur man avrundar tal, följ dessa steg.

Steg

Metod 1 av 3: Avrunda decimaler

1. Bestäm antalet decimaler för siffrorna efter decimalkomma, till vilken du måste avrunda talet. Detta kan bestämmas av din lärare, eller så kan du härleda det från sammanhanget och den typ av siffror du har att göra med. När det till exempel kommer till pengar vill du med största sannolikhet avrunda till hundradelen, eller till cent, medan du med en vikt behöver avrunda till gram.

Ju mindre exakt numret behöver vara, desto färre siffror efter decimalkomma.
Ju mer exakt, desto fler siffror efter decimalkomma.

2. Bestäm antalet siffror efter decimalkomma. Är numret 10,7659 givet och du vill runda av det till en tusendel, så kommer det att finnas 3 siffror efter decimalkomma. Ett annat tillvägagångssätt är att du avrundar siffran till 5 signifikanta siffror. Men lägg först märke till 5 av numret.

3. Hitta talet omedelbart till höger om talet som ska avrundas (5:an). Det är siffran 9. Detta nummer avgör om 5 är avrundad uppåt eller nedåt.

4. Runda upp siffran som ska avrundas (relevant siffra) om siffran till höger är 5, 6, 7, 8 eller 9. Detta kallas avrundning uppåt, eftersom talet du avrundar till är större än talet som ska avrundas uppåt. Den relevanta figuren 5, blir nu 6. Alla siffror till vänster om denna siffra förblir desamma, och siffrorna till höger försvinner (de spelar ingen roll längre, bara sätt dem lika med noll). Alltså antalet 10,7659 blir lika med efter avrundning till närmaste tusendel 10,766.

Även om 5:an är i mitten av siffrorna 1-9, siffran 5 behöver ett annat nummer för att avgöra hur det ska avrundas. Även om dina lärare inte alltid tillämpar detta när de betygsätter dig!

5. Runda ner en siffra om siffran till höger om den är 0, 1, 2, 3 eller 4. Det betyder för den aktuella siffran att den helt enkelt förblir densamma, även om detta kallas avrundning nedåt. Du kan aldrig ändra ett nummer till ett lägre nummer. Har du till exempel numret 10,7653, då skulle du avrunda detta till 10,765 eftersom betyget 3 på höger sida av 5 är mindre än 5.

Att lämna allt detsamma och sätta siffrorna till höger om den avrundade siffran till noll gör det slutliga talet mindre än originalet.

Metod 2 av 3: Avrundning av heltal

1. Avrunda ett tal till nästa tio. För att göra detta, titta på siffran till höger om tio. Tian är den andra siffran, sett från höger till vänster, i ett nummer. (Ta 12, då är 1 tion.) Sedan, om siffran är mellan 0-4, lämnar du siffran att avrunda oförändrad; om det är mellan 5-9, avrunda uppåt detta nummer 1. Här är några exempel:

12 --> 10
114 --> 110
57 --> 60
1 334 --> 1330
1,488 --> 1490
97--> 100

2. Avrunda ett tal till nästa hundratal. Följ samma protokoll som tidigare med tio. Kontrollera hundra, den tredje siffran i ett nummer, till vänster om tio. (I nummer 1.234, 2 är hundra). Använd sedan talet till höger om hundra, tiotalet, för att avgöra om du ska avrunda uppåt eller nedåt, med siffrorna efter lika med noll. Här är några exempel:

7.891 -- > 7.900

15.753 --> 15.800

99. 961 --> 100.000

3.350 --> 3.300

450 --> 500

3. Avrunda ett tal till nästa tusental. Samma regler gäller här igen. Hitta tusentalet och kontrollera sedan hundratalet innan du avrundar. Om talet är mellan 0-4, avrunda nedåt, och om det är mellan 5-9, avrunda uppåt. Här är några fler exempel:

8.800 --> 9.000

1.015 --> 1.000

12.450 --> 12.000

333.878 --> 334.000

400.400 --> 400.000

Metod 3 av 3: Avrunda tal till signifikanta siffror

1. Försök förstå vad ett betydande antal är. Betrakta en betydande siffra som en "intressant" eller a "Viktig" nummer som ger användbar information om ett nummer. Detta innebär att alla nollor till höger om heltal eller till vänster om decimaler kan utelämnas eftersom de bara fyller upp utrymmet. För att hitta antalet signifikanta siffror i ett tal, räkna helt enkelt antalet siffror från vänster till höger. Här är några exempel:

1 239 har 4 signifikanta siffror
134,9 har 4 signifikanta siffror
0,0165 har 3 signifikanta siffror

2. Avrunda ett tal till ett antal signifikanta siffror. Detta beror på vilket uppdrag du arbetar med. Till exempel, om du avrundar ett tal till två signifikanta siffror, bör du försöka känna igen den andra signifikanta siffran i numret och sedan använda siffran till höger för att avgöra om du ska avrunda uppåt eller nedåt. Här är några exempel:

1,239 avrundat till 3 signifikanta siffror är 1,24. Detta är korrekt eftersom siffran till höger om den tredje siffran (3) är en 9 (mer än 5).

134,9 avrundat till 1 signifikant siffra är 100. Detta är korrekt eftersom siffran till höger om hundra (1) är en 3 (mindre än 5).

0.0165 avrundat till 2 signifikanta siffror är 0.017. Detta är korrekt eftersom den andra signifikanta siffran är lika med 6, och siffran till höger är en 5:a, så avrundning uppåt.

3. Avrunda till korrekt antal signifikanta siffror vid tillägg. För att göra detta är det nödvändigt att först addera de givna talen tillsammans. Hitta sedan talet med minst antal signifikanta siffror och runda av ditt svar till det numret. Så här fungerar det:

13,214 + 234,6 + 7,0350 + 6,38=261,2290

Observera att den andra siffran, 234,6, bara är korrekt till en tiondel och har fyra signifikanta siffror.

Avrunda svaret så att svaret har samma noggrannhet, dvs till närmaste tiondel, eller till en decimal. 261,2290 blir sedan 261,2.

4. Avrunda till korrekt antal signifikanta siffror när du multiplicerar. Multiplicera först alla givna tal. Kontrollera sedan vilket av talen som avrundas till det minsta antalet signifikanta siffror. Slutligen, avrunda svaret med samma grad av noggrannhet som det numret. Så här fungerar det:

16,235 × 0,217 × 5=17,614975

Observera att siffran 5 bara har en signifikant siffra. Det betyder att det slutliga svaret bara kan ha en signifikant siffra.

17,614975 avrundat till en signifikant siffra blir sedan 20.

Tips

Det är vanligt att utelämna nollorna till höger om en decimal efter avrundning. Nollor till höger om en decimal ändrar inte värdet på talet. Det är därför de ska lämnas utanför. Detta gäller inte nollor till vänster om (före) en decimal.
När du har hittat det relevanta numret att avrunda, understryka det. Detta säkerställer att det inte finns någon förvirring om talet du ska avrunda och numret till vilket det relevanta numret avrundas.

Varningar

Se till att du är bekant med terminologin. Skillnaden mellan tiotals och tiondelar, hundratals och hundradelar, decimaler, decimaler, signifikans etc...