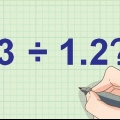Passar 15 till 34? Ja, visst, och så kan vi börja räkna ut svaret. (Den första siffran behöver inte passa perfekt, den måste bara vara mindre än den andra siffran). 
Vi måste lösa 34 ÷ 15, eller "hur många gånger går 15 in i 34"? Du letar efter ett tal som du kan multiplicera med 15 för att få ett tal som är mindre än 34, men ganska nära: Fungerar 1? 15 x 1 = 15, det är mindre än 34, men fortsätt att gissa. Fungerar 2? 15 x 2 = 30. Detta är fortfarande mindre än 34, så 2 är ett bättre svar än 1. Fungerar 3? 15 x 3 = 45, större än 34. För hög! Svaret är 2. 
Eftersom du beräknar 34 ÷ 15, skulle du skriva som svar, 2, på svarsraden ovanför "4". 
Ditt svar var 2 och det mindre talet i uppgiften är 15, så vi räknar ut 2 x 15 = 30. Skriv "30" under "34". 
Lös 34 – 30 och skriv svaret nedan på en ny rad. Svaret är 4. Denna 4 är fortfarande "resten" efter att ha dividerat 34 med 15 två gånger, så vi använder den i nästa steg. 
Lämna 4:an där den är och ta ner "7" från "3472" för att få 47. 
Vi löser: 47 ÷ 15: 47 är större än vårt senaste nummer, så svaret blir större. Låt oss prova fyra: 15 x 4 = 60. Nej, för stor! Istället försöker vi tre: 15 x 3 = 45. Mindre än 47 men nära det. Perfekt. Svaret är 3, så vi skriver det ovanför "7" på svarsraden. (Ska vi få en summa som 13 ÷ 15, där den första siffran är mindre, måste vi ta ner en tredje siffra innan vi kan lösa det). 
Kom ihåg att vi beräknade 47 ÷ 15 = 3 och vill nu hitta vad som är kvar: 3 x 15 = 45, så skriv "45" under 47. 47 - 45 = 2. Skriv "2" under 45. 
Nästa problem är 2 ÷ 15, vilket inte är så vettigt. Ta ner ett nummer för att göra det 22 ÷ 15. 15 går in i 22 en gång, så vi skriver `1` som den sista siffran i svaret. Vårt svar är nu 231. 
1 x 15 = 15, så skriv 15 under 22. Beräkna 22 - 15 = 7. Det finns inga fler tal att ta ner, så istället för att fortsätta dividera skriver vi `vila 7` efter vårt svar. Det slutliga svaret: 3472 ÷ 15 = 231 resterande 7.


Om du tycker att detta är svårt, räkna bara i tre exemplar och lägg till en nolla i slutet. Räkna tills du blir högre än det största numret i problemet (143), och sluta där. 
30 (ett finger), 60 (två fingrar), 90 (tre fingrar), 120 (fyra fingrar). Alltså 30x fyra = 120. 150 (fem fingrar), alltså 30 x fem = 150. 4 och 5 är de två mest troliga svaren på vårt problem. 
27 x 4 = 108 27 x 5 = 135 
27 x 6 = 162. Detta är högre än 143, så det kan inte vara rätt svar. 27 x 5 kom närmast utan att gå över, så 143 ÷ 27 = 5 (plus en rest 8, eftersom 143-135 = 8).
Dividera med ett tal med två eller fler siffror
Att dividera med ett tal med två eller fler siffror är väldigt likt lång division med en siffra, men det tar lite längre tid och kräver lite mer träning. Eftersom de flesta av oss inte kommer ihåg tabellen med 47, kräver det lite gissningar, men det finns ett snyggt trick du kan lära dig att göra det snabbare. Det blir också lättare med lite träning, så bli inte frustrerad om det verkar långsamt i början.
Steg
Del 1 av 2: Dividera med ett tvåsiffrigt tal

1. Titta på den första siffran i det större numret. Skriv problemet som långdivision. Som ett enklare divisionsproblem, tittar du i princip på det mindre talet och frågar dig själv: "Passar det in i den första siffran i det större talet??`
- Anta att du har problemet 3472 ÷ 15. Passar 15 i 3? Eftersom 15 definitivt är större än 3 är svaret "nej" och låt oss gå vidare till nästa steg.

2. Titta på de två första siffrorna. Eftersom ett tvåsiffrigt tal inte kan passa in i ett ensiffrigt tal, låt oss nu titta på två siffror, precis som vi skulle göra med ett vanligt divisionsproblem. Om det fortfarande är omöjligt att dela, måste du titta på de tre första siffrorna, men i vårt exempel är det inte nödvändigt:

3. Använd lite gissningar. Kontrollera hur många gånger den första siffran passar in i den andra. Du kanske redan vet svaret, men om inte, gör en uppskattning och kontrollera ditt svar med en multiplikation.

4. Skriv svaret ovanför den senaste siffran du använde. Att skriva det här som lång division borde kännas bekant.

5. Multiplicera ditt svar med det mindre talet. Detta är samma som vanlig långdivision, men här använder vi ett tvåsiffrigt tal.

6. Subtrahera båda siffrorna från varandra. Det sista du skrev gick under det ursprungliga större numret (eller en del av det). Behandla detta som en minussumma och skriv svaret under det på en ny rad.

7. Ta ner nästa nummer. Precis som ett vanligt divisionsproblem fortsätter vi att beräkna nästa siffra i svaret tills vi är klara.

8. Lös följande delproblem. För att få nästa nummer, upprepa samma steg som ovan för det nya problemet. Du kan gå tillbaka till att uppskatta för att hitta svaret:

9. Fortsätt med lång division. Upprepa lång division som vi gjorde tidigare för att multiplicera vårt svar med det mindre talet, skriv resultatet under det större talet och subtrahera dem för nästa återstod.

10. Bestäm den sista siffran. Som tidigare tar vi ner nästa siffra från det ursprungliga problemet så att vi kan lösa nästa delproblem. Upprepa stegen ovan tills du hittar varje siffra i svaret.

11. Bestäm resten. Nu bara en minussumma för att hitta den sista vilan, och vi är klara. Faktum är att om svaret på minussumman är 0, behöver du inte skriva en rest alls.

Del 2 av 2: Lär dig att uppskatta väl

1. Runda till närmaste tio. Det är inte alltid lätt att se hur många gånger ett tvåsiffrigt tal passar in i ett större tal. Ett användbart knep är att avrunda till närmaste multipel av 10 för att göra det lättare att gissa. Detta är användbart för mindre divisionsproblem eller lång division.
- Låt oss till exempel säga att vi måste lösa för 143 ÷ 27, men vi vet inte hur många gånger 27 går in i 143. Låt oss sedan låtsas att vi måste lösa 143 ÷ 30.

2. Räkna det mindre antalet på fingrarna. I vårt exempel kan vi börja räkna med 30 och inte med 27. Att räkna i steg om 30 är ganska enkelt när du väl har fått kläm på detta: 30, 60, 90, 120, 150.

3. Bestäm de två mest troliga svaren. Siffran passade inte riktigt in i 143, men vi vet siffror som är nära: 120 och 150. Låt oss se hur många fingrar vi måste räkna för att komma dit:

4. Testa dessa två siffror med det verkliga problemet. Nu när vi har två bra gissningar kan vi testa dem på det ursprungliga problemet, 143 ÷ 27:

5. Se till att du inte kan komma närmare. Eftersom båda talen slutar under 143, kan vi försöka komma ännu närmare genom att försöka ytterligare en multiplikation:

Tips
- Om du inte vill multiplicera för hand under lång division, försök dela upp problemet i siffror och lösa varje del utantill. Till exempel, 14 x 16 = (14 x 10) + (14 x 6). Skriv ner 14 x 10 = 140 så att du inte glömmer. Sedan: 14 x 6 = (10 x 6) + (4 x 6). 10 x 6 = 60 och 4 x 6 = 24. Gör 140 + 60 + 24 = 224 och du har svaret.
Varningar
- Om din minussumma vid något tillfälle resulterar i ett tal som är större än divisorn, så var din uppskattning inte tillräckligt hög. Radera hela steget och försök uppskatta större.
- Om din minussumma någon gång resulterade i en negativ antal, då var din uppskattning för hög. Radera hela steget och försök uppskatta mindre.
Andra resurser
"Dividera med ett tal med två eller fler siffror"
Оцените, пожалуйста статью