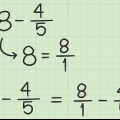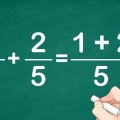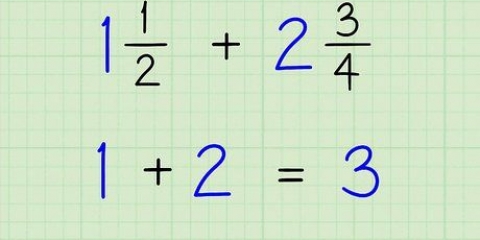Subtrahera siffror

Steg
Tips
Varningar

Subtraktioner är de summor där du subtraherar två tal från varandra. Det är ganska enkelt om du vill subtrahera heltal från varandra, men det blir lite mer komplicerat när du arbetar med bråk eller decimaler. När du har bemästrat subtraktion kan du gå vidare till de mer komplicerade matematiska begreppen och att lägga till, multiplicera och dividera siffror blir mycket lättare.

Steg

Metod 1 av 6: Subtrahera stora heltal genom att låna

1. Skriv ner det större numret. Anta att du arbetar med summan 32 - 17. Skriv ner 32 först.

2. Skriv det mindre numret direkt under det. Se till att tior och ettor är snyggt uppradade så att de 3 in "32" direkt över 1 tum "17" tillstånd och 2 tum "32" direkt ovanför "7" vid 17.

3. Subtrahera det nedersta numret från toppen. Detta kan bli lite knepigt om det nedre numret är större än det översta. I det här fallet är 7 större än 2. Så här gör du:

du måste "att låna" av de 3 tum "32" att göra 2 till 12.

Korsa 3 av "32" och gör det till en 2, gör sedan enheten 2 till en 12.

Nu har du 12 – 7 = 5. Skriv en 5:a under enhetskolumnen.

4. Subtrahera de tio i det nedersta numret från de tio i det översta talet. Glöm inte att 3:an av 32 har blivit en 2:a. Subtrahera nu 1 på 17 från 2 ovanför, så 2-1= 1. Skriv 1 under tiotalskolumnen. Om allt är bra har du nu 15 som svar, så 32 - 17 = 15.

5. Kontrollera ditt arbete. Om du vill vara säker på att du har gjort beräkningen korrekt behöver du bara lägga till svaret till det minsta talet för att få tillbaka det största talet. Så för att kontrollera: 15 + 17 = 32, så du gjorde det rätt. Excellent!

Metod 2 av 6: Subtrahera små heltal

1. Bestäm vilket nummer som är störst. En övning som 15 - 9 kräver ett annat tillvägagångssätt än 2 - 30.

I summan 15 - 9 är det första talet, 15, det största.
I summan 2 - 30, det andra talet, är 30 det största.

2. Bestäm om ditt svar ska vara positivt eller negativt. Om den första siffran är den största är svaret positivt. Om den andra siffran är den största är svaret negativt.

Så i den första summan, 15 - 9, blir svaret positivt, eftersom 15 är större än 9.

Så i den andra summan, 2 - 30, blir svaret negativt, eftersom 2 är mindre än 30.

3. Hitta skillnaden mellan de två siffrorna. För att subtrahera två tal, beräkna skillnaden mellan dem.

För uppgiften 15 - 9, ta 15 mynt. Ta bort 9 och räkna hur många som är kvar (6). Så, 15 - 9 = 6. Eller använd en sifferlinje och rita siffrorna 1 till 15 längs linjen, stryk sedan över 9 från 15 ner för att komma till 6.

Med summan 2 – 30 är det lättare att vända på siffrorna och göra svaret negativt. Så, 30 - 2 = 28, och med det är 2 - 30 -28.

Metod 3 av 6: Subtrahera decimaler

1. Skriv det större talet ovanför det mindre så att decimalerna är i linje. Anta att du har följande problem: 10.5 - 8.3. Skriv 10,5 ovanför 8,3 på ett sådant sätt att kommatecken är ovanför varandra.

Om du har ett problem där ett nummer har fler decimaler än det andra, fyll det tomma utrymmet med nollor. Om du till exempel har problemet 5.32 - 4.2 kan du skriva om det till 5.32 = 4.20. Detta ändrar inte värdet på ett tal, men du ser till att båda talen lättare kan subtraheras från varandra.

2. Subtrahera tiondelarna från varandra. Subtraktion från dessa siffror är samma som med heltal, förutom att du måste vara uppmärksam på decimalkomma, justerad och inkluderad i svaret. I det här fallet måste du subtrahera 3 från 5. 5 - 3 = 2, så du skriver en 2:a under 3:an i 8.3.

Glöm inte att inkludera decimaltecknet (kommet) i svaret. Det ser nu ut så här: ,2.

3. Subtrahera nu enheterna från varandra. Subtrahera nu 8 från 0. Låna ett dussin av 1:an (bredvid 0:an) för att göra 10, subtrahera nu 8 från 10. Du kan också omedelbart beräkna summan 10 – 8 = 2, utan det mellanliggande steget att låna, eftersom det nedersta talet inte har en tio. Skriv svaret under 8.

4. Så det slutliga svaret blir 2,2.

Metod 4 av 6: Subtrahera fraktioner

1. Sätt ihop täljare och nämnare. Anta att du arbetar med problemet 13/10 - 3/5. Skriv detta problem så att båda täljarna, 13 och 3, och båda nämnarna, 10 och 5, ligger bredvid varandra, åtskilda av ett minustecken. Detta ger dig en bättre överblick över problemet och gör det lättare att hitta en lösning.

2. Hitta den minsta gemensamma multipeln. Detta är den minsta multipeln av två tal. LCF för 10 och 5 i detta exempel är 10.

Observera att lcm för två siffror inte alltid är ett av de två talen. Till exempel, vid 3 och 2 är LCF 6, eftersom det inte finns ett tal mindre än 6 som är en multipel av vart och ett av talen.

3. Skriv om bråken med samma nämnare. Bråket 13/10 kan förbli oförändrat eftersom nämnaren inte har ändrats, men bråket 3/5 blir lika med 6/10 eftersom nämnaren går två gånger in i den gemensamma multipeln av 10. Nu har du utjämnat båda bråken. 3/5 är lika med 6/10, men med skillnaden att det nu inte längre är ett problem att subtrahera båda bråken från varandra.

Så den nya uppgiften blir: 13/10 - 6/10.

4. Subtrahera båda täljarna från varandra. Så 13 - 6 = 7. Subtrahera inte nämnare.

5. Placera den nya täljaren ovanför den nya nämnaren (den tidigare beräknade LCF) för det slutliga svaret. Den nya täljaren är 7 och nämnaren för båda bråken är 10. Så det slutliga svaret är 7/10.

6. Kontrollera ditt arbete. Om du vill vara säker på att du har gjort beräkningen korrekt behöver du bara lägga till svaret till det minsta talet för att få tillbaka det största talet. Så för att kontrollera: 7/10 + 6/10 = 13/10. Nu är du redo.

Metod 5 av 6: Subtrahera ett bråktal från ett heltal

1. Skriv uppgiften. Anta att vi har följande problem: 5 - 3/4. Notera detta.

2. Konvertera hela talet till ett bråk med samma nämnare som det givna bråket. Gör en bråkdel av 5:an med nämnaren 4. Tänk först på att 5 är lika med bråket 5/1. Sedan multiplicerar du både täljaren och nämnaren för det nya bråket med 4 för att få två bråk med samma nämnare. Detta håller värdet på bråket detsamma, men med olika tal. Så, 5/1 x 4/4 = 20/4.

3. Skriv om uppgiften. Detta kan nu skrivas som: 20/4 - 3/4.

4. Subtrahera täljarna för bråken och håll bråken lika. Så, 20 - 3 = 17. Så den slutliga täljaren blir 17 och nämnaren är 4.

5. Så svaret på problemet är 17/4. För att omvandla denna oegentliga fraktion till en sammansatt fraktion, dividera 17 med 4 för att få talet 4 med resten av 1. Svaret ser då ut så här: 4 1/4.

Metod 6 av 6: Subtrahera variabler

1. Skriv uppgiften. Anta att du arbetar med följande problem: 3x - 5x + 2y - z - (2x + 2x + y). Skriv den första ekvationen ovanför den andra.

2. Subtrahera alla liknande termer från varandra. När du arbetar med variabler kan du bara subtrahera termer med samma variabel och med samma kraft. Det betyder att du kan göra 4x -7x, men inte 4x -7x. Så du kan dela upp den här uppgiften så här:

3x - 2x = x

-5x - 2x = -7x

2y - y = y

-z - 0 = -z

3. Ge ditt slutliga svar. Nu när du har subtraherat alla lika termer kan du genast ge ditt slutliga svar. Här är svaret:

3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Tips

Dela större antal i mindre bitar. Tar: 63 - 25.Ingen säger att du måste subtrahera alla 25 på en gång. Du kan först subtrahera 3 för att få 60; subtrahera sedan 20 för att få 40 och sedan de sista 2. Resultat: 38. Och nu behöver du inte låna.