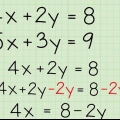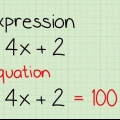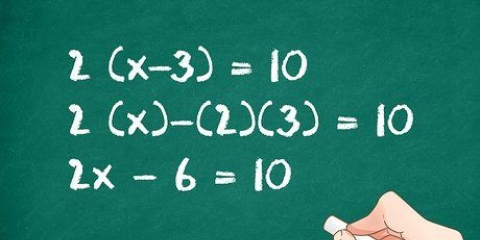Anta till exempel att du har ekvationen 3X + -2X + 14X=0. Av a X utanför parentes, får vi X(3X + -2X + 14)=0. 
I vårt exempeluttalande fyller vi i våra värderingar a, b och c (3, -2 respektive 14) i andragradsekvationen i: Svar 1: Svar 2: 
Anledningen till att detta fungerar har att göra med det grundläggande faktum att vilket tal som helst multiplicerat med noll är lika med noll. När du konverterar ekvationen till formen X(yxa + bx + c)=0, du delar i huvudsak de två i delar: en del är X-variabel utanför parentes och den andra är kvadraten inom parentes. Om någon av dessa delar är lika med noll, så är hela ekvationen det också. Så om de två svaren på kvadraten inom parentesen gör den delen till noll, så kommer svaren på kubikekvationen också att göra delen utanför parentesen lika med noll. 

I vårt exempeluttalande, a=2 och d=6. Faktorerna för 2 är 1 och 2. Faktorerna 6 är 1, 2, 3 och 6. 
I vår ekvation beräknar du faktorerna för a (1, 2) på faktorerna d (1, 2, 3, 6) och du får följande lista: 1, 1/2, 1/3, 1/6, 2 och 2/3. Nu lägger vi till de negativa talen till listan för att göra den komplett: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 och -2/3. Heltalslösningen för vår kubikekvation kan hittas någonstans i den här listan. 
Syntetisk delning är ett komplext ämne — följ länken ovan för mer information. Här är ett exempel på att hitta en av lösningarna till vår kubikekvation med hjälp av syntetisk division: 

I vårt exempelproblem löser vi detta på följande sätt: 
I vårt exempelproblem löser vi detta på följande sätt: 
I vårt exempelproblem är det mycket enkelt att bestämma Δ, eftersom både Δ0 och Δ1=0. Vi löser detta på följande sätt: 
I vårt exempelproblem hittar vi C som följer: 
I vårt exempelproblem kan vi lösa detta genom att kontrollera svaret när n är lika med 1, 2 eller 3. Svaren vi får från dessa tester är de möjliga svaren på vår kubikekvation - varje lösning som ger 0 efter substitution i ekvationen är korrekt. Anta till exempel att vi får 1 som svar på ett av testerna, eftersom anger 1 in X - 3X + 3X - 1 ger 0 om svar, alltså 1 ett av svaren på vår kubikekvation.
Lösa en kubikekvation
Första gången du stöter på en kubikekvation (av formen yxa + bx + cx + d=0) det kan se nästan olösligt ut. Denna metod för att lösa kubiska ekvationer har dock funnits i århundraden! Den upptäcktes på 1500-talet av de italienska matematikerna Niccolò Tartaglia och Gerolamo Cardano. Det var en av de första formlerna som var okända för de gamla grekerna och romarna. Att lösa kubikekvationer kan vara mycket svårt, men med rätt tillvägagångssätt (och tillräckligt med grundläggande kunskaper) kan även de knepigaste kubikekvationerna tämjas.
Steg
Metod 1 av 3: Lös det med abc-formeln

1. Kontrollera om kubikekvationen innehåller en konstant. Som anges ovan har kubiska ekvationer formen yxa + bx + cx + d=0. före Kristus, och d kan vara 0 utan att ändra om det är en kubikekvation eller inte - vilket i huvudsak betyder att en ekvation inte behöver bestå av alla termer bx, cx eller d vara en kubikekvation. Du börjar tillämpa denna relativt enkla metod för att lösa kubiska ekvationer genom att först kontrollera om din ekvation har en konstant (en d-där den). Är detta inte fallet, då kan du de abc formel att hitta svaren på ekvationen med lite matematik.
- Om ekvationen innehåller en konstant måste du använda en annan metod. Se nedan för alternativa tillvägagångssätt.

2. lösa upp a X ur ekvationen. Eftersom din ekvation inte innehåller en konstant, har varje term i ekvationen en X-variabel. Detta innebär att a X kan tas ut ur ekvationen för att förenkla den. Gör detta och skriv om din ekvation i formuläret X(yxa + bx + c).

3. Använd abc-formeln för att lösa termerna inom parentes. Du kanske har märkt att termerna för din nya ekvation inom parentes är i form av en andragradsekvation (yxa + bx + c). Det betyder att vi kan hitta de värden för vilka andragradsekvationen är lika med noll med a, b och c i abc-formeln ({-b +/-√ (b- 4ac)}/2a). Detta kommer att hitta två av svaren i din kubikekvation.
- {-b +/-√ (b- 4ac)}/2a
- {-(-2) +/-√ ((-2)-4(3)(14))}/2(3)
- {2 +/-√ (4 - (12)(14))}/6
- {2 +/-√ (4 - (168)}/6
- {2 +/-√ (-164)}/6
- {2 + √(-164)}/6
- {2 + 12.8i}/6
- {2–12.8i}/6

4. Använd noll och andragradssvaren som svar på din kubikekvation. Fyrkantsekvationer har två lösningar, men kubiska ekvationer har tre. Du har redan två — det här är svaren du hittade genom att räkna ut den "kvadratiska ekvationen" inom parentes. I de fall där en ekvation är lämplig för denna "utanför parentes", kommer det tredje svaret alltid att vara 0 är. Grattis — du har precis löst en kubikekvation.
Metod 2 av 3: Lösning med hjälp av faktorlistor

1. Se till att din kubikekvation har en konstant. Även om metoden ovan är användbar eftersom den inte kräver att du lär dig nya matematiska färdigheter, fungerar den inte alltid för att lösa kubikekvationer. Om din ekvation är i formen yxa + bx + cx + d=0 tillstånd, och d är icke-noll, kommer parenteserna inte att fungera, och du behöver antingen den här metoden eller den i nästa del.
- Anta till exempel att du har den givna ekvationen 2X + 9X + 13X=-6. I det här fallet kommer en 0 till höger om likhetstecknet att kräva att man lägger till 6 på båda sidor. Vår nya ekvation är 2X + 9X + 13X + 6=0, d=6, så vi kan inte använda parenteserna från föregående del.

2. Bestäm faktorerna för a och d. För att lösa kubikekvationen, börja med att bestämma faktorerna för a (koefficienten för X villkor d (konstanten i slutet av ekvationen). Som en påminnelse är faktorer de tal som multiplicerats tillsammans bildar ett annat tal. Till exempel för att din 6 kommer från multiplikationen 6 &tid; 1 och 2 × 3, är 1, 2, 3 och 6 faktorer av 6.

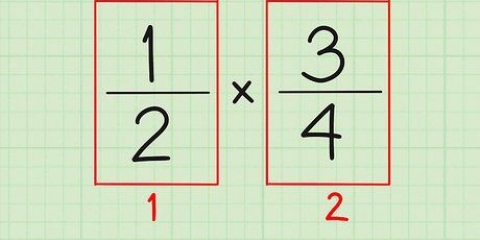
3. Dela faktorerna för a av faktorerna d. Nu listar du alla värden du får genom att dividera varje faktor a av någon faktor d. Detta resulterar vanligtvis i många bråk och några få heltal. Heltalslösningarna i din kubikekvation kommer att vara antingen ett av heltal från listan eller det negativa talet för ett av dessa tal.

4. Använd syntetisk delning för att manuellt kontrollera dina svar. När du har satt ihop värdelistan kan du hitta heltalslösningarna till din kubikekvation genom att snabbt manuellt mata in varje heltal och kontrollera vilka som är lika med noll. Vill man inte lägga tid på detta så finns det en lite snabbare metod enl en teknik som kallas syntetisk delning. Kontentan är att du dividerar heltal med originalet a, b, c och d koefficienter för din kubikekvation. Om du står kvar med en återstod av 0, är ditt värde en av lösningarna till kubikekvationen.
- -1 | 2 9 13 6
- __| -2-7-6
- __| 2 7 6 0
- Eftersom vi slutar med en 0 som rest, vet vi att en av lösningarna till vår kubikekvation är heltal -1 är.
Metod 3 av 3: Använda "diskriminanten"

1. Skriv ut värdena för a, b, c och d. I den här metoden för att hitta lösningarna till en kubikekvation kommer vi att förlita oss mycket på koefficienterna för termerna i vår ekvation. Av denna anledning är det klokt att använda termerna a, b, c och d skriv ner det innan du börjar så att du inte glömmer vad var och en är.
- Till exempel för jämförelsen X - 3X + 3X - 1, skriver vi a=1, b=-3, c=3 och d=-1. Glöm inte det av a X-variabel utan koefficient antas att koefficienten är lika med 1.

2. Beräkna Δ0=b - 3ac. När du använder diskriminanten för att lösa kubikekvationer behöver du lite mer avancerad matematik, men om du följer proceduren noggrant kommer du att tycka att det är ett värdefullt verktyg för att lösa de redan knepiga kubikekvationerna. Börja med att hitta Δ0, det första av flera viktiga värden vi behöver, genom att ersätta de lämpliga värdena i formeln b - 3ac.
- b - 3ac
- (-3) - 3(1)(3)
- 9 - 3(1)(3)
- 9 - 9=0=A0

3. Beräkna Δ1=2b - 9ABC + 27ad. Nästa viktiga kvantitet vi behöver, Δ1, kräver lite mer arbete, men kan hittas på ungefär samma sätt som Δ0. Ersätt de korrekta värdena i formel 2b - 9ABC + 27ad för värdet av Δ1.
- 2(-3) - 9(1)(-3)(3) + 27(1)(-1)
- 2(-27) - 9(-9) + 27(-1)
- -54 + 81 - 27
- 81 - 81=0=Δ1

4. Beräkna Δ=Δ1 - 4Δ0) ÷ -27a. Sedan beräknar vi diskriminerande av kubikekvationen från värdena för Δ0 och Δ1. En diskriminant är helt enkelt ett tal som säger oss något om svaren på ett polynom (omedvetet kanske du redan känner till den kvadratiska diskriminanten: b - 4ac). När det gäller kubikekvationen, om diskriminanten är positiv, så har ekvationen tre reella lösningar. Om diskriminanten är noll, har ekvationen en eller två reella lösningar, och några av dessa lösningar är delade. Om den är negativ har ekvationen bara en lösning. (En kubikekvation har alltid en verklig lösning, eftersom grafen alltid är minst en gång med X-axelskärningar.)
- Δ1 - 4Δ0) ÷ -27a
- (0) - 4(0)) -27(1)
- 0 - 0 27
- 0=Δ, så vår ekvation har 1 eller 2 svar.

5. Beräkna C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). Det sista viktiga värdet att beräkna är C. Med denna viktiga kvantitet kan vi äntligen hitta de tre lösningarna. Lös detta som vanligt, ersätt Δ1 och Δ0 vid behov.
- √(√((Δ1 - 4Δ0) + Δ1)/ 2)
- √(√((0 - 4(0)) + (0))/ 2)
- √(√((0 - 0) + (0))/ 2)
- 0=C

6. Beräkna de tre svaren med dina variabler. Svaren på din kubikekvation ges av formeln (b + uC + (Δ0/uC)) / 3a, varigenom du=(-1 + √(-3))/2 och n är 1, 2 eller 3. Ange dina värden där det behövs för att lösa detta - detta kräver mycket matematik, men bör ge dig tre möjliga svar!
Оцените, пожалуйста статью