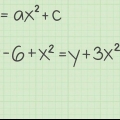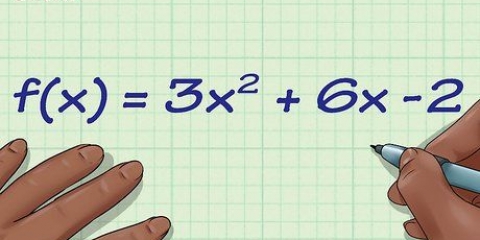Kom ihåg att varje operation på ena sidan av likhetstecknet också måste göras på den andra sidan. Exempel: För att fortsätta med vårt exempel lägger vi först till 2 på båda sidor av ekvationen. Detta ger oss y + 2 = 5x. Sedan dividerar vi båda sidor av ekvationen med 5 och lämnar (y + 2)/5 = x. Slutligen, för att göra det mer läsbart, skriver vi om ekvationen med "X" till vänster: x = (y + 2)/5. 
Exempel: Efter att ha bytt x och y får vi y = (x + 2)/5 
Eftersom X är lika med 1/x kan du också skriva f(x) som "1/f(x)," en annan notation för inversen av f(x). 
Exempel: Låt oss ange 4 som värdet på X i vår ursprungliga jämförelse. Detta ger oss f(x) = 5(4) - 2, eller f(x) = 18. Därefter ska vi lägga in detta resultat i det omvända. Så vi ersätter 18 i den inversa funktionen som värdet av X. Genom att göra detta får vi y = (18 + 2)/5 som ett resultat och detta är lika med y = 4. Så 4 är x-värdet vi började med och med det vet vi att vi har hittat rätt invers funktion.
Hitta inversen av en funktion
En funktion i matematik (vanligtvis noterad som f(x)) kan ses som en sorts formel eller program där du anger ett värde "X" tucks in, som sedan returnerar ett givet värde för y. De omvänd av en funktion f(x) (noterad som f(x)) är i huvudsak det omvända: skriv in a y-värde och du får desto tidigare X-värde tillbaka. Att hitta inversen av en funktion kan verka komplicerat, men för enkla ekvationer behöver du bara lite kunskap om de grundläggande operationerna i algebra. Läs följande steg-för-steg-instruktioner och ta en ordentlig titt på exemplet.
Steg

1. Skriv din funktion genom att byta ut f(x) med y om nödvändigt. Din formel hör hemma y att ha på ena sidan av likhetstecknet och på andra sidan X-villkor. Om du redan har skrivit in en ekvation y och X termer (som till exempel 2 + y = 3x), då behöver du bara y lösas genom att isolera den.
- Exempel: Vi har en funktion f(x) = 5x - 2, och skriver om den som y = 5x - 2, helt enkelt genom "f(x)" att ersättas av y.
- Notera: f(x) är standardfunktionsbeteckningen, men om du har att göra med flera funktioner kommer varje funktion att ges en annan initialbokstav för att göra det lättare att särskilja dem. Till exempel är g(x) och h(x) vanliga bokstäver för funktioner.

2. lösa X på. Med andra ord, gör de nödvändiga ändringarna X att isolera på ena sidan av likhetstecknet. För att göra detta, använd de grundläggande funktionerna i algebra: if X har en koefficient (ett tal för variabeln), dividera båda sidor av ekvationen med detta tal för att ta bort det; finns det en konstant inom "X"-term, räkna sedan ut det genom att addera eller subtrahera båda sidorna av likhetstecknet, och så vidare.

3. Byt variabler. Byta X av y och vice versa. Den resulterande ekvationen är inversen av den ursprungliga funktionen. Med andra ord, om vi har ett värde för X fyll i vår ursprungliga ekvation, så kan vi fylla i svaret i inversen (igen för "X") som returnerar det ursprungliga värdet!

4. byta ut y medelst "f(x)". Inversa funktioner noteras vanligtvis som f(x) = (x termer) . Kom ihåg att i det här fallet betyder exponenten -1 inte att vi måste utföra en exponentiell operation på funktionen. Det är bara ett sätt att indikera att denna funktion är inversen av originalet.

5. Kontrollera ditt arbete. Försök att fylla i en konstant i den ursprungliga funktionen för X. Om du hittade den korrekta inversen skulle du hitta det ursprungliga värdet på "X" bör se det igen, om du anger resultatet av detta i inversen.
Tips
- Du kan använda båda beteckningarna f(x) = y och f^(-1)(x) = y utan problem om du gör matematiska operationer på funktionerna. Men det är bättre att hålla isär den ursprungliga funktionen och den omvända funktionen, så försök att hålla den i gemensam notation. I fallet med den inversa funktionen notationen f^(-1)(x).
- Observera att inversen av en funktion vanligtvis, men inte alltid, är en funktion i sig.
"Hitta inversen av en funktion"
Оцените, пожалуйста статью