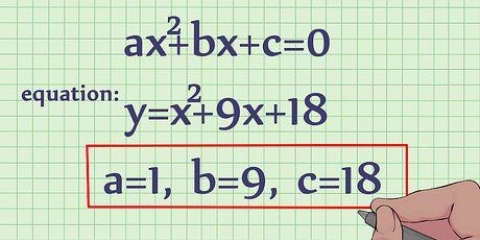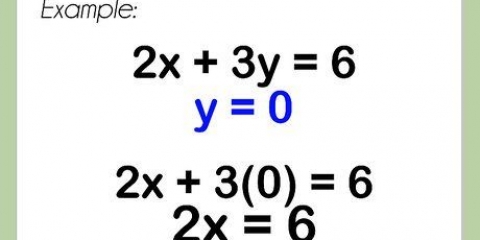Ta exempeljämförelsen  , där y-termerna kan flyttas åt vänster genom att subtrahera ett y från båda sidor. De andra termerna kan flyttas till höger sida genom att lägga till 6 på båda sidor och
, där y-termerna kan flyttas åt vänster genom att subtrahera ett y från båda sidor. De andra termerna kan flyttas till höger sida genom att lägga till 6 på båda sidor och  att dra av från båda sidor. Den resulterande ekvationen är
att dra av från båda sidor. Den resulterande ekvationen är  .
. 
Se exempeljämförelsen  . Det finns ingen begränsning för de tillåtna värdena för x för denna ekvation. Du måste dock inse att detta är ekvationen för en parabel, med x=0 som centrum, och en parabel är inte en funktion eftersom det inte är en en-till-en jämförelse av x- och y-värden. För att begränsa denna ekvation och göra den till en funktion, för vilken vi kan hitta en invers, måste vi definiera domänen som x≥0.
. Det finns ingen begränsning för de tillåtna värdena för x för denna ekvation. Du måste dock inse att detta är ekvationen för en parabel, med x=0 som centrum, och en parabel är inte en funktion eftersom det inte är en en-till-en jämförelse av x- och y-värden. För att begränsa denna ekvation och göra den till en funktion, för vilken vi kan hitta en invers, måste vi definiera domänen som x≥0. Utbudet är begränsat på samma sätt. Observera att den första termen,  , kommer alltid att vara positiv eller 0, för valfritt värde på x. Om ekvationen sedan adderar +2, kommer intervallet att vara vilket värde som helst y≥2.
, kommer alltid att vara positiv eller 0, för valfritt värde på x. Om ekvationen sedan adderar +2, kommer intervallet att vara vilket värde som helst y≥2. Det är nödvändigt att definiera domänen och omfattningen i detta tidiga skede. Du kommer att använda dessa definitioner senare när du definierar domänen och omfattningen av den inversa funktionen. Faktum är att domänen för den ursprungliga funktionen blir området för den inversa funktionen, och området för den ursprungliga funktionen blir domänen för den inversa. 
Arbetar med exempeljämförelsen  , detta inversionssteg kommer att resultera i den nya ekvationen av
, detta inversionssteg kommer att resultera i den nya ekvationen av  .
. Ett alternativt format är att ersätta y-termerna med x, men ersätta x-termerna med någondera  eller
eller  för att indikera den inversa funktionen.
för att indikera den inversa funktionen. 
 (ursprunglig premiss)
(ursprunglig premiss) (subtrahera 2 från båda sidor)
(subtrahera 2 från båda sidor) (diva båda sidor med 2)
(diva båda sidor med 2)± (kvadratroten från båda sidor; kom ihåg att kvadratroten resulterar i både positiva och negativa möjliga svar)
(kvadratroten från båda sidor; kom ihåg att kvadratroten resulterar i både positiva och negativa möjliga svar) 
Se lösningen av exempelekvationen ± . Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara
. Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara  var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥2. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥0, om du tar den positiva lösningen av kvadratroten, eller y≤0, om du tar den negativa lösningen av kvadratroten. Observera att för att hitta den inversa funktionen definierade du ursprungligen domänen som x≥0. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet.
var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥2. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥0, om du tar den positiva lösningen av kvadratroten, eller y≤0, om du tar den negativa lösningen av kvadratroten. Observera att för att hitta den inversa funktionen definierade du ursprungligen domänen som x≥0. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet. Jämför domänen och intervallet för inversen med originalets domän och intervall. Kom ihåg det för den ursprungliga funktionen,  , domänen definierades som alla värden på x≥0, och intervallet definierades som alla värden på y≥2. För den inversa funktionen byter nu dessa värden, och domänen är alla värden på x≥2, och intervallet är alla värden på y≥0.
, domänen definierades som alla värden på x≥0, och intervallet definierades som alla värden på y≥2. För den inversa funktionen byter nu dessa värden, och domänen är alla värden på x≥2, och intervallet är alla värden på y≥0. 
Som ett exempel, välj värdet x=1 för den ursprungliga ekvationen  . Detta ger resultatet y=4.
. Detta ger resultatet y=4. Sedan sätter du värdet 4 i den inversa funktionen  . Detta ger verkligen resultatet y=1. Du kan dra slutsatsen att din inversa funktion är korrekt.
. Detta ger verkligen resultatet y=1. Du kan dra slutsatsen att din inversa funktion är korrekt. 

Observera att denna standardform består av en perfekt kvadratisk term,  , som sedan modifieras av de andra två elementen a och k. För att komma fram till denna perfekta andragradsform måste du skapa vissa villkor i din andragradsekvation.
, som sedan modifieras av de andra två elementen a och k. För att komma fram till denna perfekta andragradsform måste du skapa vissa villkor i din andragradsekvation. 
För att slutföra kvadraten, arbeta bakåt. Du börjar med  och en andra x-termin. Från koefficienten för den termen, som du kan definiera som `2b`, måste du få
och en andra x-termin. Från koefficienten för den termen, som du kan definiera som `2b`, måste du få  se för att hitta. Detta kräver en kombination av att dividera med två och sedan kvadrera resultatet.
se för att hitta. Detta kräver en kombination av att dividera med två och sedan kvadrera resultatet. 
Ta till exempel den kvadratiska funktionen  . Du kan förenkla detta genom att dividera alla termer med 2 för att få den resulterande funktionen
. Du kan förenkla detta genom att dividera alla termer med 2 för att få den resulterande funktionen  att få. Koefficienten 2 stannar utanför parentesen och kommer att vara en del av din slutliga lösning.
att få. Koefficienten 2 stannar utanför parentesen och kommer att vara en del av din slutliga lösning. Om alla termer inte är multiplar av a får du bråkkoefficienter. Till exempel: funktionen  kommer att förenklas till
kommer att förenklas till  . Arbeta ut bråken noggrant.
. Arbeta ut bråken noggrant. 
Till exempel, om de två första termerna i din kvadratiska funktion  du hittar den nödvändiga tredje termen genom att dividera 3 med 2 (eller 3/2) och sedan kvadrera det för att få 9/4. Den kvadratiska
du hittar den nödvändiga tredje termen genom att dividera 3 med 2 (eller 3/2) och sedan kvadrera det för att få 9/4. Den kvadratiska  är en perfekt fyrkant.
är en perfekt fyrkant. Ett annat exempel: anta att de två första termerna  är. Hälften av mellantermen är -2, och sedan kvadrerar du den för att få 4. Den resulterande perfekta kvadraten är
är. Hälften av mellantermen är -2, och sedan kvadrerar du den för att få 4. Den resulterande perfekta kvadraten är  .
. 
Anta att du har funktionen  . Som nämnts ovan använder du de två första termerna för att komplettera kvadraten. Genom att använda mellantermen -4x genererar du en tredje term +4. Lägg till 4 och subtrahera 4 från ekvationen, i formuläret
. Som nämnts ovan använder du de två första termerna för att komplettera kvadraten. Genom att använda mellantermen -4x genererar du en tredje term +4. Lägg till 4 och subtrahera 4 från ekvationen, i formuläret  . Parenteserna är bara placerade för att definiera den andragradsekvation du gör. Notera +4 inuti parentesen och -4 på utsidan. Förenkla siffrorna till resultatet
. Parenteserna är bara placerade för att definiera den andragradsekvation du gör. Notera +4 inuti parentesen och -4 på utsidan. Förenkla siffrorna till resultatet  .
. 
Observera att för denna funktion a=1, h=2 och k=5. Värdet av att skriva ekvationen i den här formen är att en, eftersom den är positiv, talar om för dig att parabeln pekar uppåt. Värdena (h, k) indikerar vertexen längst ner på parabeln, om du vill rita den. 
Fortsätt arbeta med förhandsgranskningsfunktionen  . Eftersom detta är i standardformat kan du bestämma vertex som x=2, y=5. Så för att undvika symmetrin arbetar du bara med höger sida av grafen och ställer in domänen om alla värden x≥2. Att infoga värdet x=2 i funktionen returnerar y=5. Du kan se att värdena på y kommer att öka när x ökar. Därför är området för denna ekvation y≥5.
. Eftersom detta är i standardformat kan du bestämma vertex som x=2, y=5. Så för att undvika symmetrin arbetar du bara med höger sida av grafen och ställer in domänen om alla värden x≥2. Att infoga värdet x=2 i funktionen returnerar y=5. Du kan se att värdena på y kommer att öka när x ökar. Därför är området för denna ekvation y≥5. 
Fortsätt arbeta med funktionen  . Infoga x i stället för f(x), och infoga y (eller f(x), om du föredrar det) i stället för x. Detta ger som en ny funktion
. Infoga x i stället för f(x), och infoga y (eller f(x), om du föredrar det) i stället för x. Detta ger som en ny funktion  .
. 
 (ursprunglig utgångspunkt)
(ursprunglig utgångspunkt) (subtrahera 5 från båda sidor)
(subtrahera 5 från båda sidor)± (kvadratrot från båda sidor; kom ihåg att kvadratroten ger både positiva och negativa möjliga svar)
(kvadratrot från båda sidor; kom ihåg att kvadratroten ger både positiva och negativa möjliga svar) ± (lägg till 2 på båda sidor)
(lägg till 2 på båda sidor) 
Se lösningen av exempelekvationen ± . Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara
. Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara  var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥5. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥2 (om du tar den positiva lösningen av kvadratroten), eller y≤2 (om du väljer den negativa lösningen av kvadratroten). Kom ihåg att du ursprungligen definierade domänen som x≥2, för att hitta den inversa funktionen. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet.
var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥5. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥2 (om du tar den positiva lösningen av kvadratroten), eller y≤2 (om du väljer den negativa lösningen av kvadratroten). Kom ihåg att du ursprungligen definierade domänen som x≥2, för att hitta den inversa funktionen. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet. Jämför domänen och intervallet för inversen med originalets domän och intervall. Kom ihåg att för den ursprungliga funktionen definierades domänen som alla värden på x≥2, och intervallet definierades som alla värden på y≥5. För denna inversa funktion byter dessa värden, och domänen är nu alla värden på x≥5, och intervallet är alla värden på y≥2. 
Som ett exempel, välj värdet x=3 som ska inkluderas i den ursprungliga ekvationen  att bearbeta. Detta ger resultatet y=6.
att bearbeta. Detta ger resultatet y=6. Sedan bearbetar man y=6 i den inversa funktionen  . Detta returnerar y=3, vilket är talet du började med. Du kan dra slutsatsen att din inversa funktion är korrekt.
. Detta returnerar y=3, vilket är talet du började med. Du kan dra slutsatsen att din inversa funktion är korrekt. 

För det här avsnittet av den här artikeln använder du exempelekvationen  .
. 

Baserat på arbetsekvationen  , ger detta resultatet
, ger detta resultatet  .
. 
För att få den vänstra sidan lika med noll i exempelekvationen måste du subtrahera x från båda sidor av ekvationen. Detta ger resultatet  .
. 
Lämna  . Alltså, x=1
. Alltså, x=1 Lämna  . Så b=2
. Så b=2 Lämna  . Så, c=(-3-x)
. Så, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-invers = -1±√(4+x)(Detta sista steget är möjligt eftersom du bytte f(x) mot variabeln x i ett tidigare skede). 




Utgår från den ursprungliga funktionen  , välj din x=-2. Detta returnerar y=-3. Ersätt nu värdet av x=-3 i den inversa funktionen,
, välj din x=-2. Detta returnerar y=-3. Ersätt nu värdet av x=-3 i den inversa funktionen,  . Detta returnerar -2, vilket verkligen är värdet du började med. Så din definition av den inversa funktionen är korrekt.
. Detta returnerar -2, vilket verkligen är värdet du började med. Så din definition av den inversa funktionen är korrekt.
Hitta inversen av en andragradsekvation
Omvända funktioner kan vara till stor hjälp för att lösa många matematiska problem. Att kunna ta en funktion och hitta dess inversa funktion är ett kraftfullt verktyg. Men med andragradsekvationer kan detta vara en ganska komplicerad process. Först måste du noggrant definiera ekvationen genom att bestämma en lämplig domän och intervall. Du kan sedan välja mellan tre metoder för att beräkna den inversa funktionen. Valet av metod är främst en fråga om personlig preferens.
Steg
Metod 1 av 3: Hitta inversen av en enkel funktion

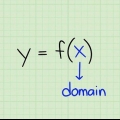
1. Hitta en funktion i form av y = a X 2 + c  . Om du har "rätt" typ av funktion att börja med, kan du hitta inversen med någon enkel algebra. Denna form är en sorts variation på
. Om du har "rätt" typ av funktion att börja med, kan du hitta inversen med någon enkel algebra. Denna form är en sorts variation på  . Om man jämför detta med en vanlig kvadratisk funktion,
. Om man jämför detta med en vanlig kvadratisk funktion,  , se att mellantermen
, se att mellantermen  saknas. Ett annat sätt att säga detta är att värdet på b är noll. Om din funktion har denna form är det ganska lätt att hitta inversen.
saknas. Ett annat sätt att säga detta är att värdet på b är noll. Om din funktion har denna form är det ganska lätt att hitta inversen.
 . Om du har "rätt" typ av funktion att börja med, kan du hitta inversen med någon enkel algebra. Denna form är en sorts variation på
. Om du har "rätt" typ av funktion att börja med, kan du hitta inversen med någon enkel algebra. Denna form är en sorts variation på  . Om man jämför detta med en vanlig kvadratisk funktion,
. Om man jämför detta med en vanlig kvadratisk funktion,  , se att mellantermen
, se att mellantermen  saknas. Ett annat sätt att säga detta är att värdet på b är noll. Om din funktion har denna form är det ganska lätt att hitta inversen.
saknas. Ett annat sätt att säga detta är att värdet på b är noll. Om din funktion har denna form är det ganska lätt att hitta inversen. - Din startfunktion behöver inte se ut exakt som
. Så länge du kan titta på det och se att funktionen bara består av
termer och konstanta tal, kommer du att kunna använda denna metod.
- Anta att du börjar med ekvationen
. En snabb undersökning av denna ekvation visar att det inte finns några termer för
att vara till första makten. Denna ekvation är en kandidat för denna metod för att hitta en invers funktion.

2. Förenkla genom att kombinera liknande termer. Den initiala ekvationen kan ha flera termer i en kombination av addition och subtraktion. Ditt första steg är att kombinera liknande termer för att förenkla ekvationen och skriva om den i standardformatet  .
.
 .
. , där y-termerna kan flyttas åt vänster genom att subtrahera ett y från båda sidor. De andra termerna kan flyttas till höger sida genom att lägga till 6 på båda sidor och
, där y-termerna kan flyttas åt vänster genom att subtrahera ett y från båda sidor. De andra termerna kan flyttas till höger sida genom att lägga till 6 på båda sidor och  att dra av från båda sidor. Den resulterande ekvationen är
att dra av från båda sidor. Den resulterande ekvationen är  .
.
3. Bestäm domänen och räckvidden för den förenklade funktionen. Kom ihåg att domänen för en funktion består av de möjliga värdena på x som kan användas för att ge en verklig lösning. Omfånget för en funktion består av värdena på y som kommer tillbaka. För att bestämma funktionens domän, leta efter värden som ger ett matematiskt omöjligt resultat. Du anger sedan domänen om alla andra värden på x. För att hitta intervallet, överväga värdena för y vid godtyckliga gränspunkter och titta på funktionens beteende.
 . Det finns ingen begränsning för de tillåtna värdena för x för denna ekvation. Du måste dock inse att detta är ekvationen för en parabel, med x=0 som centrum, och en parabel är inte en funktion eftersom det inte är en en-till-en jämförelse av x- och y-värden. För att begränsa denna ekvation och göra den till en funktion, för vilken vi kan hitta en invers, måste vi definiera domänen som x≥0.
. Det finns ingen begränsning för de tillåtna värdena för x för denna ekvation. Du måste dock inse att detta är ekvationen för en parabel, med x=0 som centrum, och en parabel är inte en funktion eftersom det inte är en en-till-en jämförelse av x- och y-värden. För att begränsa denna ekvation och göra den till en funktion, för vilken vi kan hitta en invers, måste vi definiera domänen som x≥0. , kommer alltid att vara positiv eller 0, för valfritt värde på x. Om ekvationen sedan adderar +2, kommer intervallet att vara vilket värde som helst y≥2.
, kommer alltid att vara positiv eller 0, för valfritt värde på x. Om ekvationen sedan adderar +2, kommer intervallet att vara vilket värde som helst y≥2.
4. Byt roller för x- och y-termerna. Utan att ändra ekvationen på något annat sätt måste du ersätta alla former av y med x, och alla former av x med y. Detta är steget som faktiskt "inverterar" ekvationen.
 , detta inversionssteg kommer att resultera i den nya ekvationen av
, detta inversionssteg kommer att resultera i den nya ekvationen av  .
. eller
eller  för att indikera den inversa funktionen.
för att indikera den inversa funktionen.
5. Skriv om den omvända ekvationen i termer av y. Genom att använda en kombination av algebraiska steg och se till att samma operation utförs på båda sidor av ekvationen, måste du isolera variabeln y. För jämförelsen  , denna version ser ut så här:
, denna version ser ut så här:
 , denna version ser ut så här:
, denna version ser ut så här: (ursprunglig premiss)
(ursprunglig premiss) (subtrahera 2 från båda sidor)
(subtrahera 2 från båda sidor) (diva båda sidor med 2)
(diva båda sidor med 2) (kvadratroten från båda sidor; kom ihåg att kvadratroten resulterar i både positiva och negativa möjliga svar)
(kvadratroten från båda sidor; kom ihåg att kvadratroten resulterar i både positiva och negativa möjliga svar)
6. Bestäm domänen och omfånget för den inversa funktionen. Som i början, undersök den inverterade ekvationen för att bestämma domänen och intervallet. Med två möjliga lösningar, välj den lösning som har en domän och ett intervall som är inversen av den ursprungliga domänen och intervallet.
 . Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara
. Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara  var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥2. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥0, om du tar den positiva lösningen av kvadratroten, eller y≤0, om du tar den negativa lösningen av kvadratroten. Observera att för att hitta den inversa funktionen definierade du ursprungligen domänen som x≥0. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet.
var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥2. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥0, om du tar den positiva lösningen av kvadratroten, eller y≤0, om du tar den negativa lösningen av kvadratroten. Observera att för att hitta den inversa funktionen definierade du ursprungligen domänen som x≥0. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet. , domänen definierades som alla värden på x≥0, och intervallet definierades som alla värden på y≥2. För den inversa funktionen byter nu dessa värden, och domänen är alla värden på x≥2, och intervallet är alla värden på y≥0.
, domänen definierades som alla värden på x≥0, och intervallet definierades som alla värden på y≥2. För den inversa funktionen byter nu dessa värden, och domänen är alla värden på x≥2, och intervallet är alla värden på y≥0.
7. Kontrollera om din omvända funktion fungerar. För att säkerställa att ditt arbete är korrekt och din invers är den korrekta ekvationen, välj valfritt värde för x och placera det i den ursprungliga ekvationen för att hitta y. Sätt sedan värdet på y i stället för x i din inversa ekvation och se om du får talet du började med. Om så är fallet är din inversa funktion korrekt.
 . Detta ger resultatet y=4.
. Detta ger resultatet y=4. . Detta ger verkligen resultatet y=1. Du kan dra slutsatsen att din inversa funktion är korrekt.
. Detta ger verkligen resultatet y=1. Du kan dra slutsatsen att din inversa funktion är korrekt.Metod 2 av 3: Fyll i kvadraten för att hitta den inversa funktionen

1. Ge andragradsekvationen rätt form. För att hitta inversen måste du börja med formens ekvation  . Om det behövs måste du kombinera liknande termer för att få ekvationen i detta format. Med ekvationen skriven så här kan du berätta lite mer om den.
. Om det behövs måste du kombinera liknande termer för att få ekvationen i detta format. Med ekvationen skriven så här kan du berätta lite mer om den.
 . Om det behövs måste du kombinera liknande termer för att få ekvationen i detta format. Med ekvationen skriven så här kan du berätta lite mer om den.
. Om det behövs måste du kombinera liknande termer för att få ekvationen i detta format. Med ekvationen skriven så här kan du berätta lite mer om den. - Det första du kommer att lägga märke till är värdet på koefficienten a. Om en>0, då definierar ekvationen en parabel vars ändar pekar uppåt (dalparabel). Om en<0, då definierar ekvationen en parabel vars ändar pekar nedåt (bergsparabel). Observera att a≠0. Om det inte var det skulle detta vara en linjär funktion och inte en kvadratisk.

2. Känn igen standardformatet för kvadraten. Innan du kan hitta den inversa funktionen måste du skriva om ekvationen i standardformatet. Standardformatet för en kvadratisk funktion är  . De numeriska termerna a, h och k kommer att utvärderas om du transformerar ekvationen genom att beräkna kvadraten.
. De numeriska termerna a, h och k kommer att utvärderas om du transformerar ekvationen genom att beräkna kvadraten.
 . De numeriska termerna a, h och k kommer att utvärderas om du transformerar ekvationen genom att beräkna kvadraten.
. De numeriska termerna a, h och k kommer att utvärderas om du transformerar ekvationen genom att beräkna kvadraten. , som sedan modifieras av de andra två elementen a och k. För att komma fram till denna perfekta andragradsform måste du skapa vissa villkor i din andragradsekvation.
, som sedan modifieras av de andra två elementen a och k. För att komma fram till denna perfekta andragradsform måste du skapa vissa villkor i din andragradsekvation.
3. Tänk tillbaka på formen av en perfekt kvadratisk funktion. Kom ihåg att en kvadratisk funktion som är en perfekt kvadrat uppstår från två binomialer av  , eller
, eller  . Om du gör denna multiplikation får du
. Om du gör denna multiplikation får du  . Så den första termen i andragraden är den första termen i binomialen, kvadratisk, och den sista termen i andragraden är kvadraten på den andra termen i binomialen. Mellantermen består av två gånger produkten av de två termerna, i detta fall
. Så den första termen i andragraden är den första termen i binomialen, kvadratisk, och den sista termen i andragraden är kvadraten på den andra termen i binomialen. Mellantermen består av två gånger produkten av de två termerna, i detta fall  .
.
 , eller
, eller  . Om du gör denna multiplikation får du
. Om du gör denna multiplikation får du  . Så den första termen i andragraden är den första termen i binomialen, kvadratisk, och den sista termen i andragraden är kvadraten på den andra termen i binomialen. Mellantermen består av två gånger produkten av de två termerna, i detta fall
. Så den första termen i andragraden är den första termen i binomialen, kvadratisk, och den sista termen i andragraden är kvadraten på den andra termen i binomialen. Mellantermen består av två gånger produkten av de två termerna, i detta fall  .
. och en andra x-termin. Från koefficienten för den termen, som du kan definiera som `2b`, måste du få
och en andra x-termin. Från koefficienten för den termen, som du kan definiera som `2b`, måste du få  se för att hitta. Detta kräver en kombination av att dividera med två och sedan kvadrera resultatet.
se för att hitta. Detta kräver en kombination av att dividera med två och sedan kvadrera resultatet.
4. Se till att koefficienten för X 2  1 är. Kommer du ihåg den ursprungliga formen av den kvadratiska funktionen
1 är. Kommer du ihåg den ursprungliga formen av den kvadratiska funktionen  . Om den första koefficienten är något annat än 1, måste du dividera alla termer med det värdet för att få a=1.
. Om den första koefficienten är något annat än 1, måste du dividera alla termer med det värdet för att få a=1.
 1 är. Kommer du ihåg den ursprungliga formen av den kvadratiska funktionen
1 är. Kommer du ihåg den ursprungliga formen av den kvadratiska funktionen  . Om den första koefficienten är något annat än 1, måste du dividera alla termer med det värdet för att få a=1.
. Om den första koefficienten är något annat än 1, måste du dividera alla termer med det värdet för att få a=1. . Du kan förenkla detta genom att dividera alla termer med 2 för att få den resulterande funktionen
. Du kan förenkla detta genom att dividera alla termer med 2 för att få den resulterande funktionen  att få. Koefficienten 2 stannar utanför parentesen och kommer att vara en del av din slutliga lösning.
att få. Koefficienten 2 stannar utanför parentesen och kommer att vara en del av din slutliga lösning. kommer att förenklas till
kommer att förenklas till  . Arbeta ut bråken noggrant.
. Arbeta ut bråken noggrant.
5. Hitta hälften av den mellersta koefficienten och kvadrera den. Du har redan de två första termerna i kvadratformeln. Dessa är termen  och koefficienten som representerar x-termen. Om du tar den koefficienten som värdet den har, kan du lägga till eller subtrahera talet som behövs för att göra en perfekt kvadrat. Kom ihåg från ovan att den nödvändiga tredje termen i kvadraten är denna andra koefficient dividerad med två, och sedan kvadratisk.
och koefficienten som representerar x-termen. Om du tar den koefficienten som värdet den har, kan du lägga till eller subtrahera talet som behövs för att göra en perfekt kvadrat. Kom ihåg från ovan att den nödvändiga tredje termen i kvadraten är denna andra koefficient dividerad med två, och sedan kvadratisk.
 och koefficienten som representerar x-termen. Om du tar den koefficienten som värdet den har, kan du lägga till eller subtrahera talet som behövs för att göra en perfekt kvadrat. Kom ihåg från ovan att den nödvändiga tredje termen i kvadraten är denna andra koefficient dividerad med två, och sedan kvadratisk.
och koefficienten som representerar x-termen. Om du tar den koefficienten som värdet den har, kan du lägga till eller subtrahera talet som behövs för att göra en perfekt kvadrat. Kom ihåg från ovan att den nödvändiga tredje termen i kvadraten är denna andra koefficient dividerad med två, och sedan kvadratisk. du hittar den nödvändiga tredje termen genom att dividera 3 med 2 (eller 3/2) och sedan kvadrera det för att få 9/4. Den kvadratiska
du hittar den nödvändiga tredje termen genom att dividera 3 med 2 (eller 3/2) och sedan kvadrera det för att få 9/4. Den kvadratiska  är en perfekt fyrkant.
är en perfekt fyrkant. är. Hälften av mellantermen är -2, och sedan kvadrerar du den för att få 4. Den resulterande perfekta kvadraten är
är. Hälften av mellantermen är -2, och sedan kvadrerar du den för att få 4. Den resulterande perfekta kvadraten är  .
.
6. Addera och subtrahera från den obligatoriska tredje termen samtidigt. Det här är ett knepigt koncept, men det fungerar. Att addera och subtrahera samma tal på olika ställen i din funktion ändrar inte riktigt värdet på funktionen. Men genom att göra detta får du din funktion i rätt form.
 . Som nämnts ovan använder du de två första termerna för att komplettera kvadraten. Genom att använda mellantermen -4x genererar du en tredje term +4. Lägg till 4 och subtrahera 4 från ekvationen, i formuläret
. Som nämnts ovan använder du de två första termerna för att komplettera kvadraten. Genom att använda mellantermen -4x genererar du en tredje term +4. Lägg till 4 och subtrahera 4 från ekvationen, i formuläret  . Parenteserna är bara placerade för att definiera den andragradsekvation du gör. Notera +4 inuti parentesen och -4 på utsidan. Förenkla siffrorna till resultatet
. Parenteserna är bara placerade för att definiera den andragradsekvation du gör. Notera +4 inuti parentesen och -4 på utsidan. Förenkla siffrorna till resultatet  .
.
7. Faktorisera andragradsekvationen. Polynomet inom parentes är en andragradsekvation, som du kan skriva om som  . I exemplet från föregående steg (
. I exemplet från föregående steg ( ) räknar du in kvadratfaktorn
) räknar du in kvadratfaktorn  . Kopiera resten av ekvationen så att din lösning
. Kopiera resten av ekvationen så att din lösning  blir. Detta är samma funktion som din ursprungliga andragradsekvation (
blir. Detta är samma funktion som din ursprungliga andragradsekvation ( ), omskriven som standardformuläret
), omskriven som standardformuläret  .
.
 . I exemplet från föregående steg (
. I exemplet från föregående steg ( ) räknar du in kvadratfaktorn
) räknar du in kvadratfaktorn  . Kopiera resten av ekvationen så att din lösning
. Kopiera resten av ekvationen så att din lösning  blir. Detta är samma funktion som din ursprungliga andragradsekvation (
blir. Detta är samma funktion som din ursprungliga andragradsekvation ( ), omskriven som standardformuläret
), omskriven som standardformuläret  .
.
8. Definiera funktionens domän och omfattning. Domänen är den uppsättning x-värden som kan användas som indata till funktionen. Intervallet är den uppsättning y-värden som kan bli resultatet. Kom ihåg att en parabel inte är en funktion med en definierbar invers, eftersom det inte finns något en-till-ett förhållande mellan x-värden och y-värden, på grund av parabelns symmetri. För att lösa detta problem måste du definiera domänen som alla värden på x som är större än x=h, parabelns vertex.
 . Eftersom detta är i standardformat kan du bestämma vertex som x=2, y=5. Så för att undvika symmetrin arbetar du bara med höger sida av grafen och ställer in domänen om alla värden x≥2. Att infoga värdet x=2 i funktionen returnerar y=5. Du kan se att värdena på y kommer att öka när x ökar. Därför är området för denna ekvation y≥5.
. Eftersom detta är i standardformat kan du bestämma vertex som x=2, y=5. Så för att undvika symmetrin arbetar du bara med höger sida av grafen och ställer in domänen om alla värden x≥2. Att infoga värdet x=2 i funktionen returnerar y=5. Du kan se att värdena på y kommer att öka när x ökar. Därför är området för denna ekvation y≥5.
9. Byt x- och y-värden. Detta är steget där du börjar med att hitta ekvationens inversa form. Lämna ekvationen i sin helhet förutom att byta dessa variabler.
 . Infoga x i stället för f(x), och infoga y (eller f(x), om du föredrar det) i stället för x. Detta ger som en ny funktion
. Infoga x i stället för f(x), och infoga y (eller f(x), om du föredrar det) i stället för x. Detta ger som en ny funktion  .
.
10. Skriv om den omvända ekvationen i termer av y. Använd en kombination av algebraiska steg, se till att du utför samma operation jämnt på båda sidor av ekvationen, isolera variabeln y. För arbetsjämförelsen  denna version ser ut så här:
denna version ser ut så här:
 denna version ser ut så här:
denna version ser ut så här: (ursprunglig utgångspunkt)
(ursprunglig utgångspunkt) (subtrahera 5 från båda sidor)
(subtrahera 5 från båda sidor) (kvadratrot från båda sidor; kom ihåg att kvadratroten ger både positiva och negativa möjliga svar)
(kvadratrot från båda sidor; kom ihåg att kvadratroten ger både positiva och negativa möjliga svar) (lägg till 2 på båda sidor)
(lägg till 2 på båda sidor)
11. Bestäm domänen och omfånget för den inversa funktionen. Som i början, undersök den omvända ekvationen för att bestämma domänen och intervallet. Med två möjliga lösningar, välj den lösning som har en domän och ett intervall som är inversen av den ursprungliga domänen och intervallet.
 . Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara
. Eftersom kvadratrotfunktionen inte är definierad för negativa värden måste termen . vara  var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥5. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥2 (om du tar den positiva lösningen av kvadratroten), eller y≤2 (om du väljer den negativa lösningen av kvadratroten). Kom ihåg att du ursprungligen definierade domänen som x≥2, för att hitta den inversa funktionen. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet.
var alltid positiv. Därför måste de tillåtna värdena för x (domänen) vara x≥5. Med det som domän är de resulterande värdena för y (intervallet) antingen alla värden y≥2 (om du tar den positiva lösningen av kvadratroten), eller y≤2 (om du väljer den negativa lösningen av kvadratroten). Kom ihåg att du ursprungligen definierade domänen som x≥2, för att hitta den inversa funktionen. Därför är den korrekta lösningen för den inversa funktionen det positiva alternativet.
12. Kontrollera om din omvända funktion fungerar. För att säkerställa att ditt arbete är korrekt och din invers är den korrekta ekvationen, välj valfritt värde för x och placera det i den ursprungliga ekvationen för att hitta y. Sätt sedan värdet på y i stället för x i din inversa ekvation och se om du får talet du började med. Om ja, är din omvända funktion korrekt.
 att bearbeta. Detta ger resultatet y=6.
att bearbeta. Detta ger resultatet y=6. . Detta returnerar y=3, vilket är talet du började med. Du kan dra slutsatsen att din inversa funktion är korrekt.
. Detta returnerar y=3, vilket är talet du började med. Du kan dra slutsatsen att din inversa funktion är korrekt.Metod 3 av 3: Använd kvadratformeln

1. Använd den kvadratiska formeln för att lösa x. Kom ihåg att när du löser andragradsekvationer finns det en metod för att faktorisera dem (om möjligt). Om factoring inte fungerade kan du använda kvadratformeln, som skulle ge de verkliga lösningarna till vilken andragradsekvation som helst. Du kan också använda kvadratformeln som en metod för att hitta inversa funktioner.
- Kvadratisk formel är x=[-b±√(b^2-4ac)]/2a.
- Observera att kvadratformeln ger två möjliga lösningar, en positiv och en negativ. Du kommer att göra detta val baserat på att bestämma funktionens domän och omfattning.

2. Börja med en andragradsekvation för att hitta inversen. Din andragradsekvation bör börja i formatet  . Ta de algebraiska stegen som behövs för att få din ekvation i den formen.
. Ta de algebraiska stegen som behövs för att få din ekvation i den formen.
 . Ta de algebraiska stegen som behövs för att få din ekvation i den formen.
. Ta de algebraiska stegen som behövs för att få din ekvation i den formen. .
.
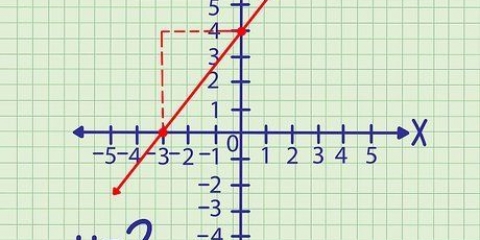
3. Rita ekvationen för att bestämma domänen och intervallet. Plotta funktionen, antingen med hjälp av en grafräknare eller rita flera punkter tills du kan rita parabeln. Du kommer att se att denna ekvation definierar en parabel med den högsta punkten vid (-1,-4). Så för att definiera detta som en funktion som kommer att ha en invers, definierar du domänen som alla värden på x≤-1. Området är då alla värden y≥-4.

4. Byt ut variablerna x och y. För att hitta inversen byter du variablerna x och y. Lämna ekvationen oförändrad, förutom att byta ut variablerna. I detta skede, ersätt x med f(x).
 , ger detta resultatet
, ger detta resultatet  .
.
5. Ställ in den vänstra sidan av ekvationen lika med noll. Kom ihåg att för att använda andragradsformeln måste du sätta ekvationen lika med noll, använd sedan koefficienterna i formeln. På samma sätt börjar denna metod för att hitta en invers funktion med att sätta ekvationen lika med noll.
 .
.
6. Omdefiniera variablerna så att de passar kvadratformeln. Det här steget är lite knepigt. Vet att kvadratformeln löser x i ekvationen  . Så för ekvationen du har nu,
. Så för ekvationen du har nu,  , för att följa den klassificeringen måste du omdefiniera termerna enligt följande:
, för att följa den klassificeringen måste du omdefiniera termerna enligt följande:
 . Så för ekvationen du har nu,
. Så för ekvationen du har nu,  , för att följa den klassificeringen måste du omdefiniera termerna enligt följande:
, för att följa den klassificeringen måste du omdefiniera termerna enligt följande: . Alltså, x=1
. Alltså, x=1 . Så b=2
. Så b=2 . Så, c=(-3-x)
. Så, c=(-3-x)
7. Lös kvadratformeln med dessa omdefinierade värden. Normalt skulle du bearbeta värdena för a, b och c i kvadratformeln för att lösa x. Kom dock ihåg att du tidigare bytte x och y för att hitta den inversa funktionen. Så när du använder kvadratformeln för att lösa x, löser du faktiskt y, eller f-inversen. Stegen för att lösa kvadratformeln fungerar enligt följande:

8. Skriv ner de två möjliga lösningarna. Observera att kvadratformeln ger två möjliga utfall, med hjälp av symbolen ±. Skriv ut de två separata lösningarna för att göra det lättare att bestämma domänen och intervallet och ge den korrekta slutliga lösningen. Dessa två lösningar är:



9. Bestäm domänen och omfånget för den inversa funktionen. Observera att för att definiera kvadratroten måste domänen vara x≥-4. Kom ihåg att domänen för den ursprungliga funktionen var x≤-1 och intervallet var y≥-4. För att välja den inversa funktionen som motsvarar, behöver du den andra lösningen,  välj som korrekt invers funktion.
välj som korrekt invers funktion.
 välj som korrekt invers funktion.
välj som korrekt invers funktion.
10. Kontrollera om din inversa funktion är korrekt. För att se till att ditt arbete är korrekt och din invers är den korrekta ekvationen, välj valfritt värde för x och sätt det i den ursprungliga ekvationen för att hitta y. Sätt sedan värdet på y i stället för x i din inversa ekvation och se om du får talet du började med. Om ja, är din omvända funktion korrekt.
 , välj din x=-2. Detta returnerar y=-3. Ersätt nu värdet av x=-3 i den inversa funktionen,
, välj din x=-2. Detta returnerar y=-3. Ersätt nu värdet av x=-3 i den inversa funktionen,  . Detta returnerar -2, vilket verkligen är värdet du började med. Så din definition av den inversa funktionen är korrekt.
. Detta returnerar -2, vilket verkligen är värdet du började med. Så din definition av den inversa funktionen är korrekt. "Hitta inversen av en andragradsekvation"
Оцените, пожалуйста статью