I allmänna ordalag, A+B = Låt oss lägga till de två vektorerna A och B. A = <5, 9, -10> och B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, eller <22, 6, -12>. 
I allmänna ordalag, A-B = Låt oss subtrahera de två vektorerna A och B. A = <18, 5, 3> och B = <-10, 9, -10>. A - B = <18--10, 5-9, 3--10>, eller <28, -4, 13>. 

Observera att ordningen i vilken du ritar vektorerna inte är viktig, så länge vi antar att du alltid använder samma utgångspunkt. Vektor A + Vektor B = Vektor B + Vektor A 


Eftersom du har ritat alla vektorer i skala och mätt vinklarna exakt, kan du hitta storleken på den resulterande vektorn genom att mäta längden. Du kan också mäta vinkeln som denna resultant gör med en specifik vektor eller med den horisontella/vertikala etc. för att hitta riktningen. Eftersom du inte har ritat alla vektorer i skala, måste du förmodligen beräkna storleken på resultanten med hjälp av trigonometri. Använd sinus- eller cosinusregeln för detta. Eftersom du lägger till fler än två vektorer är det bra att lägga till två av dem först, sedan lägga till deras resultant till den tredje vektorn, och så vidare. Se nästa avsnitt för mer information. 
Till exempel, om vektorerna vi lagt till representerar en hastighetsvektor i ms, då kan vi representera den resulterande vektorn som "en hastighetsvektor av X ms kl y i förhållande till det horisontella". 

Till exempel tar vi vektorn från föregående steg, <-2.12 och 2.12>, och lägg till den i vektorn <5,78 och -9>. I det här fallet är vår resulterande vektor <-2,12+5.78 och 2,12-9>, eller <3,66 och -6,88>. 
För att hitta storleken på vektorn vars komponenter vi bestämde i föregående steg, <3,66 och -6,88>, vi använder Pythagoras sats. Lös enligt följande: c=(3,66)+(-6,88) c=13,40+47,33 c=√60,73 = 7,79 
För att bestämma riktningen för vår exempelvektor använder vi θ=tan(b/a). θ=tan(-6.88/3.66) θ=tan(-1.88) 6=-61.99 
Till exempel, om exempelvektorn representerar en kraft (i Newton), kan vi skriva detta som "en kraft av 7,79 Icke -61,99 från det horisontella".
Beräknar med vektorer
Vektorer är storheter som består av en magnitud och en riktning (till exempel: hastighetsvektor eller vektoriell hastighet, acceleration och förskjutning), till skillnad från skalärer, som bara har magnitud (som hastighet, avstånd och energi). Medan skalärer kan läggas ihop genom deras storlekar (t.ex. 5 kJ + 6 kJ = 11 kJ), är vektorer lite mer komplicerade att beräkna med. Se steg 1 nedan för att lära dig mer om sätt att göra detta.
Steg
Metod 1 av 3: Addera och subtrahera vektorer

1. Uttryck dimensionerna för en vektor med hjälp av vektornotation. Eftersom vektorer har en storlek och en riktning är det vanligtvis lätt att dela upp dem i deras x-, y- och/eller z-dimensioner. Dessa dimensioner uttrycks vanligtvis i en notation som motsvarar att beskriva en punkt i ett koordinatsystem (t.ex. Observera att vektorer kan vara 1-, 2- eller 3-dimensionella. Så, vektorer kan ha en x-komponent, en x- och y-komponent, eller en x, y etc-komponent. Vårt exempel nedan handlar om 3-dimensionella vektorer, men processen liknar den för planet eller en linje. Låt oss anta att vi har två 3-dimensionella vektorer, vektor A och vektor B. Vi kan skriva dessa vektorer i vektornotation som A =

2. Lägg till komponenterna för att lägga till två vektorer. Om komponenterna i två vektorer är kända, är det möjligt att bestämma vektorerna genom att addera deras motsvarande komponenter. Med andra ord, lägg till x-komponenten för den första vektorn till x-komponenten för den andra och gör samma sak för y och z. Svaren du får genom att lägga till x-, y- och z-komponenterna i de ursprungliga vektorerna är x-, y- och z-komponenterna i den nya vektorn.

3. För att subtrahera två vektorer subtraherar du deras komponenter. Alltså samma som med addition, fast omvänt.Om komponenterna i två vektorer är kända, så är subtrahering av en vektor från den andra inte mer än att subtrahera komponenterna.
Metod 2 av 3: Addition och subtraktion med den bakre metoden

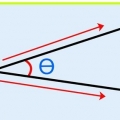
1. Ange vektorer med en pil. Eftersom vektorer har en storlek och en riktning kan du ange dem med en pil. De har med andra ord en "utgångspunkt" och a "slutpunkt", pekar i vektorns riktning, med storleken på vektorn indikerad av pilen.
- När du ritar en vektor i skala måste du mäta vinklarna noggrant. Fel vinklar kommer att resultera i ett felaktigt svar med denna metod.

2. Rita pilarna i bakre ordning. Pilens huvud placeras mot svansen på nästa pil. Eftersom du bara lägger till två vektorer, är detta allt du behöver göra för att hitta den resulterande vektorn.

3. För att subtrahera gör vektorn "negativ". Att subtrahera vektorer med denna visuella metod är relativt enkelt. Vänd riktningen på vektorn, men behåll storleken densamma och lägg till den med huvud-till-svans-metoden som vanligt. Med andra ord, för att subtrahera en vektor, roterar du vektorn 180 och adderar.

4. Om du vill lägga till eller subtrahera mer än två vektorer, länka sedan alla dessa vektorer efter varandra med den bakre metoden. Ordningen spelar ingen roll. Du kan använda detta för valfritt antal vektorer.
5. Rita en ny vektor från svansen på den första vektorn till huvudet på den sista. Oavsett om du arbetar med 2 eller 100 vektorer, är vektorn som sträcker sig från startpunkten (svansen på din första vektor) till slutpunkten för de tillagda vektorerna (huvudet på din sista vektor) resultatet vektor, eller summan av alla vektorer. Observera att denna vektor är lika med vektorn som erhålls genom att addera x-, y- och/eller z-komponenterna för alla vektorer.


6. Visa den resulterande vektorn efter storlek och riktning. Vektorer bestäms av deras längd och riktning. Som nämnts ovan, förutsatt att du har ritat vektorerna korrekt, är storleken på vektorn lika med dess längd och riktning, och dess vinkel är relativt vertikal, horisontell, etc. Använd enheterna för de vektorer du lagt till för att välja enheter för storleken på den resulterande vektorn.
Metod 3 av 3: Addera och subtrahera vektorer genom att bestämma komponenterna

1. Använd trigonometri för att hitta vektorns komponenter. Du behöver storleken och riktningen relativt horisontellt eller vertikalt, och du behöver ha viss praktisk kunskap om trigonometri. Antag att vi har en 2D-vektor. Först gör du vektorerna till hypotenusan av en rätvinklig triangel, med de andra två sidorna parallella med x- och y-axlarna. Du kan tänka på dessa två sidor som huvud-till-svans-vektorer som, när de läggs ihop, ger den ursprungliga vektorn.
- Längden på de två sidorna är lika med storleken på x- och y-komponenterna i din vektor och kan beräknas med hjälp av trigonometri. Om x är storleken på vektorn, då sidan som gränsar till vektorns vinkel (i förhållande till horisontal, vertikal, etc.) lika med xcos(θ), medan motsatsen är lika med xsin(θ).
- Det är också viktigt att överväga orienteringen av dina komponenter. Om komponenten pekar i negativ riktning för en av axlarna får den ett minustecken. Till exempel, om en komponent pekar till vänster eller till botten i planet, får den ett minustecken.
- Låt oss till exempel säga att vi har en vektor med magnitud 3 och en riktning 135 i förhållande till horisontalplanet. Med denna information kan vi fastställa att x-komponenten är lika med 3cos(135) = -2.12 och y-komponenten är 3sin(135) = 2.12

2. Lägg ihop motsvarande komponenter av två eller flera vektorer. När du har hittat komponenterna i alla vektorerna lägger du helt enkelt ihop magnituderna för att hitta komponenterna i din resulterande vektor. Lägg först ihop storlekarna på de horisontella komponenterna (parallellt med x-axeln). Lägg sedan till storlekarna på de vertikala komponenterna (parallellt med y-axeln). Om en komponent har ett minustecken (-) framför sig, subtraheras dess storlek. Svaren du får är komponenterna i din resulterande vektor.

3. Beräkna storleken på den resulterande vektorn med hjälp av Pythagoras sats. Med detta uttalande, c=a+b, kan du hitta längden på sidorna i räta trianglar?. Eftersom triangeln som bildas av den resulterande vektorn och dess komponenter är en rätvinklig triangel, kan vi använda denna sats för att hitta vektorns längd och därmed dess storlek. Av c som storleken på den resulterande vektorn du försöker hitta, säg a in som storleken på x-komponenten och b som storleken på y-komponenten. Lös med algebra.

4. Beräkna riktningen för resultanten med tangenten. Slutligen bestämmer vi riktningen för den resulterande vektorn. Använd formeln θ=tan(b/a), där θ är vinkeln som resultanten gör med x-axeln från horisontalplanet, där b är storleken på y-komponenten och a är storleken på x-komponenten.

5. Visa den resulterande vektorn efter storlek och riktning. Som indikerat ovan definieras vektorer av deras storlek och riktning. Se till att du använder rätt enheter för storleken på vektorn.
Tips
- Vektorer ska inte förväxlas med storlekar.
- Du kan hitta storleken på en vektor i rymden med formeln a=b+c+d att använda, var a är storleken på vektorn och före Kristus och d komponenterna i varje riktning.
- Vektorer representerade som xi + yj + zk kan adderas eller subtraheras genom att helt enkelt addera eller subtrahera koefficienterna för de tre vektorerna. Svaret har då också formen i, j, k.
- Kolumnvektorer kan adderas och subtraheras genom att lägga till eller subtrahera värdena i varje rad.
"Beräknar med vektorer"
Оцените, пожалуйста статью