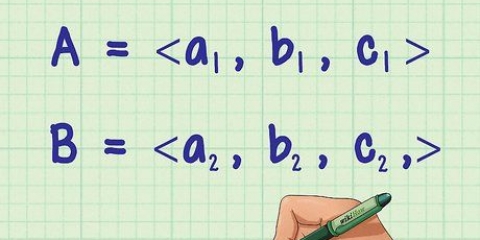Proportionsberäkning: 7 steg (med bilder)

Steg
- Del 1 av 2: Att skriva ett förhållande
- Del 2 av 2: Använda kvoter i matematiska problem
Exempel övningar
Tips
Förnödenheter

Proportioner eller förhållanden är matematiska uttryck som jämför två eller flera tal. Proportioner kan jämföra fasta mängder och antal eller kan användas för att jämföra delar av helheten. Proportioner kan beräknas och noteras på olika sätt, men principerna är desamma för alla nyckeltal. Se steg 1 nedan för att komma igång med proportioner.

Steg

Del 1 av 2: Att skriva ett förhållande

1. Förstå hur proportioner används. Relationer finns överallt, i den vetenskapliga världen eller hemma. De enklaste förhållandena jämför bara två värden, men fler är naturligtvis också möjliga.

Ett exempel: i en klass med 20 elever, varav 5 flickor och 15 pojkar, kan vi uttrycka antalet flickor och pojkar som ett förhållande.

2. Skriv ett förhållande med ett kolon. Ett vanligt sätt att ange ett förhållande är med ett kolon mellan siffrorna. Om du jämför två siffror skriver du ner det till exempel som 7 : 13 och om det finns 3 eller fler siffror så t.ex. 10 : 2 : 23.

I vårt klassrum kan vi alltså skriva förhållandet mellan flickor och pojkar enligt följande:5 flickor: 15 pojkar. Du kan valfritt utelämna beteckningen, så länge du kommer ihåg vad förhållandet står för.

3. Ett förhållande är detsamma som en bråkdel och kan därför förenklas. Du gör detta genom att dividera alla termer av förhållandet med de gemensamma divisorerna, tills det inte finns fler gemensamma divisorer kvar. Men när du gör detta är det viktigt att inte glömma vilka de ursprungliga siffrorna för förhållandet var. Se nedan.

I klassrumsexemplet var det 5 flickor och 15 pojkar. Båda sidorna av förhållandet är delbara med 5. Detta gör att du kan förenkla förhållandet till1 flicka: 3 pojkar.

Men vi bör inte tappa de ursprungliga siffrorna ur sikte. Det är inte 4 utan 20 elever totalt i klassen. Det förenklade förhållandet jämför endast förhållandet mellan antalet pojkar och flickor. Det finns 3 pojkar till 1 flicka i förhållandet eller bråkdelen, inte 3 pojkar och 1 flicka i klassen.

Vissa proportioner kan inte förenklas. Till exempel kan 3 : 56 inte förenklas eftersom de 2 talen inte har lika faktorer - 3 är primtal och 56 är inte delbart med 3.

4. Det finns också alternativa metoder för att skriva proportioner. Medan kolon kanske är det enklaste för skrivkvoter, finns det andra sätt som inte påverkar förhållandet. Se nedan:

Proportioner kan också visas som "3 står till 6" eller "11 mot 4 på 20".

Du kan också skriva proportioner som bråk. Ofta leder användningen av båda termerna till viss förvirring, men bråk är proportioner och vice versa. Så du kan också skriva ett förhållande med en divisionslinje. Till exempel förhållandet 3/5 och fraktionen 3/5 inte skiljer sig från varandra. Som i exemplet med klassen: det var 3 pojkar till varje flicka, ett förhållande på 1 : 3, men som en bråkdel uttrycker samma sak, nämligen 1/3 av det totala antalet elever är en flicka.

Del 2 av 2: Använda kvoter i matematiska problem

1. Använd multiplikation eller division för att ändra förhållandet utan att ändra förhållandet. Att multiplicera eller dividera båda termerna i ett förhållande med ett givet tal ger samma förhållande, men med större eller mindre tal.

Anta till exempel att du är lärare och att du blir ombedd att öka storleken på klassen 5 gånger, men med samma förhållande mellan pojkar och flickor. Om det är 8 tjejer och 11 killar i klassen nu, hur många är det i den nya klassen?Läs vidare för lösningen:

8 flickor och 11 pojkar, alltså ett förhållande på 8:11. Detta förhållande indikerar därför att det, oavsett storleken på klassen, finns 8 flickor till 11 pojkar.
(8 : 11) × 5
(8×5: 11×5)
(40:55). Den nya klassen består av 40 tjejer och 55 killar - 95 elever totalt!

2. Använd korsmultiplikation för att hitta den okända variabeln när du arbetar med två ekvivalenta förhållanden. Ett annat välkänt problem är att där du blir ombedd att beräkna det okända av ett förhållande. Korsmultiplikation gör det mycket enkelt att räkna ut detta. Skriv varje förhållande som en bråkdel, gör dem lika och multiplicera korsvis för att lösa.

Som ett exempel, låt oss säga att vi har en grupp elever på 2 pojkar och 5 flickor. Om vi vill behålla förhållandet intakt, hur många pojkar finns det i en grupp på 20 tjejer?För att lösa detta gör vi två förhållanden, ett med den okända variabeln: 2 pojkar : 5 flickor = x pojkar : 20 flickor. I bråkform ser det ut så här: 2/5 = x/20. Använd korsmultiplikation för att lösa detta. Se nedan:

2/5 = x/20

5 × x = 2 × 20

5x = 40

x = 40/5 = 8. Så det är 20 tjejer och 8 killar.

3. Använd kvoter för att hitta okända storheter, där en annan ges. Om du har att göra med en variabel som bestämmer sambandet mellan flera storheter, varav 1 eller fler är okända, kan du hitta värdet på varje okänt med endast en känd storhet. Dessa typer av påståenden innebär ofta att man beräknar mängden ingredienser i ett recept. För att hitta de okända kvantiteterna, dividera den kända termen av förhållandet med den givna kvantiteten; dela efteråt varje term i förhållandet av det svar du får. Ett exempel kommer att göra det hela lite tydligare:

Anta att vår klass bakar kakor som en uppgift. Om degreceptet består av mjöl, vatten och smör i förhållandet 20 : 8 : 4, och varje elev får 5 koppar mjöl; hur mycket vatten och smör behöver varje elev? För att lösa detta, dividera först termen för förhållandet som motsvarar det kända förhållandet (20) med den kända kvantiteten (5 koppar). Dela sedan varje term i förhållandet med svaret du får för att hitta det exakta beloppet för varje. Se nedan:

20/5 = 4

20/4 : 8/4 : 4/4

5 : 2 : 1. Så, 5 koppar mjöl, 2 koppar vatten och 1 kopp smör.

Exempel övningar

Kex är gjorda av smör och socker i förhållandet 5:3. Om 7 delar smör används, hur mycket socker behövs?

För att göra detta, använd förhållandet i form av en bråkdel. I det här fallet gör vi det till en decimal – cirka 1,67.
Formeln är nu redo att användas. Vi vill hitta mängden socker, så låt oss låta det vara vad det är och beräkna fraktionen smör/1,67, så 7/1,67 = 4,192

Den del som handlar om proportioner är proportionell division. När en total kvantitet delas upp i delar skapas ett förhållande. Till exempel: Annemiek, Anna och Anton arbetar alla i sin mammas butik. Annemiek arbetade en timme, Anna 3 och Anton 6 timmar (alltså ett förhållande 1:3:6). Mamma ger dem en total summa och ber dem dela upp detta själva i rätt proportion. Det totala beloppet var €100. Det gör du genom att lägga ihop delarna av förhållandet, så att du vet hur mycket varje del är värd. 1:3:6 blir då 1+3+6=10 så $100/10=$10 så vi vet nu att varje del av förhållandet är värt $10... och det är därför alla får en lön på €10 per timme. Nu kan vi använda detta för att beräkna vad var och en tjänade. Annemiek får €10, Anna får €30 och Anton får €60. Kontrollera detta genom att lägga ihop alla löner, som borde komma ut till €100. 10+30+60= 100. Korrekt!

Tips

Förenkla förhållanden genom att använda ab/c-knappen på din miniräknare (detta är för att skriva blandade bråk och förenkla). Om du till exempel har 8:12 testar du "8 ab/c 12" = in och du får 2/3, och därmed förhållandet 2:3.