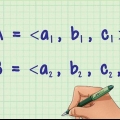Hitta vinkeln mellan två vektorer

Steg
Tips

Matematiker och fysiker måste ofta hitta vinkeln mellan två givna vektorer. Även om det är lätt att hitta vinkeln mellan två vektorer i samma plan genom att rita grafer, kan det vara lite knepigare i rymden eller i tre dimensioner. Den här artikeln förklarar metoden att använda för att hitta vinkeln mellan två vektorer i planet eller i rymden.

Steg

Metod 1 av 4: Bestäm vektorerna

1. Bestäm vektorerna du behöver för att hitta vinkeln. Ta de två vektorerna TILL och O Q som skär i punkt O, och beräkna vinkeln MOQ. Du måste använda vektorerna TILL och O Q använd, gör inte MO eller QO. I händelse av att MO är känd, multiplicera det med -1 för att få TILL att få.

Metod 2 av 4: Hitta den skalära produkten

Hitta skalärprodukten (eller punktprodukten) av de två vektorerna. Om du inte vet hur man beräknar skalärprodukten av två vektorer, läs vidare:

1. Bestäm komponenterna i vektorn i varje riktning. När vektorerna är listade i en tabell representerar den första raden vanligtvis x-axeln, den andra raden representerar y-axeln och den tredje representerar z-axeln. Om vektorn skrivs på formen xi + yj + zk, ställ sedan in koefficienterna för jag, yo, och k storleken på komponenterna längs x-, y- och z-axlarna (jag, yo, och k är vektorerna längs x-, y- och z-axlarna).

2. Multiplicera komponenterna i båda vektorerna längs x-axeln. Multiplicera sedan komponenterna för båda vektorerna längs y-axeln och gör samma sak för komponenterna längs z-axeln.

3. Lägg ihop de tre produkterna. Detta är den skalära produkten av båda vektorerna. Den skalära produkten, eller "intern produkt", av två vektorer är ett mycket användbart tal inom geometri och fysik. För närvarande använder vi endast denna produkt som ett verktyg för att beräkna vinkeln mellan två vektorer. I en tvådimensionell vektor är komponenten längs z-axeln noll, så den skalära produkten kan hittas genom att endast beakta komponenterna längs x- och y-axeln.

Metod 3 av 4: Beräkna storleken

1. Beräkna storleken på de två vektorerna. Beräkna storleken på de två vektorerna med hjälp av formeln a=b+c+d, varigenom a är storleken på vektorn, och före Kristus, och d storleken på komponenterna i de tre olika riktningarna. I det platta planet d vara lika med noll.

Metod 4 av 4: = Hitta vinkeln

1. Använd värdena som beräknats ovan i denna formel: cosθ = a.b / |a||b|

2. Härled den omvända cosinus från detta.

3. Färdiga.

Tips

Du kan använda den här metoden för att beräkna vinkeln i 3D- eller x-y-z-grafer genom att betrakta sidorna som vektorer och behandla vektorn som fria vektorer.