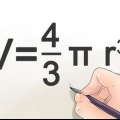Har du en sfär med en omkrets på 20 m hittar du radien med 20/2π = 3,183 m. Samma formel kan användas för att konvertera mellan radien och omkretsen av en cirkel. 
Om du har en sfär med en volym på 100 cm får du radien enligt följande: ((V/π)(3/4)) = r ((100/π)(3/4)) = r ((31.83)(3/4)) = r (23.87) = r 2,88 = r 
Om du har en sfär med en area på 1200 cm, beräknar du radien enligt följande: √(A/(4π)) = r √(1200/(4π)) = r √(300/(π)) = r √(95,49) = r 9,77 cm = r 

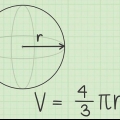
D = 2r. Precis som cirklar är diametern på en sfär två gånger dess radie. C = πD eller 2πr. Precis som cirklar är omkretsen av en sfär lika med π gånger diametern. Eftersom diametern är två gånger radien kan vi också säga att omkretsen är lika med två gånger radien gånger π. V = (4/3)πr. Volymen av en sfär är dess radie till kuben (r x r x r), gånger π, gånger 4/3. A = 4πr. Arean av en sfär är dess radie till andra potensen (r x r), gånger π, gånger 4. Eftersom en cirkels omkrets är lika med πr, kan man också säga att arean av en sfär är lika med fyra gånger arean av en cirkel, som bildas av dess omkrets. 

I samband med vår exempeluppgift konstaterar vi att poängen (3, 3, 0) på sfärens yta, ges. Genom att beräkna avståndet mellan denna punkt och mitten kan vi hitta radien. 
I vårt exempel ersätter vi (4, -1, 12) för (x1,y1,z1) och (3, 3, 0) för (x2,y2,z2), där vi löser detta enligt följande: d = √((x2 - X1) + (y2 - y1) + (z2 - z1)) d = √((3 - 4) + (3 - -1) + (0 - 12)) d = √((-1) + (4) + (-12)) d = √(1 + 16 + 144) d = √(161) d = 12,69. Detta är radien för vår sfär. 
Genom att kvadrera båda sidor av denna ekvation får vi: r = (x2 - X1) + (y2 - y1) + (z2 - z1). Obs: Detta motsvarar i huvudsak standardekvationen för en sfär (r = x + y + z), förutsatt att dess centrum är lika med (0,0,0).
Beräknar radien för en sfär
Radien för en sfär (förkortad som variabeln r eller R) är avståndet från sfärens exakta centrum till en punkt på sfärens yta. Precis som cirklar, en sfärs radie är ofta en viktig första data för beräkning av en sfärs diameter, omkrets, area och volym. Du kan dock även arbeta baklänges från diameter, omkrets osv. för att hitta sfärens radie. Använd formeln som är lämplig för de data du har.
Steg
Metod 1 av 3: Använd radieformler

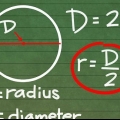
1. Bestäm radien om du känner till diametern. Radien är en halv diameter, så du använder formeln r = D/2. Detta är identiskt med metoden för att beräkna radien för en cirkel givet diametern.
- Om du har en sfär med en diameter på 16 cm, beräknar du radien med 16/2 = 8 cm. Om diametern är 42, då radien 21.

2. Bestäm radien om du känner till omkretsen. Använd formeln C/2π. Eftersom omkretsen är lika med πD, som i sin tur är lika med 2πr, räknar man ut radien genom att dividera omkretsen med 2π.

3. Beräkna radien om du känner till sfärens volym. Använd formeln ((V/π)(3/4)). Volymen av en sfär härleds från ekvationen V = (4/3)πr.Genom att lösa ekvationen för r får man ((V/π)(3/4)) = r, så det blir tydligt att en sfärs radie är lika med volymen dividerat med π, gånger 3/4 , upphöjd till 1/3-potensen (eller kubroten).

4. Bestäm ytans radie. Använd formeln r = √(A/(4π)). Arean av en sfär beräknas med hjälp av ekvationen A = 4πr. Att lösa ekvationen för r ger √(A/(4π)) = r, vilket betyder att en sfärs radie är lika med kvadratroten av dess area dividerat med 4π. Du kan också driva (A/(4π)) till 1/2 för samma resultat.
Metod 2 av 3: Definiera nyckeltermer

1. Känna till de grundläggande dimensionerna av en sfär. Radien (r) är avståndet från sfärens exakta centrum till valfri punkt på sfärens yta. I allmänhet kan du hitta radien för en sfär om du känner till dess diameter, omkrets, volym eller area.
- Diameter (D): längden på linjen genom mitten av en sfär & ndash; dubbla radien. Diametern är längden på en linje genom sfärens centrum: från en punkt på sfärens utsida till en motsvarande punkt mittemot den. Med andra ord största möjliga avstånd mellan två punkter på sfären.
- Omkrets (C): det endimensionella avståndet runt sfären på dess bredaste punkt. Med andra ord, omkretsen av det cirkulära tvärsnittet av en sfär vars plan passerar genom sfärens centrum.
- Volym (V): det tredimensionella rummet inom sfären. Det är "utrymme som upptas av sfären".
- Område (A): det tvådimensionella utrymmet på sfärens yttre yta. Mängden platt utrymme som täcker utsidan av sfären.
- pi (π): en konstant som uttrycker förhållandet mellan cirkelns omkrets och cirkelns diameter. De första 10 siffrorna i Pi är alltid 3,141592653, även om detta vanligtvis avrundas till 3.14.

2. Använd olika avläsningar för att bestämma radien. Du kan använda diametern, omkretsen, volymen och arean för att beräkna radien för en sfär. Om du vet längden på radien kan du beräkna vilket som helst av dessa tal. Så för att hitta radien kan du vända om formlerna för att beräkna dessa delar. Lär dig formlerna som involverar radie för att beräkna diameter, omkrets, area och volym.
Metod 3 av 3: Hitta radien som avståndet mellan två punkter

1. Bestäm koordinaterna (x, y, z) för sfärens centrum. Ett sätt att tänka på en sfärs radie är som avståndet mellan sfärens centrum och någon punkt på dess yta. Eftersom detta är sant kan du bestämma sfärens radie med hjälp av koordinaterna för mitten och en punkt på sfärens yta, genom att beräkna avståndet mellan de två punkterna med en variant av standardavståndsformeln. För att börja, hitta koordinaterna för mitten av sfären. Observera att en sfär är tredimensionell, detta kommer att vara en (x, y, z) punkt istället för en (x, y) punkt.
- Detta är lättare att förstå med ett exempel. Antag att en sfär ges med som centrum(-1, 4, 12). I de kommande stegen kommer vi att använda denna punkt när vi bestämmer radien.

2. Bestäm koordinaterna för en punkt på sfärens yta. Sedan måste du bestämma (x, y, z) koordinaterna för en punkt på sfärens yta. Det här är möjligt varje punkt på sfärens yta. Eftersom per definition alla punkter på en sfärs yta är lika långt från mitten, kan du använda vilken punkt som helst för att bestämma radien.

3. Bestäm radien med formeln d = √((x2 - X1) + (y2 - y1) + (z2 - z1)). Nu när du känner till sfärens centrum och en punkt på sfärens yta kan du ta reda på radien genom att beräkna avståndet mellan dem. Använd den tredimensionella avståndsformeln d = √((x2 - X1) + (y2 - y1) + (z2 - z1)), där d är avståndet, (x1,y1,z1) representerar koordinaterna för mittpunkten, och (x2,y2,z2) står för koordinaterna för punkten på ytan, för att bestämma avståndet mellan båda punkterna.

4. Vet att i allmänhet, r = √((x2 - X1) + (y2 - y1) + (z2 - z1)). I en sfär är varje punkt på ytan på samma avstånd från sfärens mitt. Låt oss ta ovanstående tredimensionella avståndsformel och ersätta variabeln "d" av variabeln "r" av radien får vi en ekvation som gör att vi kan hitta radien vid ett givet centrum (x1,y1,z1) och någon motsvarande punkt på ytan (x2,y2,z2).
Tips
- Ordningen på verksamheten har betydelse. Om du inte är säker på hur matematikreglerna fungerar och din miniräknare stöder parenteser, se till att du använder dem.
- Den här artikeln skapades för att det här ämnet var mycket efterfrågat. Men om du försöker förstå rumslig geometri för första gången är det förmodligen bättre att börja med den andra sidan: att beräkna egenskaperna för en sfär när dess radie är given.
- Pi eller π är en grekisk bokstav som anger förhållandet mellan en cirkels diameter och dess omkrets. Det är ett irrationellt tal och kan inte skrivas som ett förhållande mellan reella tal. Det finns många approximationer, och 333/106 ger pi till fyra decimaler. Idag minns de flesta människor ungefär 3,14 som vanligtvis är tillräckligt korrekt för vardagliga ändamål.
"Beräknar radien för en sfär"
Оцените, пожалуйста статью