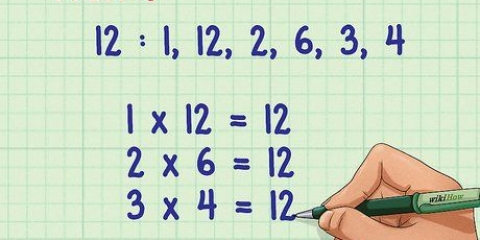Instrucțiuni gratuite pas cu pas 
3x + 2x - 8 
6x + 13x + 6 
8x + 10x + 2 
27x - 12 = 0 
x + 4x + 1 = 0 
y = x − x − 2 
Om du inte kan se var parabeln skär x-axeln, tryck på [2nd] och sedan [TRACE]. Tryck på [2] eller välj "noll-". Flytta markören till vänster om en korsning och tryck på [ENTER]. Flytta markören till höger sida av en korsning och tryck på [ENTER]. Flytta markören så nära korsningen som möjligt och tryck på [ENTER]. Kalkylatorn visar x-värdet.Gör samma sak för den andra skärningspunkten. 
Factoring andragradsekvationer
Ett polynom innehåller en variabel (x) upphöjd till en viss potens, och flera termer och/eller konstanter. För att faktorisera ett polynom måste du dela upp uttrycket i mindre uttryck som multipliceras med varandra. Detta kräver en viss nivå av matematik och kan därför vara svårt att förstå om du inte är så långt ännu.
Steg
Metod 1 av 7: Komma igång
1. Ekvationen. Standardformatet för en andragradsekvation är:
ax + bx + c = 0
Börja med att ordna termerna i din ekvation från högsta till lägsta potens. Ta till exempel:
6 + 6x + 13x = 0
Vi kommer att ordna om det här uttrycket för att göra det lättare att arbeta med – helt enkelt genom att flytta runt termerna:
6x + 13x + 6 = 0
Börja med att ordna termerna i din ekvation från högsta till lägsta potens. Ta till exempel:
Vi kommer att ordna om det här uttrycket för att göra det lättare att arbeta med – helt enkelt genom att flytta runt termerna:
2. Hitta faktorerna med någon av metoderna nedan. Att faktorisera polynomet kommer att resultera i två mindre uttryck som kan multipliceras tillsammans för att få det ursprungliga polynomet:
6x + 13x + 6 = (2x + 3)(3x + 2)
I det här exemplet är (2x +3) och (3x + 2) faktorer från det ursprungliga uttrycket, 6x + 13x + 6.
I det här exemplet är (2x +3) och (3x + 2) faktorer från det ursprungliga uttrycket, 6x + 13x + 6.
3. Kontrollera ditt arbete! Multiplicera de faktorer du hittade. Kombinera liknande termer och du är klar. Börja med:
(2x + 3)(3x + 2)
Låt oss testa detta genom att multiplicera termerna med EBBL (första - yttre - inre - sist), vilket ger oss:
6x + 4x + 9x + 6
Nu lägger vi ihop 4x och 9x eftersom dessa är lika termer. Vi vet att faktorerna är korrekta eftersom vi får tillbaka ekvationen vi började med:
6x + 13x + 6
Låt oss testa detta genom att multiplicera termerna med EBBL (första - yttre - inre - sist), vilket ger oss:
Nu lägger vi ihop 4x och 9x eftersom dessa är lika termer. Vi vet att faktorerna är korrekta eftersom vi får tillbaka ekvationen vi började med:
Metod 2 av 7: Trial and Error
Om du har ett ganska enkelt polynom kan du kanske direkt se vilka faktorerna är. Till exempel, efter lite övning, kan många matematiker se att uttrycket 4x + 4x + 1 har faktorerna (2x + 1) och (2x + 1) bara för att de har sett detta så många gånger. (Detta kommer naturligtvis inte att vara så lätt med mer komplicerade polynom.) Låt oss ta ett mindre standarduttryck för detta exempel:
1. Skriv ner faktorerna för a termen och den c termin. Använd formatet ax + bx + c = 0, känna igen a och c villkor och notera vilka faktorer som finns. För 3x + 2x - 8 betyder detta:
a = 3 och har 1 par faktorer: 1 * 3
c = -8 och den har 4 par av faktorer: -2 * 4, -4 * 2, -8 * 1 och -1 * 8.
2. Skriv två par parenteser med ett tomt mellanslag. Här anger du konstanterna för varje uttryck:
( x )( x )
3. Fyll utrymmet framför x:en med några möjliga faktorer av a där den. För a term i vårt exempel, 3x, finns det bara en möjlighet:
(3x)(1x)
4. Fyll i de två fälten efter x:en med några faktorer för konstanterna. Anta att vi väljer 8 och 1. Ange detta:
(3x 8)(X 1)
5. Bestäm vilka tecken (plus eller minus) som ska placeras mellan x-variablerna och talen. Beroende på tecknen på det ursprungliga uttrycket är det möjligt att ta reda på vad tecknen för konstanterna ska vara. Låt oss ta de två konstanterna för de två faktorerna h och k att nämna:
Om ax + bx + c så (x + h)(x + k)
Om ax - bx - c eller axe + bx - c så (x - h)(x + k)
Om ax - bx + c så (x - h)(x - k)
I vårt exempel, 3x + 2x - 8, är tecknet:(x - h)(x + k), vilket ger oss följande två faktorer:
(3x + 8) och (x - 1)
I vårt exempel, 3x + 2x - 8, är tecknet:(x - h)(x + k), vilket ger oss följande två faktorer:
6. Testa ditt val med första-yttre-inre-sista multiplikationen. Ett snabbt första test för att se om mellantermen är åtminstone rätt värde. Om inte, så har du förmodligen fel c valda faktorer. Låt oss testa svaret:
(3x + 8)(x - 1)
Genom multiplikation får vi:
3x - 3x + 8x - 8
Förenkla detta uttryck genom att lägga till liknande termer (-3x) och (8x), och vi får:
3x - 3x + 8x - 8 = 3x + 5x - 8
Vi vet nu att vi tog fel faktorer:
3x + 5x - 8 3x + 2x - 8
Genom multiplikation får vi:
Förenkla detta uttryck genom att lägga till liknande termer (-3x) och (8x), och vi får:
Vi vet nu att vi tog fel faktorer:
7. Byt dina val om det behövs. I vårt exempel, låt oss prova 2 och 4, istället för 1 och 8:
(3x + 2)(x - 4)
Nu vår c term lika med -8, men den yttre/inre produkten av (3x * -4) och (2 * x) är -12x och 2x, vilket inte är det korrekta b term eller +2x får.
-12x + 2x = 10x
10x 2x
Nu vår c term lika med -8, men den yttre/inre produkten av (3x * -4) och (2 * x) är -12x och 2x, vilket inte är det korrekta b term eller +2x får.
8. Vänd ordningen om det behövs. Låt oss försöka vända 2 och 4:
(3x + 4)(x - 2)
Nu vår c term (4 * 2 = 8) och fortfarande OK, men de yttre/inre produkterna är -6x och 4x.Genom att kombinera dessa får vi:
-6x + 4x = 2x
2x -2x Vi kommer ganska nära 2x där vi vill vara, men skylten är inte rätt än.
Nu vår c term (4 * 2 = 8) och fortfarande OK, men de yttre/inre produkterna är -6x och 4x.Genom att kombinera dessa får vi:
9. Dubbelkolla dina karaktärer om det behövs. Vi behåller denna ordning, men byter ut den med minustecknet:
(3x - 4)(x + 2)
Nu den c term fortfarande ok, och de yttre/inre produkterna är nu (6x) och (-4x). Eftersom:
6x - 4x = 2x
2x = 2x Vi ser nu det positiva 2x tillbaka från det ursprungliga problemet. Det måste vara de rätta faktorerna.
Nu den c term fortfarande ok, och de yttre/inre produkterna är nu (6x) och (-4x). Eftersom:
Metod 3 av 7: Nedbrytning
Denna metod ger alla möjliga faktorer av a och c termer och använd dem för att ta reda på vilka faktorer som är korrekta. Om siffrorna är mycket stora, eller om gissningen av andra metoder kommer att ta för lång tid, använd det här sättet. Ett exempel:
1. Multiplicera a termin med c termin. I det här exemplet,, a är 6 och c är också 6.
6 * 6 = 36
2. Hitta b term genom faktorisering och testning. Vi letar efter 2 siffror som är faktorer av a * c , och tillsammans b term (13) form.
4 * 9 = 36
4 + 9 = 13
3. Ersätt de två talen du får i din ekvation med summan av b termin. Låt oss k och h för att representera de två talen vi har, 4 och 9:
ax + kx + hx + c
6x + 4x + 9x + 6
4. Faktorisera polynomet genom att gruppera. Organisera ekvationen så att du kan isolera den största gemensamma delaren av de två första termerna och de två sista termerna. Båda faktorerna bör vara desamma. Lägg till GCD:erna och placera dem inom parentes, bredvid faktorerna; som ett resultat får du två faktorer:
6x + 4x + 9x + 6
2x(3x + 2) + 3(3x + 2)
(2x + 3)(3x + 2)
Metod 4 av 7: Triple Play
Liknar nedbrytningsmetoden. "Triple play"-metoden undersöker de möjliga faktorerna för produkten av a och c och använd den för att ta reda på vad b måste vara. Ta ekvationen som ett exempel:
1. Multiplicera a termin med c termin. Liksom med nedbrytningsmetoden använder vi denna för att bestämma kandidaterna för b termin. I det här exemplet: a är 8 och c är 2.
8 * 2 = 16
2. Hitta de 2 siffrorna med detta nummer som produkt och med en summa lika med b termin. Detta steg är likvärdigt med nedbrytningsmetoden – vi testar kandidater för konstanterna. Produkten av a och c villkor är 16, och c term är 10:
2 * 8 = 16
8 + 2 = 10
3. Ta dessa 2 siffror och ersätt dem i "triple play"-formeln. Ta de 2 siffrorna från föregående steg - låt oss sätta dem h och k ring dem - och sätt dem i uttrycket:
((ax + h)(ax + k))/ a
Med detta får vi:
((8x + 8)(8x + 2)) / 8
Med detta får vi:
4. Se vilken av de två termerna i nämnaren som kan delas helt med a. I det här exemplet tittar vi på om (8x + 8) eller (8x + 2) kan delas med 8. (8x + 8) är delbart med 8, så vi dividerar denna term med a och låt oss lämna den andre ifred.
(8x + 8) = 8(x + 1)
Termen vi har behållit här är den som blir över efter att ha dividerat med a term:(x + 1)
Termen vi har behållit här är den som blir över efter att ha dividerat med a term:(x + 1)
5. Ta den största gemensamma divisorn (gcd) av endera eller båda termerna, om möjligt. I det här exemplet ser vi att den andra termen har en gcd på 2, eftersom 8x + 2 = 2(4x + 1). Kombinera detta svar med termen du upptäckte i föregående steg. Dessa är faktorerna i din ekvation.
2(x + 1)(4x + 1)
Metod 5 av 7: Skillnaden mellan två kvadrater
Vissa koefficienter i ett polynom kan kännas igen som "kvadrater" eller också som produkten av 2 av samma tal. Genom att ta reda på vad dessa kvadrater är kan du kanske faktorisera polynomen mycket snabbare. Vi tar ekvationen:
1. Ta bort gcd från ekvationen, om möjligt. I det här fallet ser vi att 27 och 12 båda är delbara med 3, så vi kan sätta dem separat:
27x - 12 = 3(9x - 4)
2. Bestäm om koefficienterna för din ekvation är kvadrater. För att använda denna metod är det nödvändigt att kunna bestämma roten till termerna. (Observera att vi har utelämnat decimaler - eftersom dessa tal är kvadrater kan de vara produkten av 2 negativa tal)
9x = 3x * 3x och 4 = 2 * 2
3. Med hjälp av kvadratroten du bestämt kan du nu skriva ut faktorerna. Vi tar a och c värden från föregående steg: a = 9 och c = 4, så rötterna till detta är: - √a = 3 ochc = 2. Dessa är koefficienterna för de faktoriserade uttrycken:
27x - 12 = 3(9x - 4) = 3(3x + 2)(3x - 2)
Metod 6 av 7: ABC-formeln
Om ingenting verkar fungera och du inte kan faktorisera ekvationen, använd abc-formeln. Ta följande exempel:
1. Fyll i motsvarande värden i abc-formeln:
x = -b ± √(b - 4ac)
---------------------
2a
Vi får nu uttrycket:
x = -4 ± √(4 - 4•1•1) / 2
---------------------
2a
Vi får nu uttrycket:
2. Lös för x. Du bör nu få 2 värden för x. Dessa är:
x = -2 + √(3) eller x = -2 - √(3)
x = -2 + √(3) eller x = -2 - √(3)
3. Använd värdena på x för att bestämma faktorerna. Fyll i x-värdena som erhålls i de två ekvationerna, som konstanter. Det här är dina faktorer. Om vi svarar på de två h och k sedan skriver vi de två faktorerna så här:
(x - h)(x - k)
I det här fallet är det slutliga svaret:
(x - (-2 + √(3))(x - (-2 - √(3)) = (x + 2 - √(3))(x + 2 + √(3))
I det här fallet är det slutliga svaret:
Metod 7 av 7: Använd en miniräknare
Om det är tillåtet (eller krävs) att använda en grafräknare, gör detta faktorisering mycket enklare, särskilt under tentor och tentor. Följande instruktioner är för en TI-grafräknare. Vi använder ekvationen från exemplet:
1. Skriv in ekvationen i din miniräknare. Du kommer att använda ekvationslösaren, även känd som skärmen [Y = ].
2. Rita upp ekvationen med kalkylatorn. När du har skrivit in ekvationen, tryck på [GRAPH] - du bör nu se en böjd linje, en parabel som en grafisk representation av din ekvation (och det är en parabel, eftersom vi har att göra med ett polynom).
3. Hitta var parabeln skär x-axeln. Eftersom en andragradsekvation traditionellt noteras som ax + bx + c = 0, är dessa två x-värden som gör ekvationen lika med noll:
(-1, 0), (2, 0)
x = -1, x = 2
4. Ange x-värdena du fick, i de två faktoriserade uttrycken. Om vi tar de två x-värdena h och k skriv ner det som en term, så ser uttrycket vi använder ut så här:
(x - h)(x - k) = 0
Så våra två faktorer blir då:
(x - (-1))(x - 2) = (x + 1)(x - 2)
Så våra två faktorer blir då:
Tips
- Om du faktoriserade polynomet med abc-formeln, och ditt svar innehåller rötter, kan du konvertera x-värdena till bråk för att kontrollera dem.
- Om en term inte har någon koefficient framför sig, så är koefficienten lika med 1, t.ex. x = 1x.
- Om du har en TI-84 miniräknare finns det ett program som heter SOLVER som kan lösa en andragradsekvation åt dig. Detta löser också högre grad av polynom.
- Efter mycket träning kommer du så småningom att lyckas lösa polynom utantill. Men bara för att vara säker är det bättre att alltid skriva ut dem.
- Om en term inte finns är koefficienten lika med noll. Då kan det vara användbart att skriva om ekvationen. T.ex. x + 6 = x + 0x + 6.
Varningar
- När du lär dig det här konceptet i mattelektionen, var uppmärksam på vad läraren förklarar och använd inte bara din egen favoritmetod. Du kan bli ombedd att använda en specifik metod på ett test, eller så är det inte säkert att grafräknare är tillåtna.
Förnödenheter
- Penna
- Papper
- Andragradsekvation (även kallad andragradsekvation)
- Grafräknare (valfritt)
"Factoring andragradsekvationer"
Оцените, пожалуйста статью
