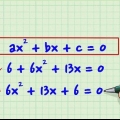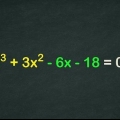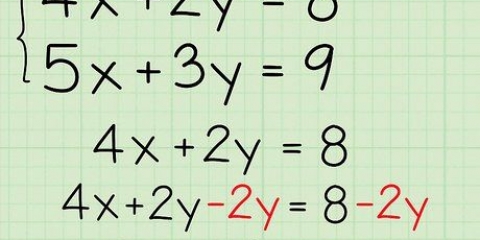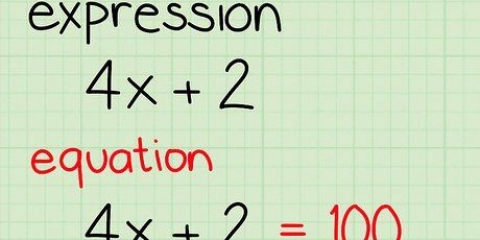Till exempel kan variabeln 12y skrivas om som produkten av faktorerna 12 och y. Vi kan skriva 12y som 3(4y), 2(6y), etc., med hjälp av faktorerna 12 som är mest bekväma. Vi kan till och med gå så långt som 12 år flera gånger upplösa. Med andra ord, vi behöver inte stanna vid 3(4y) eller 2(6y) - vi kan faktorisera 4y och 6y till 3(2(2y) respektive 2(3(2y)). Tydligen är dessa två uttryck likvärdiga med varandra. 
Låt oss prova ett exempelproblem. För att faktorisera ekvationen 12x + 6, letar vi först efter gcd för 12x och 6. 6 är det största talet som delar både 12x och 6, så vi kan förenkla ekvationen till 6(2x + 1). Denna process gäller även ekvationer som involverar negativa tal och bråk. x/2 + 4, till exempel, kan förenklas till 1/2(x + 8) och -7x + -21 kan faktoriseras till -7(x + 3). 

Ta till exempel andragradsekvationen x + 5x + 6 = 0. Eftersom 3 x 2 = 6 och 3 + 2 = 5, blir den förenklade ekvationen (x + 3)(x + 2). Små variationer på denna enkla snabbfix kan hittas i själva ekvationen: Om andragradsekvationen har formen x-bx+c, kommer ditt svar att se ut så här: (x - _)(x - _). Om du har formen x+bx+c, kommer ditt svar att se ut så här: (x + _)(x + _). Om du har formen x-bx-c kommer ditt svar att se ut så här: (x + _)(x - _). Obs: De tomma fälten kan vara bråktal eller decimaler. Till exempel, ekvationen x + (21/2)x + 5 = 0 faktorer in i (x + 10)(x + 1/2). 
Låt oss arbeta fram en exempeluppgift. 3x - 8x + 4 verkar lite skrämmande till en början. Men om vi inser att 3 bara har två faktorer (3 och 1), så blir det mycket lättare, eftersom vi vet att vårt svar måste ha formen (3x +/- _)(x +/- _). I det här fallet kommer att ge rätt svar om du anger -2 i de tomma fälten. -2 × 3x = -6x och -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, så vi ser att termerna räknade inom parentes multiplicerade tillsammans, har den ursprungliga ekvationen som produkt. 
Till exempel, ekvationen x + 6x + 9 uppfyller denna form. 3 är 9 och 3 × 2 är 6. Så vi vet att faktorerna i denna ekvation är lika med (x + 3)(x + 3) eller (x + 3). 
Låt oss återgå till ekvationen x + 5x + 6 = 0. Den lösta ekvationen är (x + 3)(x + 2) = 0. Om en av dessa faktorer är lika med 0, är hela ekvationen 0, så de möjliga svaren för x är de siffror där (x + 3) och (x + 2) är lika med 0. Dessa siffror är -3 respektive -2. 
Vi tillämpar -2 och -3 på x + 5x + 6 = 0. Först ut: -2: (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. Detta är korrekt, så -2 är ett giltigt svar. Nu försöker vi -3: (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Detta är också korrekt, så -3 är också ett giltigt svar. 

Ekvationen 4x + 8xy + 4y kan skrivas om till 4x + (2 × 2 × 2)xy + 4y. Nu blir det tydligt att den är i rätt form, så att vi med viss säkerhet kan konstatera att vår ekvation kan inkluderas i (2x + 2y). 
Till exempel: 8x - 27y kan inkluderas i (2x - 3y)(4x + ((2x)(3y)) + 9y).
Faktoreringsekvationer
I matematik är det så faktorisera bestämma tal eller uttryck som, när de multipliceras tillsammans, ger ett visst värde eller ekvation. Factoring är en användbar färdighet att lära sig när man löser enkla matematiska problem; förmågan att faktorisera korrekt blir nästan avgörande när man hanterar andragradsekvationer och andra polynom. Factoring kan användas för att förenkla enkla matematiska ekvationer för att göra det lättare att lösa dem. Factoring kan göra att du själv kan utesluta möjliga svar mycket snabbare än om du var tvungen att kontrollera var och en av dem.
Steg
Metod 1 av 3: Faktorisering av tal och enkla ekvationer

1. Förstå definitionen av factoring i siffror. Factoring är i princip enkelt, men i praktiken kan det vara ganska utmanande när man löser komplexa ekvationer. Därför är det enklaste tillvägagångssättet att börja med små tal och sedan enkla ekvationer innan du går vidare till mer avancerade applikationer. De faktorer av ett givet tal är de tal som, multiplicerade tillsammans, ger det enda talet. Till exempel är faktorerna för 12 1, 12, 2, 6, 3 och 4, eftersom 1 × 12, 2 × 6 och 3 × 4 alla har 12 som produkt.
- Ett annat sätt att tänka på detta är att faktorerna för ett givet tal är de siffror som gör talet in kan delas i sin helhet.
- Kan du hitta alla faktorer på 60? Vi använder siffran 60 för olika applikationer (antal minuter i en timme, sekunder i en minut, etc.) eftersom det är delbart med en stor uppsättning tal.
- Faktorerna 60 är 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 och 60.

2. Förstå att ekvationer också kan faktoriseras. Precis som siffror kan variabler med koefficienter också faktoriseras. Det gör du genom att hitta faktorerna för variabelns koefficient. Att veta hur man faktoriserar variabler är till hjälp för att förenkla ekvationer som variablerna är en del av.

3. Tillämpa den fördelande egenskapen för multiplikation på faktorisering av matematiska ekvationer. Med hjälp av dina kunskaper om hur du faktorisera både vanliga tal och variabler med koefficienter, kan du också förenkla matematiska ekvationer genom att bestämma de faktorer som är gemensamma för tal och variabler i en matematisk ekvation. Vanligtvis kommer vi att förenkla ekvationen så långt som möjligt genom att leta efter den största gemensamma divisorn (gcd). Denna förenklingsprocess är möjlig på grund av multiplikationsfördelningsegenskapen, som säger att för alla tal a, b och c, a(b + c) = ab + ac.
Metod 2 av 3: Faktorisering av andragradsekvationer

1. Se till att ekvationen är i kvadratisk form (ax + bx + c = 0). andragradsekvationer har formen ax + bx + c = 0, där a, b och c är numeriska konstanter och a inte är lika med 0 (observera att a är lika med burk är på 1 eller -1). Om du har att göra med en ekvation med en variabel (x) och en eller flera termer av x i kvadrat, kan du vanligtvis byta termerna i ekvationen med en vanlig matematisk operation för att få 0 på ena sidan av ekvationen. tecken och yxa osv. å andra sidan.
- Till exempel har du följande matematiska ekvation: 5x + 7x - 9 = 4x + x - 18 som kan förenklas till x + 6x + 9 = 0, i kvadratisk form.
- Ekvationer med större potenser av x, som x, x, etc. är inte andragradsekvationer. Dessa är kubikekvationer eller högre, om inte ekvationen kan förenklas så att termer med högre potens av x(än kvadrater) elimineras.

2. I andragradsekvationer där a = 1, räknar du in i (x+d )(x+e), där d × e = c och d + e = b. Om din andragradsekvation har formen x + bx + c = 0 (med andra ord, om koefficienten för x = 1), så är det möjligt (men inte säkert) att en relativt enkel genväg kan användas för att faktorisera ekvationen. Hitta två tal som båda har c som produkt och lägg ihop dem för att få b som en summa. Om du har dessa två siffror d och e, sätt dem i följande uttryck: (x+d)(x+e). Dessa två termer, när de multipliceras, ger dig andragradsekvationen - med andra ord, de är faktorerna i din andragradsekvation.

3. Om möjligt kan du också lösa upp faktorerna genom att bara titta noga. Tro det eller ej, du kan lösa enkla andragradsekvationer bara genom att titta på problemet noggrant och sedan väga de möjliga svaren tills du hittar det rätta. Med andra ord, bryts ner i faktorer genom att prova. Om ekvationen har formen ax+bx+c och a>1, då kommer termerna att ha formen (dx +/- _)(ex +/- _), där d och e är konstanter, större än noll, som multiplicerat med a som produkt. Både d och e (eller båda) burk lika med 1, men det är inte alltid så. Om båda är 1, har du i huvudsak använt den snabba metoden som beskrivs ovan.

4. Lös detta genom att kvadrera. I vissa fall kan andragradsekvationer faktoriseras snabbt och enkelt genom att använda en speciell matematisk egenskap. Alla andragradsekvationer av formen x + 2xh + h = (x + h). Så om värdet för b i din ekvation är dubbelt så stort som kvadratroten av c, så kan din ekvation faktoriseras till (x + (sqrt(c))).

5. Använd faktorer för att lösa andragradsekvationer. Oavsett hur du faktorisera en andragradsekvation; när den väl har räknats in kan du hitta de möjliga svaren för värdet för x genom att sätta varje faktor lika med noll och lösa för det. Eftersom du letar efter värden för x där din ekvation är noll, kommer ett värde för x som gör endera faktorn lika med noll att vara det möjliga svaret på din andragradsekvation.

6. Kontrollera dina svar – några av dem kan vara felaktiga! När du har hittat de möjliga svaren för x, tillämpa dem tillbaka på din ursprungliga ekvation för att se om de är giltiga. Ibland kommer svaren du hittar att vara den ursprungliga ekvationen inte gör lika med noll när du tillämpar dem. Dessa svar är felaktig och vi ignorerar dem.
Metod 3 av 3: Factoring av andra former av ekvationer

1. Om ekvationen har formen a-b, är de faktoriserade termerna (a+b)(a-b). Ekvationer för två variabler löses annorlunda än andragradsekvationer. För alla ekvationer a-b där a och b inte är lika med 0, är ekvationens faktorer (a+b)(a-b).
- Till exempel, ekvationen 9x - 4y = (3x + 2y)(3x - 2y).

2. Om ekvationen har formen a+2ab+b, sönderdela den i (a+b). Notera: med a trinomial av formen a-2ab+b, den upplösta formen är något annorlunda: (a-b).

3. Om ekvationen har formen a-b, sönderdelar du den till (a-b)(a+ab+b). Slutligen bör det nämnas att även kubikekvationer och högre polynom kan faktoriseras, även om denna process snabbt blir obearbetat komplicerad.
Tips
- a-b kan faktoriseras, men a+b kan inte.
- Lär dig att faktorisera konstanter – detta kan hjälpa.
- Se upp för bråk under faktorisering och räkna ut dem korrekt och noggrant.
- Om du har ett trinomium av formen x+bx+ (b/2), så är den faktoriserade formen (x+(b/2)) (du kan stöta på detta med en kvadratformel).
- Kom ihåg att a x 0 = 0.
Förnödenheter
- Papper
- Penna
- Matematikbok (om det behövs)
"Faktoreringsekvationer"
Оцените, пожалуйста статью