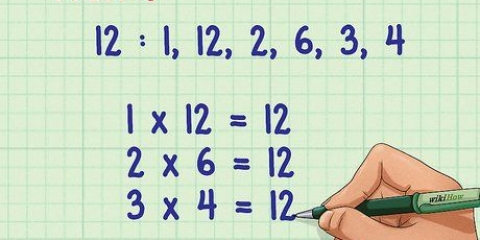Faktorering av ett tal: 11 steg (med bilder)

Steg
- Metod 1 av 2: Factoring heltal
- Metod 2 av 2: Big Number Factoring-strategi
Tips
Varningar
Förnödenheter

Faktorerna för ett givet produktnummer är de siffror som, när de multipliceras tillsammans, ger den produkten. Ett annat sätt att tänka på detta är att varje tal är produkten av flera faktorer. Att lära sig att faktorisera är en viktig matematisk färdighet, som inte bara används inom aritmetik, utan också inom algebra, analys och andra matematiska områden. Läs vidare för att lära dig mer om faktorisering!

Steg

Metod 1 av 2: Factoring heltal

1. Skriv ner numret. Du kan faktorisera vilket tal som helst, men för enkelhetens skull börjar vi med ett heltal. Heltal är positiva eller negativa tal utan bråktal eller decimaler.

ta numret 12. Skriv detta på ett papper.

2. Hitta ytterligare två tal som multiplicerat tillsammans bildar det första talet som en produkt. Vilket heltal som helst kan skrivas som produkten av två andra heltal. Även primtal kan skrivas som produkten av 1 och själva primtalet. Att tänka i termer av faktorer kräver ett annat sätt att resonera. Du frågar dig faktiskt, "vilken multiplikation är lika med detta tal?"

I vårt exempel har 12 flera faktorer - 12 × 1, 6 × 2 och 3 × 4 - alla är lika med 12. Så det kan vi säga 1, 2, 3, 4, 6 och 12 är alla faktorer av 12. För vårt syfte räcker det att fortsätta med faktorerna 6 och 2.

Jämna tal är särskilt lätta att faktorisera, eftersom dessa tal alltid har en faktor på 2. 4 = 2 × 2, 26 = 13 × 2, etc.

3. Bestäm om de valda faktorerna kan lösas upp igen själva. Många siffror – särskilt de större – kan faktoriseras flera gånger. Beroende på situationen kan du eller kanske inte dra nytta av detta.

Till exempel räknade vi in 12 till 2 × 6. Observera att 6 återigen kan räknas in i faktorerna 3 × 2 = 6. Så vi kan säga att 12 = 2×(3×2).

4. Sluta factoring när du stöter på en primfaktor. Primtal är tal som är delbara med 1 och sig själva. Till exempel 1, 2, 3, 5, 7, 11, 13 och 17 är alla primtal. Om du har faktoriserat ett tal till den punkt där det bara finns primtal kvar, är det ingen idé att fortsätta, eftersom de enda faktorerna som är kvar är 1 och själva primtalet.

I vårt exempel löste vi upp 12 och förenklade det till 2 × (2 × 3). 2, 2 och 3 är alla primtal. Om vi skulle gå ännu längre skulle vi behöva faktorisera (2 × 1) × ((2 × 1)(3 × 1)), vilket inte längre är till någon nytta för dig..

5. Lös negativa tal på samma sätt. Negativa tal kan faktoriseras på nästan samma sätt som positiva tal. Den stora skillnaden är att faktorerna multiplicerade tillsammans måste få ett negativt tal som produkt, så ett udda antal av faktorerna måste vara negativt.

Låt oss ta faktor 60 som ett exempel. Titta vidare nedan:

-60 = -10 × 6

-60 = (-5 × 2) × 6

-60 = (-5 × 2) × (3 × 2)

-60 = -5×2×3×2. Observera att att ha ett udda antal negativa tal bredvid 1:an returnerar samma produkt. Till exempel, -5 × 2 × -3 × -2 är också lika med 60.

Metod 2 av 2: Big Number Factoring-strategi

1. Skriv ditt nummer överst i en tabell med 2 kolumner. Även om det vanligtvis är väldigt lätt att faktorisera mindre siffror, kan ibland större siffror vara ganska skrämmande. De flesta av oss skulle ha svårt att ta hänsyn till ett 4- eller 5-siffrigt nummer med bara din hjärna. Som tur är blir detta mycket enklare med hjälp av ett bord.

Välj ett 4-siffrigt nummer att faktorisera - 6552.

2. Dividera ditt tal med minsta möjliga primtal, förutom 1. Skriv primtalet i den vänstra kolumnen och svaret i nästa kolumn. Som beskrivits ovan är jämna tal lättast att faktorisera eftersom det minsta primtalet (förutom 1) alltid är lika med 2. Udda tal har å andra sidan olika minsta primtalsfaktorer.

I vårt exempel vet vi att 2 är den minsta primfaktorn, eftersom 6552 är ett jämnt tal. 6552 2 = 3276. I den vänstra kolumnen skriver vi 2 och till höger 3276.

3. Fortsätt faktoriseringen på detta sätt. Faktorera nu talet i den högra kolumnen och hitta den minsta primfaktorn av detta tal. Skriv det under föregående primtal i den vänstra kolumnen och det nya talet i den högra kolumnen. Fortsätt så här tills du inte kan lösa längre (talet i högerspalten blir mindre och mindre).

Så för att fortsätta vårt exempel: 3276 ÷ 2 = 1638, så i den vänstra kolumnen skriver vi en till 2 och i högerspalten 1638. 1638 ÷ 2 = 819, så vi skriver 2 och 819 i vänster och höger kolumn.

4. Behandla de udda talen genom att alltid börja med de minsta primtalsfaktorerna. För udda tal kan det minsta primtalet skilja sig, till skillnad från jämna tal där 2 alltid är det minsta primtal (förutom 1). Börja med primtalsfaktorer som 3, 5, 7, 11 och så vidare tills du hittar en som är en faktor av ditt tal. Detta är den minsta primfaktorn.

I vårt exempel ser vi att 819 är udda och därför inte kan ha en primtalsfaktor på 2. Så låt oss prova en annan prime. 819 ÷ 3 = 273 utan rest, så 3 är den minsta primfaktorn av 819 och vi fortsätter med 273.

När du letar efter faktorer, prova alla primtal upp till kvadratroten av den största faktorn du hittade. Om inget av talen du försöker är en divisor av den största faktorn, så är den största divisorn i sig förmodligen primtal, så du är klar med att faktorisera.

5. Fortsätt tills du kommer till 1. Fortsätt att hitta den minsta primtalsfaktorn av talen i den högra kolumnen tills du står kvar med ett primtal i den högra kolumnen. Detta delar du sedan med sig själv, så att siffran visas i den vänstra kolumnen och en "1" i den högra kolumnen.

Låt oss nu avsluta nedbrytningen. se nedan för detaljer:

Dividera igen med 3: 273 ÷ 3 = 91, ingen rest, så vi skriver 3 och 91.

Låt oss prova en 3 igen: det här fungerar inte för 91, och det fungerar inte med 5 (nästa primtal), men 91 ÷ 7 = 13 fungerar, utan rest, så vi skriver ner 7 och 13.

Låt oss försöka 7 igen: 13 har varken 7 eller 11 som en faktor, utan sig själv: 13 ÷ 13 = 1.Så för att stänga det här bordet, noterar vi 13 och 1. Vi kan äntligen sluta factoring.

6. Siffrorna i den vänstra kolumnen är dina faktorer. Det betyder att produkten av en multiplikation av dessa tal måste vara lika med talet överst i tabellen. Om samma faktor förekommer mer än en gång, skriv det som en styrka av den faktorn för att spara utrymme. Till exempel, om 2:an förekommer fyra gånger i din lista över faktorer, skriv den som 2 istället för 2 × 2 × 2 × 2.

Så i vårt exempel skriver vi så här: 6552 = 2×3×7×13. Detta är den fullständiga primfaktoriseringen av 6552. Så produkten av multiplikationen av dessa tal är 6552.

Tips

1:an är inte ett primtal, utan ett specialfall.
De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19 och 23.
Förstå att ett tal är en faktor av ett annat, större tal, om detta tal är helt delbart med faktorn; alltså utan en rest kvar. Till exempel är talet 6 en faktor på 24, eftersom 24 ÷ 6 = 4, utan resterande.6 är därför inte en faktor på 25.
Om siffrorna i täljaren summeras till en multipel av tre, är tre en faktor av det talet. ( 819 = 8+1+9 = 18 = 1+8 =9.Tre är en faktor på nio, så det är också en faktor på 819)
Vissa siffror kan faktoriseras snabbare, men det här sättet fungerar alltid och en extra fördel är att primfaktorerna listas i stigande ordning när du är klar.
Kom ihåg att vi bara pratar om heltal som 1, 2, 3, 4, 5...och inte om bråktal eller decimaltal, vilket ligger utanför den här artikelns räckvidd.

Varningar

Gör det inte för svårt för dig själv. Om du har uteslutit en faktor, fortsätt inte att kolla i det oändliga. När du har upptäckt att 2 inte kan vara en faktor på 819, gå vidare och vet att du inte behöver överväga 2 som en faktor igen.