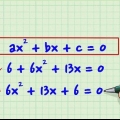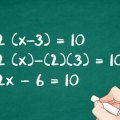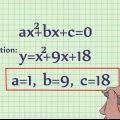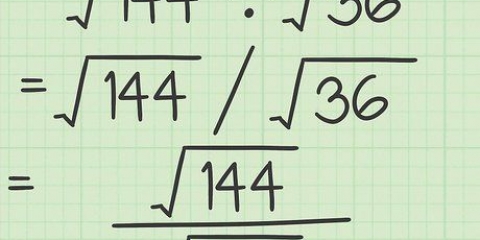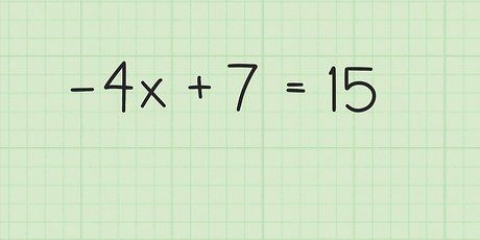Eftersom 3x har ett ändligt antal möjliga faktorer, 3x och x, kan du skriva dessa inom parentes: (3x +/- ? )(x +/-- ?) = 0. Använd sedan en elimineringsmetod där du använder faktorerna 4 för att hitta en kombination som ger -11x som resultat av multiplikationen. Du kan använda antingen en kombination av 4 och 1, eller 2 och 2, eftersom multiplikationen av båda talkombinationerna ger 4. Tänk på att en av termerna måste vara negativ, eftersom termen är -4. Prova (3x +1)(x -4). När du räknar ut detta får du - 3x -12x +x -4. Om du kombinerar termerna -12x och x får du -11x, vilket är den mellanterm du ville komma fram till. Nu har du faktoriserat denna andragradsekvation. Ett annat exempel; vi försöker faktorisera en ekvation som inte fungerar: (3x-2)(x+2) = 3x +6x -2x -4. Om du kombinerar dessa termer får du 3x -4x -4. Även om produkten av -2 och 2 är lika med -4, fungerar inte mellantermen eftersom du letade efter -11x, inte -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Så båda lösningarna fungerar separat och båda är verifierade att fungera och är korrekta i två olika lösningar. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Lös andragradsekvationer
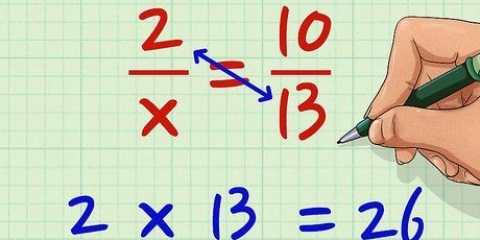
En andragradsekvation är en ekvation där den största exponenten för en variabel är två. Tre av de vanligaste metoderna för att lösa dessa ekvationer är: faktorisering, användning av abc-formeln eller dividering av kvadraten. Om du vill veta hur man behärskar dessa metoder, följ bara dessa steg.
Steg
Metod 1 av 3: Factoring

1. Flytta alla termer till ena sidan av ekvationen. Det första steget i factoring är att flytta alla termer till ena sidan av ekvationen och lämna x positivt. Tillämpa additions- eller subtraktionsoperationen på termerna x, variabeln x och konstanterna, flytta dem till ena sidan av ekvationen på detta sätt och lämna ingenting på den andra sidan. Så här fungerar det:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Faktorera uttrycket. För att faktorisera uttrycket måste du faktorisera faktorerna för 3x och faktorerna för konstanten -4 för att multiplicera dem och sedan addera dem för att ge värdet av mellantermen, -11. Så här gör du det:

3. Bestäm att varje par av parenteser är lika med noll och behandla dem som separata ekvationer. Detta gör att du hittar två värden för x som båda gör hela ekvationen lika med noll. Nu när du har räknat in ekvationen, är det bara att göra varje par parentes lika med noll. Så du kan skriva att: 3x +1 = 0 och x - 4 = 0.

4. Lös varje ekvation. I en andragradsekvation finns två givna värden för x. Lös varje ekvation separat genom att isolera variabeln och skriv resultatet av x. Så här går det till:

5. Kontrollera x = -1/3 tum (3x + 1)(x – 4) = 0:
Vi får (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... genom att ersätta:(-1 + 1)(-4 1/3) ?=? 0 ..... genom att förenkla:(0)(-4 1/3) = 0 ..... genom att multiplicera: så 0=0 ..... Ja, x = -1/3 fungerar
Vi får (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... genom att ersätta:(-1 + 1)(-4 1/3) ?=? 0 ..... genom att förenkla:(0)(-4 1/3) = 0 ..... genom att multiplicera: så 0=0 ..... Ja, x = -1/3 fungerar

6. Kontrollera x = 4 tum (3x + 1)(x - 4) = 0:
Vi får (3[4] + 1)([4] – 4) ?=? 0..... genom att ersätta:(13)(4 – 4) ?=? 0 ..... genom att dämpa:(13)(0) = 0 ..... genom att multiplicera:0=0 ..... Ja, x = 4 fungerar
Vi får (3[4] + 1)([4] – 4) ?=? 0..... genom att ersätta:(13)(4 – 4) ?=? 0 ..... genom att dämpa:(13)(0) = 0 ..... genom att multiplicera:0=0 ..... Ja, x = 4 fungerar
Metod 2 av 3: Tillämpa Abc-formeln

1. Flytta alla termer till ena sidan av ekvationen och slå samman liknande termer. Flytta alla termer till ena sidan av likhetstecknet och behåll termen x positiv. Skriv termerna i fallande storleksordning, så x kommer först följt av x, sedan konstanten. Så här gör du det:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Skriv ner abc-formeln. Detta är: {-b +/-√ (b - 4ac)}/2a

3. Bestäm värdena för a, b och c i andragradsekvationen. Variabeln a är koefficienten för x, b är koefficienten för x och c är konstanten. För ekvationen 3x -5x - 8 = 0, a = 3, b = -5 och c = -8. Skriv ner det här.

4. Ersätt värdena för a, b och c i ekvationen. Nu när du känner till värdena för de tre variablerna kan du bara koppla in dem i ekvationen som vi visar här:

5. Beräkna. Efter att ha fyllt i siffrorna löser du problemet ytterligare. Nedan kan du läsa hur det går vidare:

6. Förenkla kvadratroten. Om talet under det radikala tecknet är en perfekt kvadrat eller också ett kvadrattal, får du ett heltal med kvadratroten. I andra fall, förenkla kvadratroten så mycket som möjligt. Om talet är negativt, och du är säker på att detta är avsikten, blir kvadratroten av talet mindre enkel. I det här exemplet är √(121) = 11. Du kan sedan skriva att x =(5 +/- 11)/6.

7. Lös för positiva och negativa siffror. När du har blivit av med kvadratroten kan du fortsätta tills du hittar negativa och positiva svar för x. Nu när du har (5 +/- 11)/6 kan du skriva ner de två möjligheterna:

8. Lös för de positiva och negativa svaren. Räkna vidare:

9. Förenkla. För att förenkla, dividera svaren med det största talet som är delbart med både täljaren och nämnaren. Så dividera det första bråket med 2 och det andra med 6 och du har löst x.
Metod 3 av 3: Dela kvadraten

1. Flytta alla termer till ena sidan av ekvationen. Se till att a av x är positivt. Så här gör du det:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- I denna ekvation, a lika med 2, b är -12, och c är -9.

2. Flytta konstanten c till andra sidan. Konstanten är det numeriska värdet utan variabel. Flytta den till höger sida av ekvationen:

3. Dividera de två sidorna med koefficienten för a eller x term. Om x inte har någon term framför sig och har en koefficient med värdet 1 kan du hoppa över detta steg. I det här fallet måste du dividera alla termer med 2, så här:

4. Del b två gånger, kvadrera det och lägg till resultaten på båda sidor av tecknet.Deb i detta exempel är -6. Så här gör du:

5. Förenkla båda sidor. Faktorisera termerna till vänster för att få (x-3)(x-3), eller (x-3). Lägg till villkoren till höger för att få 9/2 + 9, eller 9/2 + 18/2, vilket summerar till 27/2.

6. Hitta kvadratroten från båda sidorna. Kvadratroten av (x-3) är helt enkelt (x-3). Du kan också skriva kvadratroten av 27/2 som ±√(27/2). Därför är x - 3 = ±√(27/2).

7. Förenkla kvadratroten och lös x. För att förenkla ±√(27/2), leta efter en perfekt kvadrat eller kvadrattal med siffrorna 27 eller 2 eller i deras faktorer. Kvadratalet 9 kan hittas i 27, eftersom 9 x 3 = 27. För att eliminera 9 från roten, skriv det som en separat rot och förenkla till 3, kvadratroten ur 9. Lämna √3 i täljaren för bråket eftersom det inte kan separeras som en faktor från 27, och gör 2 till nämnaren. Flytta sedan konstanten 3 från vänster sida av ekvationen till höger sida och skriv ner dina två lösningar för x:
Tips
- Som du kan se har det radikala tecknet inte helt försvunnit. Därför slås inte termerna i täljaren samman (de är inte lika termer). Så det är meningslöst att dela upp minus och plus. Istället, genom att dividera, ser vi till att alla gemensamma faktorer försvinner – men "ENDAST" om faktorn är lika för båda konstanterna, "OCH" kvadratrotens koefficient.
Оцените, пожалуйста статью